Fluent两相流分析方法笔记

CFD研究方法需要较少的时间和费用投入，克服了理论分析和实验方法的缺点，具有很高的准确性，所以，在流体动力学研究中，CFD方法 论在发挥越来越重要的作用[1]。

01 欧拉-拉格朗日模型

欧拉-拉格朗日模型是把流体相作为连续相，运用欧拉法创立流体相的连续性、动量以及能量守恒方程。大量的气泡，液滴或者粒子作为离散相，建立离散相的拉格朗日方程。

02欧拉-欧拉模型

Euler-Euler法是将气泡等分散相和液相流体均看作拟连续介质，气泡和流体是共同独立存在的拟流体并且相互之间能够相互渗透，而在Euler坐标系下需要与连续流体相似的控制守恒方程分别对气、液两相进行表示。该模型也被称作双流体模型。Euler-Euler方法在计算量上比Euler-Lagrange法要小的多，FLUENT中有三种Euler-Euler多相流模型：VOF (Volume of Fluid) 模型、混合 (Mixture) 模型和Euler模型。

VOF模型

VOF模型是一种表面追踪方式，该模型以欧拉坐标系为基础。如果要求模拟不相容流体的交界面性质是可选用此模型[2]。通常在FLUENT中应用VOF模型时大部分解决瞬态问题，当然也能应用VOF解决稳态流场问题，如图1所示。此外，用户在使用VOF模型时会受到一定条件的限制：

• 必须使用基于压力求解器。VOF模型不能使用基于密度求解器。
• VOF模型不允许没有流体的空的区域。
• 只能有一相为可压缩理想气体。对于使用UDF所定义的可压缩液体没有限制。
• 不能使用VOF模型模拟顺流向的周期性流动。
• 不能既使用VOF模型，又使用二阶隐式时间步进格式。
• 当使用DPM模型进行并行粒子跟踪时，不能使用共享存储器选项，可以使用消息传递选项。

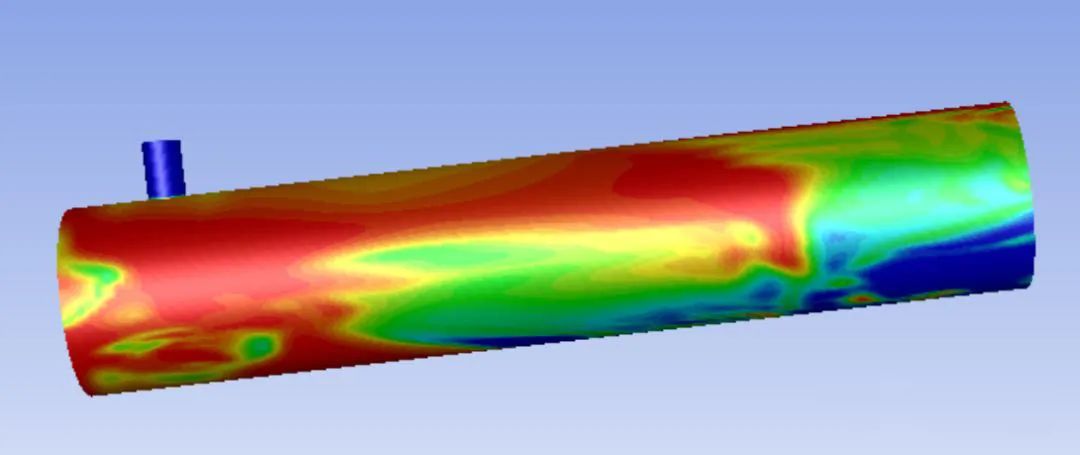
图1 VOF相成分分布

混合模型

混合 (Mixture) 模型是一种被简化了的多相流模型，大多数被用于模拟不同相之间，具有不同速度的多相流动问题，应用混合模型时假设不同相之间存在强耦合的小尺度空间上的局部平衡，如图2所示。在一些情况下，混合模型和欧拉多相流模型是很好的可以相互替代的模型。但是，使用混合模型时会有一定的限制：

• 必须使用基于压力求解器。
• 只有一相可以是可压缩理想气体。
• 流向周期性问题不能采用指定质量流量率方式。
• 不能模拟凝结和熔化。
• 气穴模型和LES湍流模型不能共用。
• 对搅拌区域应用MRF进行处理时，不能采用相对速度公式。
• 不能模拟无粘性流动。
• 不能处理壁面壳导热问题。
• 当使用DPM模型进行并行粒子跟踪时，不能使用共享存储器选项，可以使用消息传递选项。

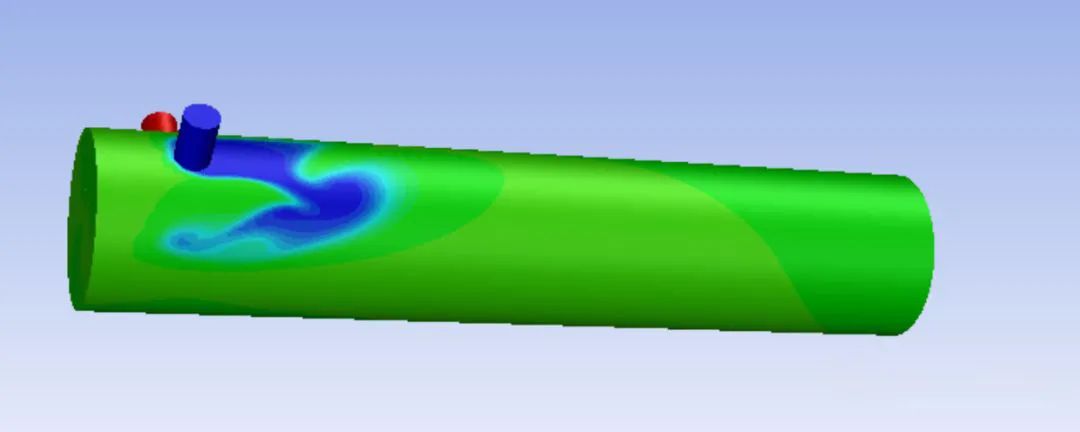
图2 Mixture相成分分布

欧拉模型

欧拉模型用于处理复杂流体运动问题。气泡流问题、上浮问题、颗粒悬问题以及流化床问题等，常常应用欧拉模型来解决，如图3所示。同时，研究者们在应用欧拉多相流模型也存一定的局限：

• 不能将雷诺应力湍流模型施加于各相之间。
• 流体的流向为周期性流动时，不能用欧拉多相流模型。
• 欧拉模型不能仿真凝固和融化过程。
• 欧拉模型不能模拟无粘性流动。

在欧拉-欧拉模型中，假设不同阶段是可以彼此散布的不间断的统一体，相体积不能被其他相所取代，以获得相分数体积的概念。

图3 欧拉相成分分布

03 湍流模型

湍流属于高度非线性的复杂流动，而且通过指定的数值方法对湍流进行数值模拟就可以使模拟结果与实际情况达到基本吻合。本小节将介绍关于湍流的各种数值模拟方法。

湍流模型Spalart-Allmaras模型、Standard k-ε模型、RNG k-ε模型、Realizable k-ε模型、v2-f模型、RSM模型和LES模型这几种，但使用比较多的湍流模型为以下三种：

标准 k-ε模型

标准k-ε模型是由Launder 和Spalding 共同提出。模型本身的稳定性、经济性和相对较高的计算精度，使其成为湍流模型中使用最广泛且最知名的模型。k-ε模型用于求解湍流动能 (k) 方程和湍流耗散率 (ε) 方程，得到k与ε的解，然后通过k与ε的值计算得到湍流粘度。而雷诺应力解是通过Boussinesq假设解得到的。

RNG k-ε模型

RNG k-ε模型在形式上与标准k-ε模型相类似，但是在计算功能上要强于标准k-ε模型，其主要改进措施有：

• 在ε方程中添加了一个附加项，在计算速度梯度较大的流场时可以使精度得到提高。
• 在模型中涉及到了旋转效应，所以在对强旋转流动计算上精度也同样得到了提高。
• 模型中包含计算湍流Prandtl数的公式，而不像标准湍流模型中仅使用用户定义的常数。
• 标准湍流模型是一个高雷诺数模型，RNG k-ε模型在对近壁区进行一定处理后可以进行低雷诺数效应的计算。

• Realizablek-ε模型

Realizable k-ε模型与标准k-ε模型的主要区别是：

• 在Realizable k-ε模型中使用了新的湍流粘度公式。
• ε方程是通过涡量扰动量均方根的输运方程推导出来的。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删