Matlab基础操作入门教程

Matlab

一、matlab使用基础

1.1 通用命令

1.1.1 通用命令

命令	说明	命令	说明
cd	显示或改变当前工作目录	load	加载指定文件的变量
dir	显示当前目录或指定目录下的文件	diary	日志文件命令
clc	清除工作窗中的所有显示内容	！	调用dos命令
home	将光标移至命令窗口的最左上角	exit	退出matlab
clf	清除图形窗口	quit	退出matlab
type	显示文件内容	pack	收集内存碎片
clear	清理内存变量	hold	图形保持开关
echo	工作窗信息显示开关	path	显示搜索目录
disp	显示变量或文字内容	save	保存内存变量到指定文件

1.1.2 输入内容的编辑

键盘按键	说明	键盘按键	说明
↑	调用上一行	Home	光标置于当前行开头
←	光标左移一个字符	End	光标置于当前行末尾
→	光标右移一个字符	Esc	清除当前输入行
Ctrl+←	光标左移一个单词	Del	删除光标处的字符
Ctrl+→	光标右移一个单词	Backspace	删除光标前的字符
Alt+Backspace	恢复上一次删除

1.1.3 标点

标点	标点
:	%
;	!
,	=
( )	’
[ ]	.
{ }	…

### 1.2 数值类型

1.2.1 整数类型

数据类型	取值范围	转换函数	所占字节数
有符号8位整数	-2⁷~2⁷-1	int8	1
有符号16位整数	-2¹⁵~2¹⁵-1	int16	2
有符号32位整数	-2³¹~2³¹-1	int32	4
有符号64位整数	-2⁶³~2⁶³-1	int64	8
无符号8位整数	0~2⁸-1	uint8	1
无符号16位整数	0~2¹⁶-1	uint16	2
无符号32位整数	0~2³²-1	uint32	4
无符号64位整数	0~2⁶⁴-1	uint64	8

取整函数

函数	运算法则	示例
floor(x)	向下取整	floor(1.5)=1;floor(-2.5)=-3
ceil(x)	向上取整	ceil(1.2)=2;ceil(-2.5)=-2
round(x)	取最接近的整数（如果小数部分为0.5，则向绝对值大的方向取整）	round(1.5)=2;round(-2.5)=-3
fix(x)	向0取整	fix(1.2)=1;fix(-2.5)=-2

1.2.2 浮点数类型

数据类型	所占字节数	各位的用途	数值范围	转换函数
单精度	4	0_{22位表示小数部分<br>23}30位表述指数部分 31位表示符号（0正1负）	-3.4028e+38_{-1.1755e-38<br/>1.1755e-38}3.4028e+38	single
双精度	8	0_{51位表示小数部分<br/>52}62位表述指数部分 63位表示符号（0正1负）	-1.7977e+308_{-2.2251e-308<br/>2.2251e-308}1.7977e+308	double

1.2.3 复数类型

默认使用字母 i 或 j 作为虚部标志

>> x=3+4i
x =
   3.0000 + 4.0000i
   
>> x=5;
>> y=6;
>> z=complex(x,y);
z =
   5.0000 + 6.0000i

复数相关函数

函数	说明
real(z)	返回复数z的实部
imag(z)	返回复数z的虚部
abs(z)	返回复数z的模
angle(z)	返回复数z的幅角
conj(z)	返回复数z的共轭复数
complex(a,b)	以a为实部、b为虚部创建复数

1.2.4 inf 和 NaN

inf 无穷量

NaN（Not a number）

>> x=25/0
x =
   Inf
>> y=log(0)
y =
  -Inf

>> x=0/0
x =
   NaN
>> y=inf/inf
y =
   NaN

1.3 逻辑类型

非零数值–逻辑真（1）

数值零–逻辑假（0）

>> logical(10)
ans =
  logical
   1

>> logical(-1)
ans =
  logical
   1

>> logical(0)
ans =
  logical
   0

1.4 字符串

1.4.1 字符串基本操作

字符串构建

>> x='Your Name'
x =
    'Your Name'

>> y=char('your name')
y =
    'your name'

字符串查看

>> whos
  Name      Size            Bytes  Class    Attributes
  x         1x9                18  char               
  y         1x9                18  char

ASCII码查看

>> abs(x)
ans =
    89   111   117   114    32    78    97   109   101

>> abs(y)
ans =
   121   111   117   114    32   110    97   109   101

字符串访问

>> x='Your Name'
x =
    'Your Name'
    
>> z=x(6:9)
z =
    'Name'

字符串内加单引号

>> a='I''m right'
a =
    'I'm right'

1.4.2 字符串水平或垂直连接

>> x=['hello','kitty']
x =
    'hellokitty'

>> y=['hello';'kitty']
y =
  2×5 char 数组
    'hello'
    'kitty'
    
>>  strcat('hello','kitty')
ans =
    'hellokitty'

>> strvcat('hello','kitty')
ans =
  2×5 char 数组
    'hello'
    'kitty'

1.4.3 字符串其他命令

函数	功能
strcmp	比较字符串
strcmpi	忽略大小写比较字符串
strncmp	比较字符串的前n个字符
findstr	在一个字符串中查找另一个字符串
strjust	对其字符数组，包括左对齐、右对齐和居中
strmatch	查找匹配的字符串
strrep	替换字符串
upper	转换为大写
lower	转换为小写
strtok	返回字符串中的第一个分隔符（空格、回车和“Tab”键）前的部分
blanks	产生空字符串
deblank	删除字符串中的空格

1.5 结构体类型

后续补充

1.6 单元数组类型

后续补充

1.7 函数句柄

后续补充

二、基本矩阵操作

2.1 矩阵的创建

2.1.1 基本方法

>> A=[1,2,3;4,5,6;7,8,9]
A =
     1     2     3
     4     5     6
     7     8     9

>> B=[1 3 5;2 4 8]
B =
     1     3     5
     2     4     8

2.1.2 特殊矩阵

函数名	功能
zeros(m,n)	产生m*n的全0矩阵
ones(m,n)	产生m*n的全1矩阵
rand(m,n)	产生均匀分布的随机矩阵，元素取值范围0.0~1.0
randn(m,n)	产生正态分布的随机矩阵
magic(N)	产生N阶魔方矩阵（矩阵的行、列和对角线上的元素和相等）
eye(m,n)	产生m*n的单位矩阵

2.1.3 向量的创建

from:step:to from为开始值，to为结束值，step为步长（默认为1）

>> x=1:5
x =
     1     2     3     4     5

>> y=2:0.5:4
y =
    2.0000    2.5000    3.0000    3.5000    4.0000

>> z=[1:2:5;1:3:7]
z =
     1     3     5
     1     4     7

linspace(a,b,n) a为开始值，b为结束值，n为元素个数（线性分布，默认为100）
logspace(a,b,n) a为开始值，b为结束值，n为元素个数（对数分布，默认为50）

>> x1=linspace(0,2*pi,5)   %从0~2*pi等分成5个点
x1 =
         0    1.5708    3.1416    4.7124    6.2832

>> x2=logspace(0,2,3)      %从1~100对数等分成3个点
x2 =
     1    10   100

2.1.4 标量的创建

m=n=1，创建1*1矩阵，称为标量

>> x=2
x =
     2

>> y=[2]
y =
     2

>> size(x),size(y)
ans =
     1     1
ans =
     1     1

2.1.5 空矩阵的创建

m=n=0，或者m=0，或者n=0的矩阵，称为空矩阵

>> x=[]
x =
     []

>> size(x)
ans =
     0     0

>> whos x
  Name      Size            Bytes  Class     Attributes
  x         0x0                 0  double

2.2 矩阵大小的改变

2.2.1 矩阵合并

表达式C=[A B],表示水平方向合并矩阵A和B

表达式C=[A;B],表示竖直方向合并矩阵A和B

其他函数如表

函数名	函数描述	基本调用格式
cat	在指定方向合并矩阵	cat(DIM,A,B)在DIM维方向合并矩阵A、B cat(2,A,B) 与[A B]用途一致 cat(1,A,B) 与[A;B]用途一致
horzcat	在水平方向合并矩阵	horzcat(A,B) 与[A B]用途一致
vertcat	在垂直方向合并矩阵	vertcat(A,B) 与[A;B]用途一致
repmat	通过复制矩阵来构造新的矩阵	B=repmat(A,M,N) 得到M*N个A的大矩阵
blkdiag	用已知矩阵来构造对角化矩阵	Y=blkdiag(A,B,…) 得到以矩阵A,B,…为对角块的矩阵Y

2.2.2 矩阵行列的删除

对矩阵要删除的行或者列赋予一个空矩阵[]

>> A=magic(3)
A =
     8     1     6
     3     5     7
     4     9     2

>> A(:,3)=[]
A =
     8     1
     3     5
     4     9

2.3 矩阵下标引用

2.3.1 元素访问

一个m*n的矩阵A的第i行第j列的元素表示为A(i,j)

>> A=magic(3)
A =
     8     1     6
     3     5     7
     4     9     2

>> a=A(2,3)
a =
     7

>> A(3,3)=520
A =
     8     1     6
     3     5     7
     4     9   520

>> A(3,4)=111
A =
     8     1     6     0
     3     5     7     0
     4     9   520   111

提取矩阵元素值时，若元素下标(i,j)大于矩阵的大小(m,n)，则提示出错赋值矩阵元素值时，若元素下标(i,j)大于矩阵的大小(m,n)，则自动扩充矩阵，扩充部分以0填充

2.3.2 线性引用

matlab是按列优先排列的一个长列向量格式（线性引用元素）来储存矩阵元素的

>> A=magic(2)
A =
     1     3
     4     2

>> A(3)
ans =
     3

2.3.3 访问多个矩阵元素

操作符：可以用来表示矩阵的多个元素，用法简介如表

示例	功能
A(:😅	返回矩阵A的所有元素
A(i,:)	返回矩阵A第i行的所有元素
A(i,k1:k2)	返回矩阵A第i行的自k1~k2列的所有元素
A(:,j)	返回矩阵A第j列的所有元素
A(k1:k2,j)	返回矩阵A第j列的自k1~k2行的所有元素

>> A=magic(4)
A =
    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

>> B=A(3,:)
B =
     9     7     6    12

>> C=A(1:3,4)
C =
    13
     8
    12

2.4 矩阵信息获取

2.4.1 矩阵尺寸信息

函数名	函数描述	基本调用格式
length	矩阵最长方向的长度	n=length(X) 相当于max(size(X))
ndims	矩阵的维度	n=ndims(X)
numel	矩阵的元素个数	n=numel(X)
size	矩阵在各个方向的长度	d=size(X) 返回的大小信息以向量方式储存 [m,n]=size(X) 返回的大小信息以分开方式储存 m=size(X,dim) 返回某一位的大小信息

2.4.2 元素数据类型

函数名	函数描述	基本调用格式
class	返回输入数据的数据类型	C=class(obj)
classisa	判断输入数据是否为指定数据类型	K=isa(obj,‘class_name’)
iscell	判断输入数据是否为单元型	tf=ciscell(A)
iscellstr	判断输入数据是否为单元型的字符串	tf=iscellstr(A)
ischar	判断输入数据是否为字符数组	tf=ischar(A)
isfloat	判断输入数据是否为浮点数	tf=isfloat(A)
isinteger	判断输入数据是否为整数	tf=isinteger(A)
islogical	判断输入数据是否为逻辑型	tf=islogical(A)
isnumeric	判断输入数据是否为数值型	tf=isnumeric(A)
isreal	判断输入数据是否为实数	tf=isreal(A)
isstruct	判断输入数据是否为结构体	tf=isstruct(A)

2.4.3 矩阵数据结构

函数名	函数描述	基本调用格式
isempty	测试矩阵是否为空矩阵	tf=isempty(A)
isscalar	测试矩阵是否为标量	tf=isscalar(A)
issparse	测试矩阵是否为稀疏矩阵	tf=issparse(A)
isvector	测试矩阵是否为向量	tf=isvector(A)

2.5 矩阵结构的改变

函数名	函数描述	基本调用格式
reshape	按照列的顺序重新排列矩阵元素	B=reshape(A,m,n) 把矩阵变成m*n的大小
rot90	旋转矩阵90°	B=rot90(A) 旋转矩阵90° B=rot90(A,k) 旋转矩阵k*90°，k为整数
fliplr	以竖直方向为轴做镜像	B=fliplr(A)
flipud	以水平方向为轴做镜像	B=flipud(A)
flipdim	以指定的轴做镜像	B=flipdim(A，dim) 当dim=2时，以水平方向为轴做镜像当dim=1时，以竖直方向为轴做镜像
transpose	矩阵的转秩	B=transpose(A)
ctranpose	矩阵的共轭转秩	B=ctranpose(A)

三、运算符

3.1 算术运算符

数组运算		矩阵运算
命令	含义	命令	含义
A+B	对应元素相加	A+B	与数组运算相同
A-B	对应元素相减	A-B	与数组运算相同
S.*B	标量S分别与B元素的积	S*B	与数组运算相同
A.*B	数组对应元素相乘	A*B	内维相同矩阵的乘积
S./B	S分别被B的元素左除	S\B	B矩阵分别左除S
A./B	A的元素被B的对应元素除	A/B	矩阵A右除B（A的逆矩阵与B相乘）
B.\A	结果一定与上行相同	B\A	A左除B（invB乘以A）
A.^S	A的每个元素自乘S次	A^S	A矩阵为方阵时，自乘S次
A.^S	S为小数时，对A各元素分别裘非整数幂，得出矩阵	A^S	S为小数时，方阵A的非整数乘方
S.^B	分别以B的矩阵元素为指数求幂值	S^B	B为方阵时，标量S的矩阵乘方
A.’	非共轭转置	A’	共轭转置
exp(A)	以自然数e为底，分别以A的元素为指数求幂	expm(A)	A的矩阵指数函数
log(A)	对A的各元素求对数	logm(A)	A的矩阵对数函数
sqrt(A)	对A的各元素求平方根	sqrtm(A)	A的矩阵平方根函数

3.2 关系运算符

关系运算符	说明
<	小于
<=	小于等于
>	大于
>=	大于等于
==	等于
~=	不等于

针对两个相同长度的矩阵，指对两个矩阵的对应元素进行比较针对标量和矩阵，指标量与另一个矩阵的每个元素进行运算

>> magic(3)>3*ones(3)
ans =
  3×3 logical 数组
   1   0   1
   0   1   1
   1   1   0

3.3 逻辑运算符

a	b	a&b 与	a\|b 或	~a 非	xor(a,b) 异或
0	0	0	0	1	0
0	1	0	1	1	1
1	0	0	1	0	1
1	1	1	1	0	0

两个变量都是标量，则结果为0，1的标量两个变量都是数组，则必须大小相同，结果也是同样大小的数组一个数组和一个标量，则标量与数组的每个元素分别比较，结果为数组大小相同的数组

3.4 运算优先级

序号	运算符
1	圆括号（）
2	转置（.’），共轭转置(’)，乘方（.^{），矩阵乘方（}）
3	标量加法（+）、减法（-）、取反（~）
4	乘法（.），矩阵乘法（），右除（./），左除（.\），矩阵右除（/），矩阵左除（\）
5	加法（+），减法（-），逻辑非（~）
6	冒号运算符（:）
7	小于（<），小于等于（<=），大于（>），大于等于（>=），等于（==），不等于（~=）
8	数组逻辑与（&）
9	数组逻辑或（\|）
10	逻辑与（&&）
11	逻辑或（\|\|）

四、字符串运算函数与文件读取

后续补充

五、数值计算

5.1 矩阵基本运算

运算类型	运算符	描述	注意事项
加	+	对应元素相加	两个矩阵大小相同若有标量，则标量与矩阵的每个元素进行运算
减	-	对应元素相减	同上
乘	*	前矩阵各行元素与后矩阵各列元素对应相乘并相加	数组为“.*”
左除	\	A\B=inv(A)*B=x	A*x=B
右除	/	A/B=A*inv(B)=x	x*B=A
幂	^	A^B	A为标量或者矩阵方阵

5.2 矩阵其他运算

函数名	功能描述	基本调用格式
det(X)	计算方阵行列式	det(X)
rank(X)	求矩阵的秩，得出的行列式不为0的最大方阵边长	rank(a)
’	若矩阵A的元素为实数，则为矩阵转置若A为复数矩阵，则A转置后的元素由对应元素的共轭复数构成若仅希望转置，则使用：A.’	A’
inv(X)	求矩阵的逆矩阵方阵X的det(X)不为0，逆矩阵X^-1才存在，X*X^-1=0	inv(a)
[v,d]=eig(X)	计算矩阵特征值和特征向量如果Xv=vd存在非零解，则v为特征向量，d为特征值	[v,d]=eig(a)
diag(X)	产生X矩阵的对角阵	diag(v,k)
tril(X)	抽取X的主对角线的下三角部分构成矩阵	tril(X,k)
triu(X)	抽取X的主对角线的上三角部分构成矩阵	triu(X,k)

5.3 矩阵分解

后续补充完全

分解类型	函数名	函数描述	基本调用格式
Cholesky分解	chol	存在一个实的非奇异上三角矩阵R，满足R’*R=X	[R,p]=chol(X) Z正定时，p=0，反之p为正整数
LU分解	lu	将矩阵分解为下三角矩阵L和上三角矩阵U，满足LU=X	[L,U]=lu(X) [L,U,p]=lu(X) 此时LU=PX
QR分解
特征值分解
奇异值分解

5.4 线性方程组的求解

5.4.1 唯一解或特解

矩阵除法法：

A*X=B X=A\B

LU分解法（运算速度快）

A*X=B L* U *X=B X=U(L\B)

A =
     5     6     0     0     0
     1     5     6     0     0
     0     1     5     6     0
     0     0     1     5     6
     0     0     0     1     5
B =
     1
     0
     0
     0
     1
     
%矩阵除法
>> C=rank(A)
C =
     5

>> X=A\B
X =
    2.2662
   -1.7218
    1.0571
   -0.5940
    0.3188
  
%LU分解法
>> D=det(A)
D =
   665

>> [L U]=lu(A)
L =
    1.0000         0         0         0         0
    0.2000    1.0000         0         0         0
         0    0.2632    1.0000         0         0
         0         0    0.2923    1.0000         0
         0         0         0    0.3081    1.0000

U =
    5.0000    6.0000         0         0         0
         0    3.8000    6.0000         0         0
         0         0    3.4211    6.0000         0
         0         0         0    3.2462    6.0000
         0         0         0         0    3.1517

>> X=U\(L\B)
X =
    2.2662
   -1.7218
    1.0571
   -0.5940
    0.3188

5.4.2 齐次方程组的通解

线性齐次方程组

非线性齐次方程组

后续补充

5.5 多项式

5.5.1 多项式求值

语法：ployval(p,s)

p为多项式，s为给定矩阵

>> %求多项式P1=5x^3-3x^2+2当x=[0 2 -1 3]时的值
>> p1=[5 -3 0 2]
p1 =
     5    -3     0     2

>> s=[0 2 -1 3]
s=
     0     2    -1     3
     
 polyval(p1,s)
ans =
     2    30    -6   110

5.5.2 多项式的根

语法：r=roots(p)

p为多项式，r为多项式的根，以列向量的方式保存

语法：p=poly(r)

根据多项式的根来计算多项式的系数

>> %计算多项式 P=x^3+15x^2-8x+10 的根以及反算系数
>> p=[1 15 -8 10]
p =
     1    15    -8    10

>> r=roots(p)
r =
 -15.5556 + 0.0000i
   0.2778 + 0.7521i
   0.2778 - 0.7521i

>> p=poly(r)
p =
    1.0000   15.0000   -8.0000   10.0000

5.5.3 多项式的运算

>> p1=[1 0],p2=[1,1],p3=[1,20]
p1 =
     1     0
p2 =
     1     1
p3 =
     1    20
     
>>  P=p1+p2,Q=p2-p3 %加法、减法
P =
     2     1
Q =
     0   -19
     
>> X=conv(p1,p2) %乘法
X =
     1     1     0
>> X=conv(X,p3)
X =
     1    21    20     0
     
>> [q,r]=deconv(X,p3) %除法，q为商，r为余子式
q =
     1     1     0
r =
     0     0     0     0
     
>> p=polyder(X) %求导
p =
     3    42    20
>> p=polyder(p1,p2) %p1，p2乘积的求导
p =
     2     1
     
>> [p,q]=polyder(p1,p2) %p1，p2之商的求导，p为分子，q为分母
p =
     1
q =
     1     2     1

5.6 数据插值

后续补充

5.7 曲线拟合

后续补充

5.8 函数极限、微分、积分

5.8.1 函数极限

limit(s,n,inf)返回符号表达式当n趋于无穷大时表达式s的极限

limit(s,x,a)返回符号表达式当x趋于a时表达式s的极限

limit(s,x,a,left)返回符号表达式当x趋于a-0时表达式s的左极限

limit(s,x,a,right)返回符号表达式当x趋于a-0时表达式s的右极限

>> syms n
 
>> y=10*(1+0.05/n)^n
 y =
 10*(1/(20*n) + 1)^n
 
>> limit(y,n,inf)
 ans =
10*exp(1/20)

5.8.2 函数微分

diff(s,x,n)返回符号表达式s对自变量x的n阶导数

>> syms a b c x
>>  f=a*x^2+b*x+c
 f =
a*x^2 + b*x + c
 
>> diff(f)
 ans =
 b + 2*a*x
 
>> diff(f,a)
 ans =
x^2
 
>> diff(f,x,2)
ans =
 2*a
 
>> diff(f,3)
 ans =
 0

5.8.3 函数积分

[I,n]=quad('filename',a,b,tol,trace)

filename为被积函数； a和b控制下限和上限； tol控制积分精度（缺省0.001）； trace控制积分过程的展现，非0展现，0不展现（缺省为0）；返回参数I为定积分值，n为被积函数的调用次数。

[I,n]=quadl('filename',a,b,tol,trace)

tol缺省为10-6，其余同上

如果不建立被积函数的函数文件，则需使用语句函数（内联函数）eg.fx=inline('x+1')

I=quadl('filename',a,b,c,d,tol,trace)

计算函数在[a,b]X[c,d]区域的二重定积分，其余同上

六、符号计算

6.1 符号对象及表达式的创建

命令	含义
x=sym(‘a’)	建立符号常量
syms x y z	建立符号变量

>> m=sym('m')
 m =
 m
 
>> syms x a b c d

>> f=sin(x)^2 %赋给变量f符号表达式
 f =
 sin(x)^2
 
>> eq='a*x^2+b*x+c=0' %赋给变量eq符号方程
eq =
    'a*x^2+b*x+c=0'

>>  syms d %创建符号矩阵
>> A=[a b;c d]
A =
[ a, b]
[ c, d]

6.2 符号对象基本运算

基本运算：基本相同于数值计算
关系运算：没有“大于、大于等于、小于、小于等于”；==和~=为相等和不等的比较
函数运算：基本相同于数值计算
符号与数值对象的转换 X=vpa(S,n) N=double(S)

>> a1=sym(2*pi)
a1 =
 2*pi
 
>> b1=double(a1)
b1 =
    6.2832

>> b2=vpa(a1,32)
b2 =
6.283185307179586476925286766559

6.3 符号表达式的替换

语句：subs(S,old,new)，用新变量new替换S中指定的变量old

>> syms a b c
>> c=a+b
c =
 a + b
 
>> a=2
a =
     2

>> c
 c =
a + b
 
>> subs(c)
 ans =
 b + 2

>> subs(c,b,3)
 ans =
 a + 3

6.3 精度计算

语句：digits(n) 设定默认的精度

语句：S=vpa(s,n) 将s表示为n位有效位数的符号对象

语句：format 修改显示的有效位数（数值）

6.4 符号表达式的化简

函数名	函数描述
pretty	将给出排版形式的输出结果
collect	将表达式中相同次幂的项合并，或指定哪个变量的幂次合并
expand	将表达式展开成多项式形式
horner	将表达式转换为嵌套形式
factor	将表达式转换为因式形式
simplify	利用函数规则对表达式进行化简
simple	调用matlab其他函数对表达式进行综合化简，并显示化简过程

>> f=x^3-6*x^2+11*x-6     %多项式形式
 f =
 x^3 - 6*x^2 + 11*x - 6
 
>> g=(x-1)*(x-2)*(x-3)    %因式形式
 g =
 (x - 1)*(x - 2)*(x - 3)
 
>> h=x*(x*(x-6)+11)-6     %嵌套形式
 h =
 x*(x*(x - 6) + 11) - 6
 
>> pretty(f)              %排版输出
 3      2
x  - 6 x  + 11 x - 6

>> collect(g)             %合并同类项
 ans =
 x^3 - 6*x^2 + 11*x - 6
 
>> expand(g)              %展开为多项式
 ans =
 x^3 - 6*x^2 + 11*x - 6
 
>> horner(f)              %转换为嵌套
 ans =
 x*(x*(x - 6) + 11) - 6
 
>> factor(f)              %转换为因式
 ans =
 [ x - 3, x - 1, x - 2]
 
>> y=cos(x)^2+sin(x)^2
 y =
 cos(x)^2 + sin(x)^2
 
>> simplify(y)            %化简函数
 ans =
 1

6.5 符号微分、积分

6.5.1 符号微分

diff(f,a,n)

a为指定变量，默认为x

n为n次微分，默认为1

>> syms x b t
>> f = x^3 + 2*x^2 - b*x + 5
f =
 x^3 + 2*x^2 - b*x + 5
 
>> diff(f)
ans =
3*x^2 + 4*x - b
 
>> diff(f,b)
ans =
 -x
 
>> diff(f,3)
 ans =
 6
 
 >> A = [sin(x)  t^2; x + 2  6*b]
 A =
[ sin(x), t^2]
[  x + 2, 6*b]
 
>> diff(A)
ans =
[ cos(x), 0]
[      1, 0]

6.5.2 符号表达式级数

symsum(s,x,a,b) 级数和

taylor(F,x,n) 泰勒展开

后续补充

6.5.3 符号积分

int(f,t,a,b)

符号表达式对变量t（默认x）的积分，积分区间为[a,b]

>> syms x y 
>> f=x^3+8
f =
 x^3 + 8
 
>> int(f,2,3)
ans =
97/4

>> g=x*exp(-x*y)
g =
x*exp(-x*y)

>> int(int(g,x),y) 
ans =
exp(-x*y)/y

6.5.4 符号积分变换

F=fourier(f,t,w) 傅里叶变换

f=ifourier(F,w,t) 傅里叶反变换

F=laplace(f,t,s) 拉普拉斯变换

f=ilaplace(F,s,t) 拉普拉斯反变换

F=ztrans(f,n,z) Z变换

f=iztrans(F,z,n) Z反变换

后续补充

6.6 符号方程求解

代数方程求解

solve(eq,v)

求方程关于指定变量的解

>> syms a b c x y z

>>  f1=a*x^2+b*x+c
f1 = 
a*x^2 + b*x + c
 
>> solve(f1) 
ans =
 -(b + (b^2 - 4*a*c)^(1/2))/(2*a)
 -(b - (b^2 - 4*a*c)^(1/2))/(2*a)
 
 eq1=x^2+2*x+1
 eq2=x+3*z-4
 eq3=y*z+1
 >> [x,y,z]=solve(eq1,eq2,eq3)
 x =
 -1
y =
-3/5
z = 
5/3

微分方程求解

dsolve(eq,con,v)

eq为微分方程，con微分初始条件，v自由变量

y的一阶导数dy/dx或者dy/dt表示为Dy

y的n阶导数dⁿy/dⁿx或者dⁿy/dⁿt表示为Dny

>> syms x y

>> dsolve('x*D2y-3*Dy=x^2',x)
ans =
C4*x^4 - x^3/3 + C3

>> dsolve('x*D2y-3*Dy=x^2','y(1)=0','y(5)=0',x)
ans = 
(31*x^4)/468 - x^3/3 + 125/468

>> [x,y]=dsolve('Dx=y,Dy=-x') 
x =
C8*cos(t) + C7*sin(t)
y = 
C7*cos(t) - C8*sin(t)

七、Malab计算可视化

7.1 二维图形

7.1.1 基本命令

plot(x,y,'s')

x=-2*pi:pi/100:2*pi;
y1=x+1;
y2=sin(x);
y3=cos(x);
plot(x,y1,x,y2,x,y3)

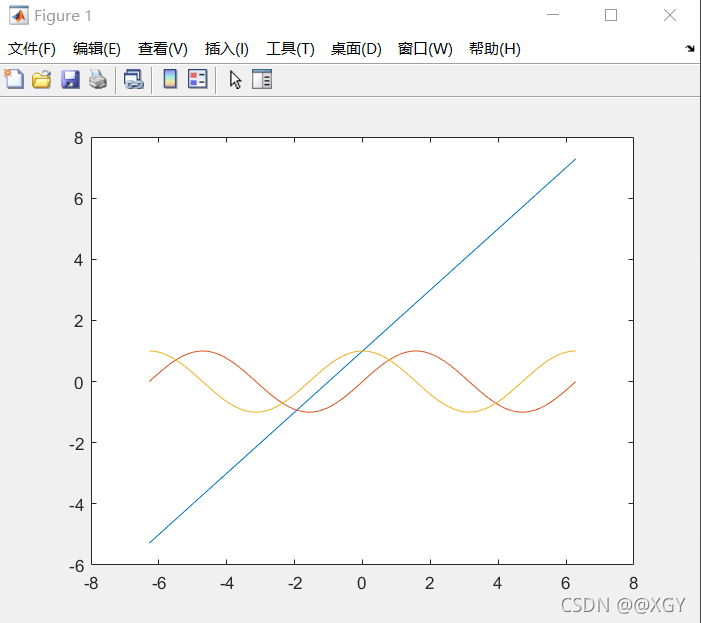
在这里插入图片描述

7.1.2 线型、颜色和数据点型

polt(x.y.'string')

线型		颜色		数据点型
类型	符号	类型	符号	类型	符号
黄色	y	实线	-	实点标记	.
紫色	m	点线	：	圆圈标记	o
青色	c	点划线	-.	叉号形	x
红色	r	虚线	–	十字形	+
绿色	g			星号标记	*
蓝色	b			方块标记	s
白色	w			钻石形标记	d
黑色	k			向下三角标记
				向上三角标记
				向左三角标记	<
				向右三角标记	>
				五角星标记	p
				六连形标记	h

7.1.3 标注、说明和网格

文字标注

语法	含义
title(‘string’)	书写图名
xlabel(‘string’)	横坐标轴名
ylabel(‘string’)	纵坐标轴名
lengend(_,‘Location’,lcn)	在指定位置建立图例
lengend off	擦除当前图中图例
text(xt,yt,‘string’)	在图形的（xt,yt）坐标处书写文字注释
gtext(‘string’)	在图形中手动添加文字注释
grid on	显示分格线
grid off	不显示分格线
grid	以上命令切换

7.1.4 叠图、子图

语法	含义
subplot(m,n,k)	使m*n幅子图中的第k幅成为当前图
hold on	启动图形保持功能
hold off	关闭图形保持功能
hold	以上命令切换

x=-2*pi:pi/20:2*pi;
y1=x+1;
y2=sin(x);
y3=cos(x);
y4=x.^2;
subplot(1,2,1)
plot(x,y1,'r-+',x,y4,'y-')
grid on 
title('XGY练习图像1');
xlabel('x1');
ylabel('y1');
legend('x+1','x.^2');
text(-4,-4,'x+1')
subplot(1,2,2)
plot(x,y2,'g--')
hold on
plot(x,y3,'k*')
title('XGY练习图像2');
xlabel('x2');
ylabel('y2');
legend('sin(x)','cos(x)');
text(0,-0.4,'sin(x)')
gtext('cos(x）')

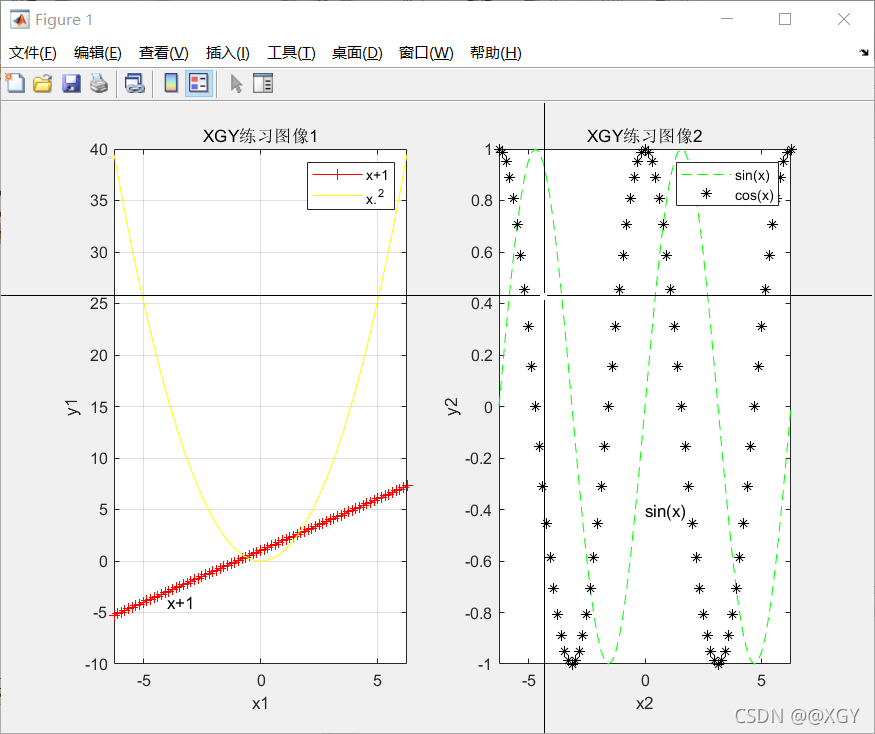
在这里插入图片描述

7.1.5 坐标轴控制

命令	含义	命令	含义
axis auto	使用默认设置	axis equal	纵横坐标采用等长刻度
axis manual	使当前坐标范围不变	axis fill	在manual方式下起作用，使坐标充满整个绘图区
axis off	取消轴背景	axis image	纵横坐标采用等长刻度，且坐标框紧贴数据范围
axis on	使用轴背景	axis normal	默认矩形坐标系
axis jj	矩阵式坐标，原点在左上方	axis square	产生正方形坐标系
axis xy	普通直角坐标，原点在左下方	axis tight	把数据范围直接设为坐标范围
axis([xmin,xmax,ymin,ymax])	设定坐标范围	axis vis3d	保持高宽比不变，用于三维旋转时避免图形大小变化
box on	使当前坐标框封闭	box off	使当前坐标框开启

7.2 三维图形

7.2.1 基本命令

plot3(x,y,z,'s')

t=[0:0.1:10*pi];
x=2*t;
y=sin(t);
z=cos(t);
plot3(x,y,z,'r*')

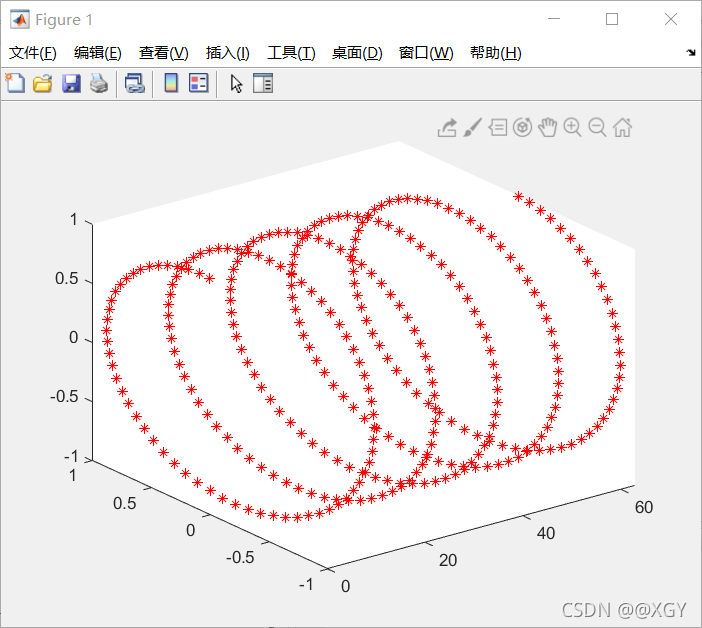
在这里插入图片描述

7.2.2 三维网线图、表面图

后续补充

7.2.3 立体图形与图轴控制

后续补充

7.3 特殊图形

函数	图形
bar	条形图
pie	饼形图
hist	统计直方图
polar	极坐标图
stairs	阶梯图
stem	火柴杆图
scatter	离散点图
area	面积图
fill	填充图
compass	射线图
feather	羽毛图
contour	等高线图

八、程序设计

8.1 函数

结构：function [outputArg1，outputArg2]=filename(inputArg1，inputArg2)

调用：[输出实参表]=函数名(输入实参表)

补充函数： nargin：在函数体内获得确定输入变量的个数 nargout：在函数体内获得确定输出变量的个数 vnargin：作为输入参数，个数可变 vnargout：作为输出参数，个数可变 ploy2sym：系数组变换为符号多项式 sym2ploy：符号多项式变换为系数组

function f=ex603(a,b,c)
if nargin==0
    a=0;b=0;c=0;
elseif nargin==1
        b=0;c=0;
elseif nargin==2
            c=0;
end
        f=a+b+c;
end

>> f=ex603(5)
f =
     5

>> f=ex603(2,6)
f =
     8

>> f=ex603(5,2,1)
f =
     8

>> f=ex603(1,2,3,4)
错误使用 ex603
输入参数太多。

8.2 脚本

类似于命令窗口

驻留工作空间

命令窗口键入脚本名即可运行

8.3 变量

全局变量：

定义：global 变量名

删除：clear global a 清除某个全局变量 / clear global 清除所有全局变量

永久变量

定义：persistent 变量名

8.4 程序控制结构

8.4.1 顺序结构

数据输入 input

A=input(提示信息，选项)

数据输出 disp

disp(输出项)

clear
a=input('赋值a=');
b=input('赋值b=');
c=a+b;
disp(c)

>> xgy2
赋值a=5
赋值b=6
    11

8.4.2 循环结构

for…while循环

for （循环变量=开始值：增量：结束量） %步长为1时，增量忽略 end

for (i=1:3)
    for (j=1:4)
        A(i,j)=2;
    end
end
disp(A)

>> xgyfor
     2     2     2     2
     2     2     2     2
     2     2     2     2

while…end循环

while 表达式 %表达式为逻辑真时，执行循环体语句循环体语句 end

clear
n=0;
sum=0;
while n<=100
      sum=sum+n;
      n=n+1
end
sum
n

sum =
   5050
n =
   101

8.4.3 选择结构

if结构

if 条件语句组1 else 语句组2 end

if 条件1 语句组1 elseif 条件2 语句组2 elseif 条件3 语句组3 else 语句组4 end

clear
a=input('请输入a=');
b=input('请输入b=');
if a>b
    disp('最大值=')
    disp(a)
elseif a<b
    disp('最大值=')
    disp(b)
elseif a==b
    disp('相等')
end

请输入a=5
请输入b=6
最大值=
     6

>> xgyif
请输入a=4
请输入b=4
相等

switch…case结构

switch 表达式 %必须是标量或者字符串 case 值1 语句组1 case 值2 语句组2 otherwise 语句组3 end

clear
score=input('请输入您的分数')
switch floor(score/10)
    case{10,9}
        grade='优';
    case{8}
        grade='良';
    case{7}
        grade='中';
    case{6}
        grade='及格';
    otherwise
        grade='不及格';
end
disp(grade)

请输入您的分数56
score =
    56
不及格

请输入您的分数89
score =
    89
良

8.4.3 其他控制语句

break命令

强制终止for循环、while循环，执行end后面的命令，通常与if语句结合使用（跳出）

continue命令

结束本次for循环、while循环，但是继续执行下一循环（跳过）

return命令

终止当前命令的执行或被调用函数的运行，立即返回上一级或等待输入命令

pause命令

控制程序运行暂停，按任意键继续，可调整暂停时间

8.5 程序调试

8.5.1 直接调试

查看变量值：将函数中要调试的语句后面的分号（；）删除，将结果显示在命令窗口中，通过显示的结果进行查找，同时可以利用disp函数显示中间变量的值。
改写函数文件：调试一个单独函数时，可以通过注释声明语句等方式将函数改写为脚本文件，这样可以直接对输入参数赋值，然后以脚本方式运行M文件，保存变量至工作空间，以便查看和调试
添加keyboard指令：使得matlab执行到此处时暂停，并在命令窗口显示k>>提示符，用户可以查看工作空间中的变量，可以改变变量的值，输入return指令返回程序，继续执行。
利用echo命令：echo on用于显示脚本文件执行的过程；如果希望检查函数文件的内容，则使用echo 文件名 on命令；echo off用于关闭脚本文件的执行过程，echo 文件名 on用于关闭函数文件执行过程的显示

8.5.2 工具调试

设置断点时程序调试的重要手段之一，当程序运行到断点处时会暂停，此时可以通过检查相关变量的值等方式来确定程序运行的正确性。
在这里插入图片描述

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删

返回上级列表

请

联系我们

，获取更多内容

< 上一篇: Matlab控制应用：自动小车仿真实例

下一篇: Matlab绘图技巧：绘制圆形的方法 >

Matlab基础操作入门教程

Matlab

一、matlab使用基础

1.1 通用命令

1.1.1 通用命令

1.1.2 输入内容的编辑

1.1.3 标点

1.2.1 整数类型

1.2.2 浮点数类型

1.2.3 复数类型

1.2.4 inf 和 NaN

1.3 逻辑类型

1.4 字符串

1.4.1 字符串基本操作

1.4.2 字符串水平或垂直连接

1.4.3 字符串其他命令

1.5 结构体类型

1.6 单元数组类型

1.7 函数句柄

二、 基本矩阵操作

2.1 矩阵的创建

2.1.1 基本方法

2.1.2 特殊矩阵

2.1.3 向量的创建

2.1.4 标量的创建

2.1.5 空矩阵的创建

2.2 矩阵大小的改变

2.2.1 矩阵合并

2.2.2 矩阵行列的删除

2.3 矩阵下标引用

2.3.1 元素访问

2.3.2 线性引用

2.3.3 访问多个矩阵元素

2.4 矩阵信息获取

2.4.1 矩阵尺寸信息

2.4.2 元素数据类型

2.4.3 矩阵数据结构

2.5 矩阵结构的改变

三、运算符

3.1 算术运算符

3.2 关系运算符

3.3 逻辑运算符

3.4 运算优先级

四、字符串运算函数与文件读取

五、数值计算

5.1 矩阵基本运算

5.2 矩阵其他运算

5.3 矩阵分解

5.4 线性方程组的求解

5.4.1 唯一解或特解

5.4.2 齐次方程组的通解

5.5 多项式

5.5.1 多项式求值

5.5.2 多项式的根

5.5.3 多项式的运算

5.6 数据插值

5.7 曲线拟合

5.8 函数极限、微分、积分

5.8.1 函数极限

5.8.2 函数微分

5.8.3 函数积分

六、符号计算

6.1 符号对象及表达式的创建

6.2 符号对象基本运算

6.3 符号表达式的替换

6.3 精度计算

6.4 符号表达式的化简

6.5 符号微分、积分

6.5.1 符号微分

6.5.2 符号表达式级数

6.5.3 符号积分

6.5.4 符号积分变换

6.6 符号方程求解

七、Malab计算可视化

7.1 二维图形

7.1.1 基本命令

7.1.2 线型、颜色和数据点型

7.1.3 标注、说明和网格

7.1.4 叠图、子图

7.1.5 坐标轴控制

二、基本矩阵操作