图像配准 是将在同一场景下,但不同时间点,或不同视角,或不同采集设备拍摄的多幅(≥2)图像进行匹配。假设有两幅图像 Fixed Image 和 Moving Image,图像配准就是要寻找一种空间变换(Transformation),将 moving image 变换到 fixed image 上,使得两幅图中对应同一空间位置的点一一对应,从而达到信息融合的目的。图像配准英文通常为:Image Registration,还有一些别名包括:Image Fusion,Superimposition,Matching,Merge。
注:上面说了图像配准是将 moving image(B)通过变换配准到 fixed image(A)上。实际上,要首先将 A 和 B 中的点都换算到世界坐标系中,即先计算 A-to-world 转换坐标 M A M_A MA,再计算 world-to-B 转换坐标 M B − 1 M_B^{-1} MB−1,最终将 B 配准到 A 的转换是 M B − 1 M A M_B^{-1}M_A MB−1MA。在配准应用时,换算到世界坐标系的过程被我们省略了。
【图像配准目标】 在几何上对齐两个图像,即让两幅图像在空间坐标上一致。
【图像配准需求来源】 刚开始看图像配准,我在想为什么要这么做,把两幅图统一起来有什么意义?
由于不同的成像条件(时间、视角、相机),导致对同一对象的成像结果有差异。而许多图像分析任务,比如图像融合、变化检测都需要将多幅图像统一到一个坐标系下,因此图像配准就是它们的关键前置任务。
以医学图像应用举例:医学图像配准需求的来源,就是医学图像有多种模态的数据(比如 CT,MR,超声,PET,SPECT),不同模态的图像能够反映人体的不同特征,比如 MRI 反应人体解剖结构,PET 反应人体功能结构。那么医生就希望这些图像能够叠加在一个坐标系下(同一基准下)反应人体结构特点,而不需要靠自己的想象来实现图像叠加。
(上图是将一个人大脑的核磁共振图像(左)与其大脑的功能图像(中)进行配准,得到叠加结果(右)以同时展示解剖结构信息和功能信息)
由于待配准的图像具有多样性,因此无法设计出一种通用的配准方法用于所有任务。在设计配准方法时,要从数据角度和应用角度出发,综合考虑图像的特征、假定的几何变形类型、图像噪声、所需的配准精度等信息。
【说明-1】临床诊断: 将同一病人的多模态术前图像进行叠加,帮助医生更精确地观察病灶和解剖结构。
(上图 Moving image 为 DTI 图像,能够展示人体大脑内神经束的走向;Fixed image 为 MR 图像,通过核磁共振展示病人大脑内的肿瘤,此时需要将病人大脑肿瘤切除,同时不能伤害神经结构,就需要将两幅图像叠加起来)
【说明-2】患者与标准图谱: 临床上有大量的解剖图谱,是根据前人经验绘制的标准人体解剖结构。利用计算机可以将这些标准图谱扫描到计算机中对病人的解剖结构进行分割。但是每一个具体的病人,其解剖结构不一定是标准结构,可能会有差别,所以就需要将标准图谱与具体病人的影像进行叠加,帮助理解具体病人的解剖结构。
图像配准的分类标准不唯一,常见的包括:
【说明-3】按图像采集方法分类:
【说明-4】按配准思想分类:
基于图像本身的配准方法(Image-based)包括:
【说明-5】按变形类型分类:
图像的空间变换可以分为刚体变换(Rigid)和非刚体变换(Deformable),其中:
注意:线性配准(Linear Registration)不是刚体配准(Rigid Registarion),刚体配准只是线性配准中的一部分。线性配准包括三个基本操作:平移(Translation),放缩(Scaling),旋转(Rotation),也允许一些其他变换操作,比如对边的平行移动,将一个正方形变成平行四边形,但线性配准不允许局部形变。
医学图像通用配准框架: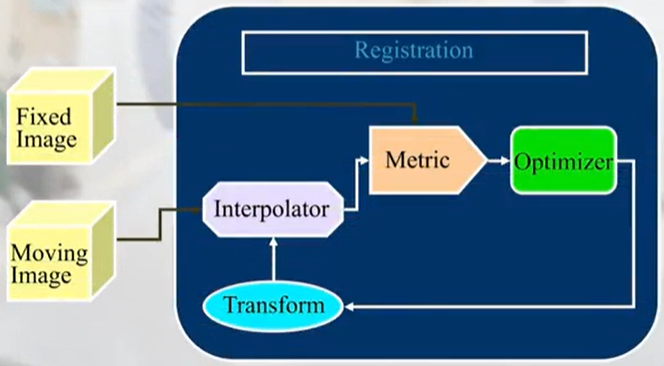
moving image 将参照 fixed image 进行形变,在形变过程中可能会丢失像素,因此需要 Interpolator,即插值。可以用不同的插值方法对缺失的像素点进行恢复。接着,测量变换后的 moving image 和 fixed image 间相似性的标准叫 Metric,标准也有很多方法实现。对转化矩阵 Transform 进行形变,通过迭代更新 Optimizer 达到最优。
通常,配准过程包含四个步骤:特征检测(Feature detection),特征匹配(Feature matching),变换模型估计(Transform model estimation)和 图像重采样和变换(Image resampling and transformation)。
传统的特征检测过程,特征是由专家手动进行选择。在自动特征检测方面,主要有两种方法:基于区域的方法(Area-based methods)和 基于特征的方法(Feature-based methods)。基于区域的方法不进行显著特征检测,直接将预定义大小的窗口甚至是整幅图像作为特征用于特征匹配步骤,所以严格来说称不上是特征检测。基于特征的方法提取图像中的显著特征,比如重要区域(森林、湖泊、田野),线(区域边界、海岸线、道路、河流),点(区域拐点,线段交叉点,高曲率曲线上的点)等。与基于区域的方法相比,基于特征的方法不直接处理图像强度值,而是使用了更高级的特征信息。这样做有利于适应光照改变或多采集设备分析的情况。
显著特征需要有一下几个特性:
基于特征的方法需要提取包括:区域特征(Region features),线特征(Line features),点特征(Point features)
总结:对于特征比较明显的图像(比如遥感和计算机视觉应用),推荐使用基于特征的特征检测方法,因为这些图像包含很多可识别的细节(城镇、河流、道路、森林、房间设施等)。但医学图像通常没有丰富的细节信息,通常会采用基于区域的特征检测方法。医学图像应用中,还可以通过专家交互式地选择或引入患者的外在特征,来补充显著特征的缺失 [123]。
关于基于区域和基于特征的特征检测方法实用性 survey:[151],分析了对于各种对比度和清晰度图像的适用性。此外,现在已经有了同时使用基于区域和基于特征的特征检测方法[85]。
从 moving image 和 fixed image 中分别完成特征检测后,检测到的特征可以通过两图像相近区域的平均图像强度、特征空间分布或特征描述符来进行匹配。另外有些工作将特征检测和特征匹配两步进行了融合,即在检测两幅图的对应特征时,也同时估计映射函数(mapping function)的参数。
Area-based methods:基于区域的方法也叫 correlation-like methods 或者 template matching。在 4.1 已经提到过,这类方法严格上说没有特征检测步骤,也就是不对图像中的显著特征进行检测,而直接将预定义大小的窗口,甚至是整幅图像用于特征匹配步骤【4,12,145】。
基于区域的方法局限性在于:1)简单地使用窗口只能对刚性变换(例如平移、旋转等)进行配准,如果图像间发生了更复杂的弹性变换(例如透视变换等),那么简单的窗口就无法进行配准,这也是基于区域方法基本思想的固有缺点;2)对于 moving image 和 fixed image 中不具有 “显著性” 的窗口内容,可能会导致无法正确匹配;3)特征的检测应当是在图像的不同部分进行选取,而基于窗口的选择方法也无法做到这一点。
基于相关性的方法(Correlation-like methods):基本思想是度量 moving image 和 fixed image 之间的相似度,目标是找出相似度最大的窗口对,通过不断匹配窗口对达到匹配两幅图像的目的。
(1)经典的基于区域的特征匹配方法:Cross-Correlation(CC),通过图像的强度直接对图像进行匹配,而不使用任何图像结构上的分析。因此CC的缺点:对图像的强度变化很敏感。通常,图像噪声、拍摄时照明强度的变化、使用不同的采集设备都会导致图像强度发生变化。CC的基本思想:计算 moving image 和 fixed image 中窗口对(window pairs)之间的相似性,并搜索相似性最大的两个窗口对(最大化问题),搜索的最优结果就是匹配的窗口对。根据 CC 方法的基本思想可以知道,它比较适用于匹配空间位置发生平移的图像,但其实它对轻微的旋转和缩放也能够适用。CC计算相似性:
基于 CC,还有 Normalized CC 和很多变体方法【146】。为了使 CC 能够处理平移之外的其他复杂几何变形,【17,83】提出为每个假定的几何变换都计算一次 CC,【170】解决因透视变化和因镜头缺陷而导致不同的配准问题,【98,99】解决图像存在部分遮挡的配准问题。
(2)与 CC 类似的方法是 Sequential Similarity Detection Algorithm(SSDA),使用顺序搜索策略和 L1 距离作为距离度量标准。SSDA的基本思想:计算窗口对间图像强度值差的绝对值(L1 距离)并求和,若累加和超过了给定的阈值,则说明该窗口对不匹配。SSDA 相比 CC,计算方法更简单,因此速度更快,但是可能不如 CC 准确。在距离度量的方法上,还可以使用平方差之和(Sum of squared differences)【211】。
(3)第三种方法是 Correlation Ratio-based Method(CR),与 CC 不同的是,CR 假设图像强度可以由函数进行表示,因此 CR 能够处理图像间强度不一致(多模态图像)的问题。关于多模态图像匹配的各种方法比较,可以参考【154】。
Correlation-like methods 的两个主要缺点:
傅里叶方法(Fourier methods)适合以下几种情况的特征匹配:
(细节没看,回头再补上吧)
基于互信息(Mutual Information,MI)的方法:MI 来源于信息论,用于衡量两个数据集之间统计概念上的依赖性,尤其适用于不同模态的图像配准。比如在医学图像配准应用中,需要将患者的解剖图像和功能图像进行配准以辅助诊断。MI方法的基本思想:通过最大化 MI,找到最优解。
两个随机变量 X 和 Y 之间的 MI 由下式给出,其中 H ( X ) = − E X ( l o g ( P ( X ) ) ) H(X) = -E_X(log(P(X))) H(X)=−EX(log(P(X))) 表示随机变量 X X X 的熵, P ( X ) P(X) P(X) 表示 X X X 的概率分布。
基于优化的方法:要求取最小差异度量或最大相似度量是一个多维优化问题,其维度就是几何变换的自由度。问题的自由度越高或相似性度量越复杂,就需要越复杂的优化算法来寻找全局最大值。优化方法的基本思想:将匹配问题看作一个寻找全局最大/最小值的优化问题,设计能量函数(Energy function)并将其最小化,当能量函数达到最小时就找到了最优解。另外,能量函数通常由两部分组成,一项是相似性度量/相异性度量,另一项是正则化项/惩罚项。在刚体变换问题中,正则化项通常被省略,但在非刚体变换中,通常存在正则化项。
关于优化方法的论文,可以参考:
【166】使用 Gauss-Newton 数值最小化算法对平方差之和进行最小化;
【201】使用 Gradient descent 优化算法寻找 MI 的最大值;
【164】使用 Levenberg-Marquardt 优化算法最小化对应像素间的强度差异。
在第一步特征检测之后,我们能够得到由控制点(CPs)表示的图像特征,例如点特征(点本身),线特征(线端点或线中点),区域特征(区域重心),基于特征的匹配方法目的是使用这些特征的空间关系或各种特征描述符找到它们之间的成对对应关系。
基于特征空间关系的方法:基本思想是利用控制点之间的距离和它们的空间分布完成特征匹配。通常适用于检测到的特征比较模糊,或特征邻域局部失真的情况。
关于基于特征空间关系的论文,可以参考:
【71】利用 Graph matching algorithm(图匹配算法)进行配准;
【175】利用 Clustering techinique(聚类技术)进行配准;
【14,22】利用 chamfer matching 进行配准;
【18】Iterative Closest Point(ICP) 算法用于 3D 图像配准。
基于特征描述符:基本思想是利用特征的描述符来估计特征间的对应关系,即匹配 moving image 和 fixed image 中具有最相似描述的特征。在特征描述空间中寻找最佳匹配特征对时,可以使用带阈值的最小距离规则或匹配似然系数。
特征描述符需要满足以下几个条件,但这些条件不一定都必须(能够)满足:
[todo]
[todo]
当待配准的图像没有很多细节信息,且显著特征是由图像灰度而非局部形状或结构提供时,优先考虑使用基于区域的特征匹配方法。为了加快搜索速度,基于区域的方法通常采用金字塔图像表示和复杂的优化算法来找到相似矩阵的最大值。基于区域的匹配方法缺点在于:1)moving image 和 fixed image 必须具有相似的强度函数,也就是强度函数要么相同,要么至少是具有统计意义上的相关性(常见于多模态图像配准);2)只允许图像间的平移或小幅度的旋转,尽管现在基于区域的方法也可以推广到完全旋转和缩放,但由于计算量太大实际应用中不常用。
当图像的局部结构信息更重要时,则优先使用基于特征的匹配方法,其能够配准不同性质的图像,可以处理复杂的图像失真问题。使用基于特征的方法关键是要有鲁棒的特征描述符,即对图像间所有假定的差异都具有不变性。基于特征的匹配方法共有缺点在于,特征可能难以检测,或存在时间上的不稳定因素。
什么是 Transformation?Transformation 关系到两幅图特征位置的变换(坐标转换),主要包括以下四种变换方式:

配准算法(Registration algorithms)的目的就是找到变换模型(Tranformation),即找到坐标转换矩阵,以实现两个不同图像的融合。配准算法可以分为 Rigid & Affine 类算法,Non-rigid 类算法,
1. Rigid & Affine 类配准算法
2. Non-rigid 类配准算法
配准算法的 Tranformation 还需要一个迭代的优化过程(Optimization),从一个不太精确的配准到一个最优配准。优化过程为:
1. Rigid & Affine 类配准算法
1)Landmark-based regisitration:比如同一个人不同时期的图像发生了一些细微的变化,但仍然存在一些相对没有变化的点(下图中的红色点),通过找到这些特征点之间的对应关系,就能找到整幅图间的 transformation。通过计算这些点之间的相关性,找到这些点的质心,甚至通过旋转这些点,使这些点之间的距离达到最小,来实现 tranformation。Landmarks 的类型包括: 1)Intrinsic 内部特征点,比如图像内部的解剖结构特征点;2)Extrinsic 外部特征点,比如在对病人做成像前,人为地在其身体上标记一些很容易成像的点。
2)Surface-based regisitration:求取两幅图像对应的表面,通过计算并最小化两个表面间的距离来实现 tranformation。常用的基于表面的配准算法包括:1)The “Head and Hat” Algorithm;2)The Iterative Closest Point Algorithm(ICP),迭代式最近邻算法;3)Registration using crest lines。
3)Voxel intensity-based:通过计算图像间灰度的差异并最小化实现 tranformation。比如计算出要配准的两幅图像的灰度直方图(gray histogram),两个图间的灰度直方图称作 joint-histogram。当 joint-histogram 中间的白线越集中(相当于一致性分析),说明配准效果越好(joint-histogram 本身就可以作为一种测度来衡量配准的效果)。基于图像灰度配准的常用算法包括:1)Registration by minimizing intensity difference 最小化灰度差异;2)Correlation techniques 最大化相关性;3)Ratio image uniformity 最大化一致性比率;4)Partitioned Intensity Uniformity 图像部分间的灰度统一性。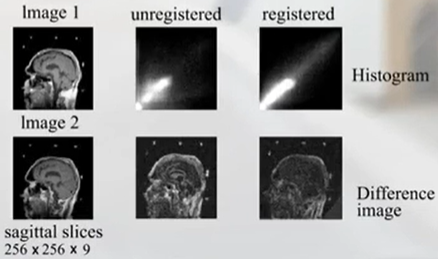
4)Information theory based:信息论里有熵、互信息等概念,都是用于衡量信息多少的标准。可以通过最大化两幅图像中共享信息的最大值来实现最优配准。基于信息论的常用算法包括:1)Joint entropy 相关熵,衡量两幅图像混合之后信息量的总和,信息量越小说明配准效果越好,也就是要求最小值来获得最优配准;2)Mutual information 互信息,衡量用一幅图像描述另一幅图像能够有多好,也就是看两幅图像是不是达到了最优的匹配,通过求最大值来获得最优配准;3)Normalized Mutual Information 正规化互信息,和基于互信息的方法思想一样。
2. Non-rigid 类配准算法
1)Basis functions:利用基函数可以很好地表达形变场,例如用傅里叶基函数/三角基函数(Fourier/trigonometric basis),小波基函数(wavelet basis)。使用基函数来处理优点在于可以很好地实现平滑约束。
2)Splines:在两幅图像中求取一些 control points(CPs),通过样条函数表达 CPs 间的差异来实现配准。
3)Physics-based:将变形过程看作一种物理形变过程,主要包括以下几种:1)Elastic Regisitration:线弹性配准,由 internal force 和 external force 共同促进,可以通过 Navier linear elastic patial differential equation(Navier 线弹性偏微分方程)来描述;2)Fluid Regisitration:基于流体场的配准;3)Mechanical models:通过机械模型的形变实现图像的配准;4)Optical flow:利用光流场实现配准。
求优过程就是对配准过程中 Transformation 参数最优化的过程。通过对目标函数(objective function)求最大/最小值,实现参数的最优化。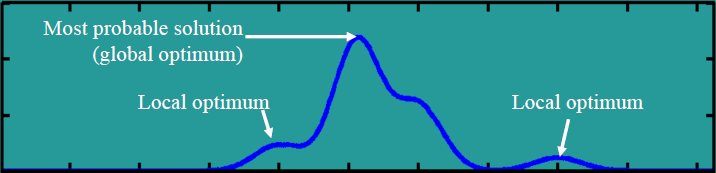
常用的目标函数包括:
以 Mean squared difference 为例,在图像 A 和 B 上找到相对应的点并计算灰度值的差异 D i f f e r e n c e ( i n d e x ) = A ( i n d e x ) − B ( i n d e x ) Difference(index) = A(index)-B(index) Difference(index)=A(index)−B(index),计算图中所有对应点灰度值差异的平方并求和 S u m + = D i f f e r e n c e ( i n d e x ) 2 Sum += Difference(index)^2 Sum+=Difference(index)2,最后除所有像素的总数 M a t c h ( A , B ) = S u m / n u m b e r O f P i x e l s Match(A, B) = Sum / numberOfPixels Match(A,B)=Sum/numberOfPixels,就得到了整个图像的灰度差异性。
通过反复计算图中每个像素点的差异求优的方法属于一种 exhaustive search,虽然稳定但计算速度太慢。目前更常用的优化算法是梯度下降 Gradient Descent,可以大大减少计算量。
对变换模型进行估计,要解决的任务包括:1)选择映射模型的类型,2)映射模型的参数估计。映射模型的类型需要与 moving image 假定的几何变换类型、图像采集方法、配准所需精度相匹配。构建映射模型之后,moving image 就能够通过变形覆盖到 fixed image 上,且两幅图对应的控制点应该尽可能的接近。
映射模型根据它们所支持的数据量分类:
映射模型根据用于估计模型参数的控制点的重叠精度分类:
最常用的全局映射模型:低次的二元多项式。其相似变换也是最简单的形式,包括平移、选装和缩放。这种模型也被称作 “shape-preserving mapping”,因为它保留了角度的曲率,且由控制点明确规定了变换形式。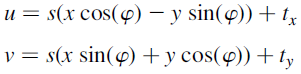
除此之外,还有仿射变换模型(仍属于线性模型):仿射变换模型可以将四边形映射到正方形上,模型由 3 个非共线控制点定义,以保留直线和直线平行度。
更复杂一些的就是 透视投影模型:该模型能够在保留直线的同时将四边形映射到正方形上,模型由 4 个独立的控制点定义。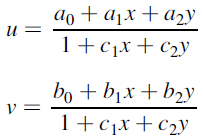
除以上列举的,还有二阶或三阶的多项式模型,但实际应用中不太使用这些高阶模型。因为在 moving image 与 fixed image 进行对齐时,高级模型可能会导致不必要的扭曲。通常,控制点的个数会多于确定映射模型所需的最小数量,通过最小二乘拟合映射模型的参数,使其能够最小化控制点的平方误差之和。
全局映射模型可能无法正确处理局部变形的图像,因此在图像发生局部几何失真的情况下,使用局部映射模型效果更好。加权最小二乘法(weighted least square)和加权平均法(weighted mean method)的变体:分段线性映射(piecewise linear mapping)【67】 和 分段三次映射(piecewise cubic mapping)【68】,都可以进行局部图像配准。
[todo]
[todo]
对两幅图像的配准效果进行定量评估比较难,因为没有 ground truth,不知道什么情况才是最优的配准效果。
有一种评估方法是,通过计算机模拟一个 model 实现评估。比如将一幅图人为地平移、旋转、放缩,这样我们就已经知道这幅图发生了什么变化,也就是知道 ground truth。接着让算法实现配准,看能不能达到理想的效果,但是临床上用这种方法衡量不太准确,仍然需要从视觉上进行衡量。还通过人工做一些 ground truth,或者通过解剖结构间的差异来估算。
医学图像中最经典的两种评估方法:
此外,在配准完成后需要向用户展示结果,常用的展示方法包括:
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删