《FLUENT 14自学手册》精要：流体运动与换热的数学基础

FLUENT 14流场分析自学手册

本节将给出求解多维流体运动与换热的方程组。

1 物质导数

把流场中的物理量认作是空间和时间的函数：

T=T(x,y,z,t) p=p(x,y,z,t) v=v(x,y,z,t)

研究各物理量对时间的变化率，例如速度分量u对时间的变化率：

式中的u、v、w分别为速度沿x、y、z三个方向的速度矢量。

将上式中的u用N替换，代表任意物理量，得到任意物理量N对时间t的变化率：

这就是任意物理量N的物质导数，也称为质点倒数。

2 不同形式的N-S方程

下面给出不同形式的N-S方程组：

由流体的黏性本构方程得到直角坐标系下的N-S（Navier-Stokes）方程：

如果忽略黏性的变化，认为黏性系数为常数时，方程式（1-32）简化为矢量形式的N-S方程：

在处理实际问题时，为提高边界附近数值计算的精度，常常使用贴体的任意曲线坐标系对方程求解。根据直角坐标系中建立的流体力学方程，可利用雅可比（Jacobian）理论导出任意曲线坐标系下的流体力学方程。忽略质量力后，在直角坐标系中流体力学方程的统一形式可写为：

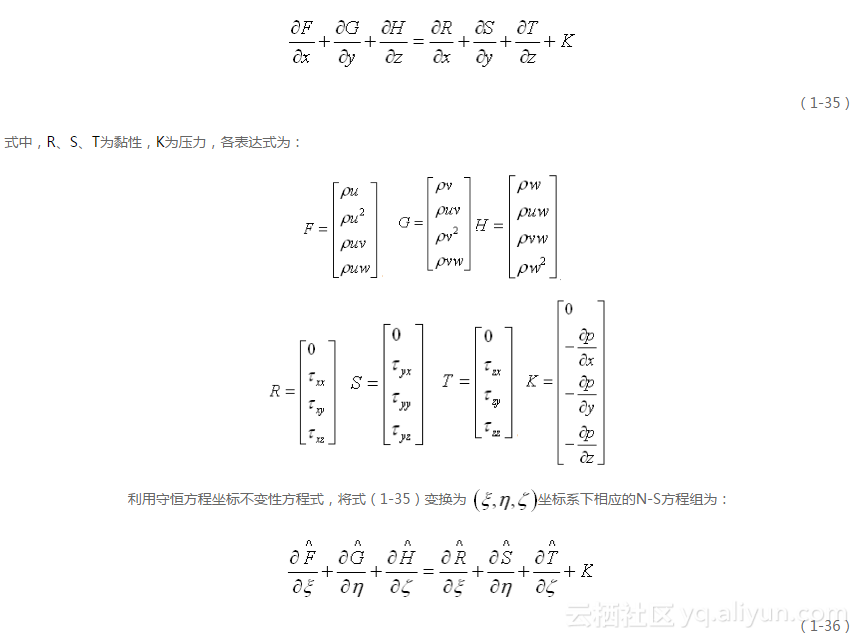
式中：

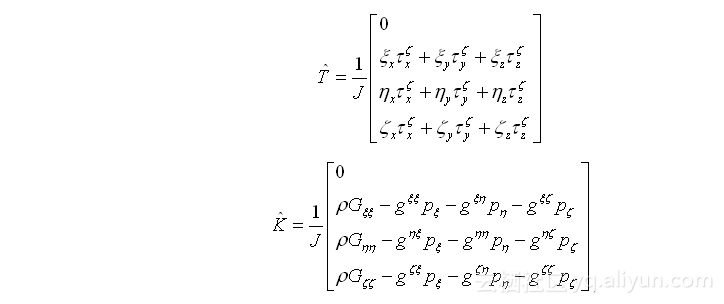
式中，J为雅可比行列式，其表达式为：

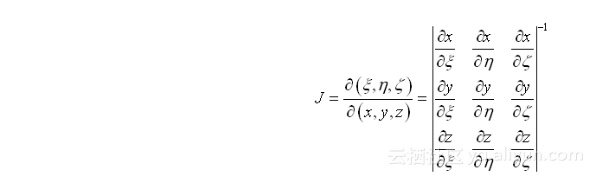
可压方程中，密度是参变量而不是常数，方程组中增添一个能量方程。忽略质量力、化学反应和辐射效应后，在直角坐标系中的雷诺平均N-S方程组为：

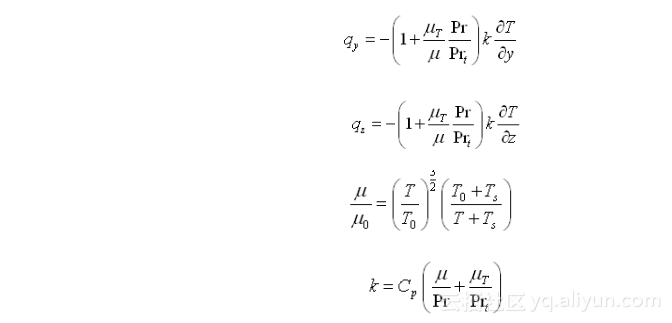
在以上各式中，Pr为普朗特（Prandtl）数，可取0.72。Prt为湍流普朗特数，取0.9。μ为分子黏性，由Sutherland公式确定。μ T为湍流黏性。k为导热系数。

3 能量方程与导热方程

描述固体内部温度分布的控制方程为导热方程，直角坐标系下三维非稳态导热微分方程的一般形式为：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删