《FLUENT 14流场分析自学手册》概览：流体运动基础

流体运动的基本概念

FLUENT 14流场分析自学手册

本节简要介绍流体运动的几个基本概念，这些概念都是有关流体运动的最基本的术语，读者有必要了解一下。

1 层流流动与紊流流动

当流体在圆管中流动时，如果管中流体是一层一层流动的，各层间互不干扰、互不相混的，这样的流动状态称为层流流动。当流速逐渐增大时，流体质点除了沿管轴向运动外，还有垂直于管轴向方向的横向流动，即层流流动已被打破，完全处于无规则的乱流状态，这种流动状态称为紊流或湍流。流动状态发生变化（从层流到紊流）时的流速称为临界速度。

大量实验数据与相似理论证实，流动状态不仅取决于临界速度，而是由综合反映管道尺寸、流体物理属性、流动速度的组合量—雷诺数来决定的。雷诺数Re定义为：

式中，d为管道直径，V为平均流速，μ为动力黏性系数。

由层流开始转变到紊流时所对应的雷诺数称为上临界雷诺数，用 $\operatorname{Re} _{cr}^' $ 表示；由紊流转变到层流所对应的雷诺数称为下临界雷诺数，用Recr表示。通过比较实际流动的雷诺数Re与临界雷诺数，就可确定黏性流体的流动状态。

（1）当Re

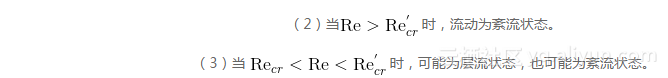
在工程应用中，取Recr=2000。当Re<2000时，流动为层流运动，当re>2000时，流动为紊流运动。

实际上，雷诺数反映了惯性力与黏性力之比，雷诺数越小，表明流体黏性力作用越大，能够减弱引起紊流流动的扰动，保持层流状态；雷诺数越大，表明惯性力对流体的作用越明显，易使流体质点发生紊流流动。

2 有旋流动与无旋流动

有旋流动是指流场中各处的旋度（流体微团的旋转角速度）不等于零的流动，无旋流动是指流场中各处的旋度都为零的流动。流体质点的旋度是一个矢量，用ω表示，其表达式为：

若ω=0，则称流动为无旋流动，否则为有旋流动。

流体运动是有旋还是无旋，取决于流体微团是否有旋转运动，与流体微团的运动轨迹无关。流体流动中，如果考虑黏性，由于存在摩擦力，这时流动为有旋流动；如果黏性可以忽略，而流体本身又是无旋流，如均匀流，这时流动为无旋流动。例如均匀气流流过平板，在紧靠壁面的附面层内，需要考虑黏性影响。因此，附面层内为有旋流动，附面层外的流动，黏性可以忽略，因此可视为无旋流动。

3 声速与马赫数

声速是指微弱扰动波在流体介质中的传播速度，它是流体可压缩性的标志，对于确定可压缩流的特性和规律起着重要作用。声速表达式的微分形式为：

当声音在气体中传播时，由于在微弱扰动的传播过程中，气流的压强、密度和温度的变化都是无限小量，若忽略黏性作用，整个过程接近可逆过程，同时该过程进行得很迅速，又接近一个绝热过程，所以微弱扰动的传播可以认为是一个等熵的过程。对于完全气体，声速又可表示为：

式中，k为比热比，R为气体常数。

上述公式只能用来计算微弱扰动的传播速度。对于强扰动，如激波、爆炸波等，其传播速度比声速大，并随波的强度增大而加快。

流场中某点处气体流速V与当地声速c之比称为该点处气流的马赫数，用Ma表示，其表达式为：

马赫数表示气体宏观运动的动能与气体内部分子无规则运动的动能（即内能）之比。当Maleqslant0.3时，密度的变化可以忽略，当Ma>0.3时，就必须考虑气流压缩性的影响。因此，马赫数是研究高速流动的重要参数，是划分高速流动类型的标准。当Ma>1时，为超声速流动，当Ma<1时，为亚声速流动，当ma≈1时，为跨声速流动，当ma>3时，为超高声速流动。超声速流动与亚声速流动的规律有本质的区别，跨声速流动兼有超声速与亚声速流动的某些特点，是更复杂的流动。

4 膨胀波与激波

膨胀波与激波是超声速气流特有的重要现象，超声速气流在加速时要产生膨胀波，减速时一般会出现激波。

当超声速气流流经由微小外折角所引起的马赫波时，气流加速，压强和密度下降，这种马赫波就是膨胀波。超声速气流沿外凸壁流动的基本微分方程表达式为：

当超声速气流绕物体流动时，在流场中往往出现强压缩波，即激波。气流经过激波后，压强、温度和密度均突然升高，速度则突然下降。超声速气流被压缩时一般都会产生激波，所以激波是超声速气流中的重要现象之一。按照激波的形状，可将激波分为以下3类。

1）正激波：气流方向与波面垂直。

2）斜激波：气流方向与波面不垂直。例如，当超声速气流流过楔形物体时，在物体前缘往往会产生斜激波。

3）曲线激波：波形为曲线形。

设激波前的气流速度、压强、温度、密度和马赫数分别为v 1，p 1，T 1，ρ 1和Ma，经过激波后突然增加到v 2，p 2，T 2和ρ 2，则激波前后气流应满足以下方程。

据此，可得出激波前后参数的关系：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删