正交试验分析：Minitab可视化教程

SPSS只能对试验设计的数据进行处理分析，尚不能进行试验方案的设计安排，这一点与Minitab相比，明显不足。

  某工厂希望提高产品转化率，想着从产品的生产工艺下手，经分析影响转化率的工艺可控因素有3个，反应温度、反应时间、加碱量，并研究确定每个因素取三个水平进行正交试验。

  3因素3水平，且不考察交互作用的情况下，L934正交表是最佳选择 。前三列分别安排三个因素，最后一列作为空列考察试验误差。

  利用Minitab创建L934正交表试验方案。

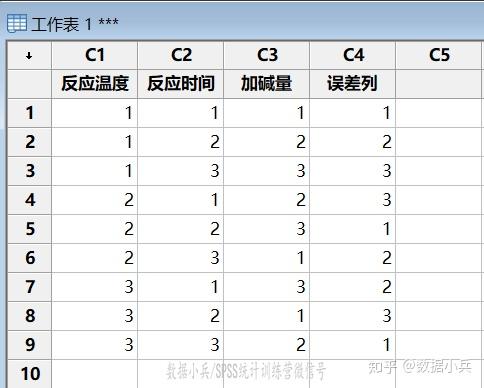
  然后呢，在9个处理中随机安排具体的实验次序，实施生产，记录产品转化率试验指标数据，将其录入至C5列。

  首先我们来看极差分析。

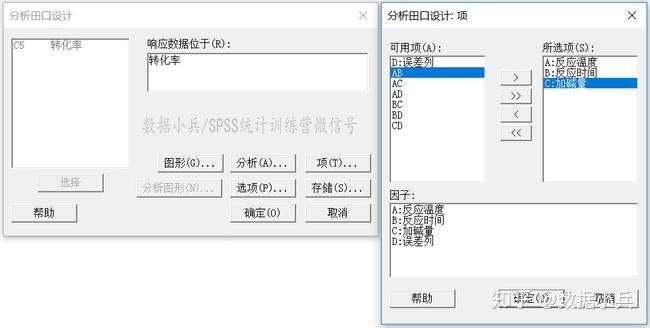
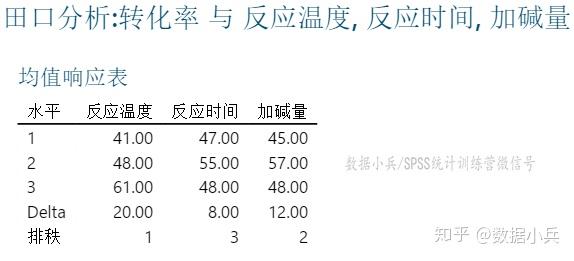
  此表中数据是因素各水平下转化率平均值，Delta一行的数据即为极差了。很明显 ，极差从大到小依次是：反应温度>加碱量>反应时间，也可以理解为三个试验因素的重要性顺序。

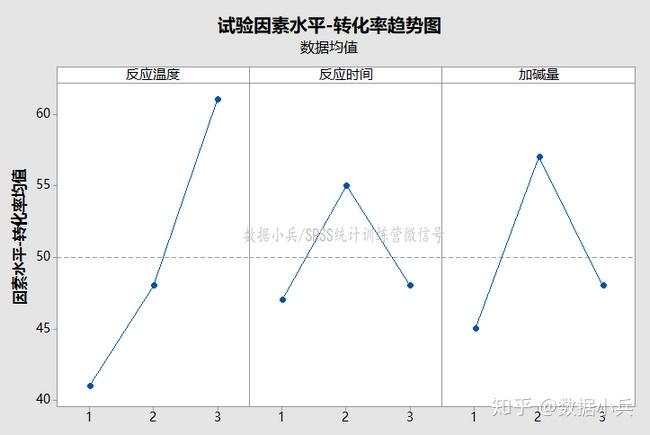
  上图是因素水平-转化率均值趋势图，美观、直观，试验指标Y望大，越大越好，所以各因素优水平也很明显，分别是A3、B2、C2。

  如果我们只使用极差分析来总结此处正交试验的结论 ，那么最优工艺组合是A3B2C2，该组合没有出现在已经实施的9个处理中，这恰好说明正交试验本身的科学性。

  如果我们想搞清楚三个试验因素对转化率的影响在统计学上是不是显著，那么接下来需要进行方差分析。

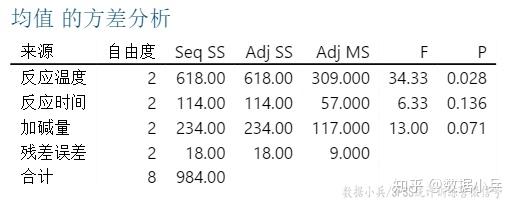
minitab方差分析表。最简单直接的解读方法是直接看最后一列，概率p值。我们发现仅反应温度的p值小于0.05，也就是说统计上认为反应温度对试验指标转化率有显著影响，统计上有意义。其他两个因素影响相对较小。

  还没有完。

  现在反应温度在统计上认为是一个相对很重要的因素，它下设3个水平，请问这3个水平差异表现如何？我们该选谁作为优水平呢？

  所以，需要多重比较。

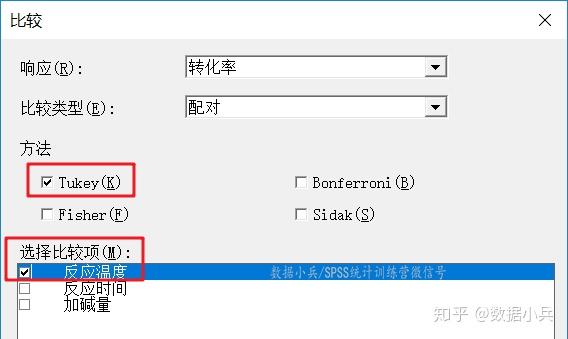
  这一步在minitab中比较麻烦，还需要再对试验数据进行一次【方差分析→一般线性模型】处理，然后单独进行一个多重比较的过程。这一点SPSS做得更高效一些。

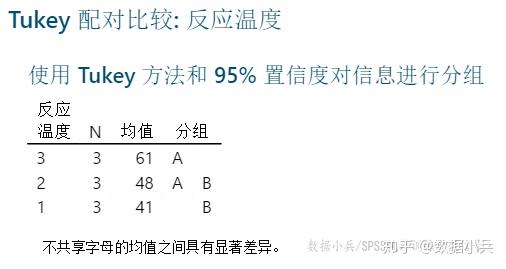
  minitab说的很清楚，不共享字母的均值之间具有显著差异，比SPSS子集比较更直接。显然反应温度的3个水平中，1水平和3水平下转化率均值差异是显著的，目标望大，所以该因素的有水平非3水平莫属。

  其他两个因素可以直接依据极差分析中的因素水平转化率均值来给定优水平，分别是B2和C2，至此，我们认为能使产品转化率达到最佳高度的工艺组合是A3B2C2。

  正交试验环节结束，后面可再安排部分验证试验以考察最优组合是否稳定。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删