LS-DYNA中有多种用于三维实体单元的混凝土本构模型,其中72号材料本构模型运用得比较广泛,本次研讨会主要介绍72号材料本构模型的原理、使用方法以及优缺点和适用范围。
1)压力敏感材料(如泥土、混凝土等)本构方程的基本特点
2)混凝土材料的典型力学特征
3)LS-DYNA混凝土本构72号模型的基本理论
a. 对混凝土典型力学性能的数值模拟
4)72号模型的LS-DYNA关键字及参数设定
a. 参数自动生成方式
b. 用户定制输入方式
5)72号模型的数值表现
a. 单一单元的响应
i. 单轴拉伸及压缩
ii. 三轴拉压
iii. 循环加载
b. 结构模型的响应
i. 三轴受压
ii. 冲击波响应
iii. 冲撞侵彻响应
6)总结72号模型的优缺点及适用范围

材料本构本质上为应力应变关系,如胡克定律也是应力应变关系。简单来说F=kx( k代表刚度),或σ=Eε(杨氏模量*应变),该定律仅适用于纯弹性材料。从材料的响应角度,材料有弹性和塑性之分。弹性是指如果没有变形,就没有应力;反之亦然。
而塑性变形指,当应力消失后,仍然会有永久的变形,该情况则不适用胡克定律。由此弹塑性材料模型应运而生,首先要决定在变形过程中塑性变形的量,然后要决定在当前变形下的材料强度,及应力状态。简言之,在胡克定律基础之上,应力等于刚度乘以弹性应变(弹性应变指总的应变减去塑性应变),材料的强度,如各项同性硬化的弹塑性,上图中底部公式包含的三个变量分别为初始强度,硬化系数,塑性应变。

任何材料的强度都不是无限的。因此严格来说并不存在真正的弹性材料,都具有一定的强度、且到一定的时候都会被破坏。对于压力不敏感材料,尤其是金属类材料,上图中前两行公式为典型的两个屈服函数或屈服准则。屈服函数需满足条件:综合应力状态减去强度后小于等于零,小于零代表弹性状态,等于零代表塑性状态,不存在大于零的情况。
如何保证等式小于或等于零?材料在加载的过程当中应力状态持续变化,如加载到第n+1步(第n步加上第n+1步的增量)时,若材料已进入塑性状态,则屈服函数在第n+1步或第n步都等于零,该方程可以理解为泰勒公式展开后去掉高阶项,此时得到材料的强度。除了一致性条件外(进入塑性后,每一步都等于零),还需要满足流动准则:该流动准则定义塑性流动的方向,及塑性应变的增量。
塑性式函数比屈服函数多了参数ω(ω等于1时代表金属材料-关联塑性流动)。对于混凝土来说,ω不等于1代表没有关联none associative。上图中右下角代表应力应变关系,当前为弹性变形计算时,下一步应变增量(无法确认是弹性还是塑性),实际处理时会先默认为弹性。该情况下应力应变为线性关系,F(σ)方程会大于零,确定当前为塑性变形、并拉回到屈服面上。每类材料都有不同的屈服面,屈服面定义该材料的强度,由于材料的强度是有限的,最终回到强度面上,数值上表现为F函数小于等于零。

通过计算得出塑性变形的增量。假设当前步的变形为弹性变形,Δεn+1为当前步的应变增量,先把它认为全部都是弹性变形,相应的应力就是上一步的应力加上当前的应力增量。然后计算得到塑性应变增量,有了塑性应变增量之后进行:
(1)更新当前步的应力σn+1;
(2)更新塑性应变ε;
(3)更新材料强度。硬化指数ET乘以当前等效应变的增量。

上文所提均为压力不敏感材料(主要指金属材料)。对于压力敏感材料,通用表达式(屈服函数)中有压力项I1,I1指应力的第一不变量,即1/3的正应力的和。J2、J3代表应力偏量的第二和第三不变量。图中第二行公式为最大拉伸应力理论,θ与J3相关,图中第二行公式为莫尔准则,C是材料的粘度,Φ是内摩擦角。图中第三行公式Drucker-Prager准则,也是一类压力敏感材料的材料本构。

Ottosen model有四个参数a,b,k1,k2。LS-DYNA的84材料本构基于该模型。Hsieh-Ting-Chen model含有4个参数A、B、C、D。Drucker-Prager,Mohr criterion在LS-DYNA中多应用于泥土材料(非混凝土)。
Ottosen model四个参数由四个实验确定。由于Ottosen model的参数与混凝土本身的抗拉强度和抗压强度的比值相关,有一定范围(上图中表格所示),通常在10%。对于Hsieh-Ting-Chen model,通过一些实验,可以确定4个参数A、B、C、D的量(图中右下角所示),可以看出这四个参数与混凝土强度没有相关性,很可能该模型并非十分精确的模型,也正是因为存在局限性,而不适用于商业软件。
Willam-Warnke Five-parameter Model是一个5参数模型,拉伸子午线Tensile meridian及抗压子午线Compressive meridian相交必在同一个点,在Hydrostatic axis静水压力轴上,因此要求a0=b0。该模型在LS-DYNA中的*MAT_72或*MAT_159有借鉴,但与此并非一样的模型。由于该模型参数与材料的强度没有相关性,应用存在局限性。

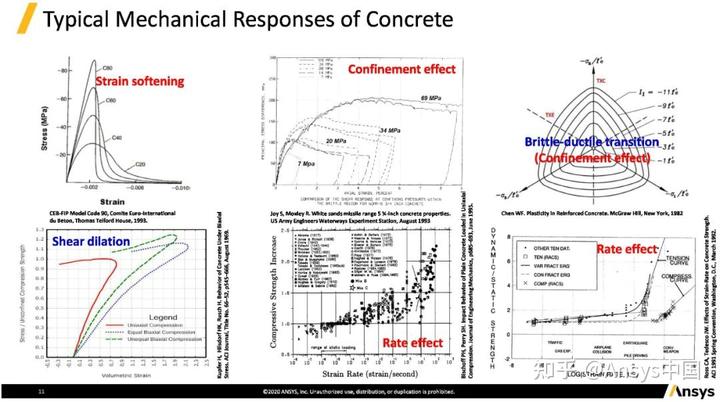
与金属等材料相比,混凝土有其典型性质。
首先,混凝土有应变软化的现象,当强度加载加到最大时若继续施加,承载能力会显著下降。
其次,围压效应(在混凝土块边上施加静水压力),围压对混凝土强度有显著影响。以上图中Confinement effect图表为例,若围压为0,受压到达最大强度后,迅速降为零;若施加7 Mpa围压,则承载能力显著提升;当围压增加到70 Mpa时,该材料的性质类似弹塑性材料,软化现象不再明显。右图展示了围压的效应,为主应力空间,对于金属材料表现为接近一个圆,而对于脆性材料来说更接近三角形,混凝土并不是完整的三角形(因为半脆性的缘故),混凝土随着围压的增加会越来越接近一个圆(外圈),外圈越接近塑性材料(脆性向塑性的转变)。
第三,剪切膨胀。对混凝土施加压力,初始混凝土体积随着施压压力而变小,当压力增加到一定程度之后,混凝土体积却开始膨胀。如上图中左下图表体积应变所示,体积应变为正时表示受压,红线逐渐变为负时,表示混凝土体积在变大。剪胀对于围压的效应至关重要。第四,对应变率的敏感。上图中Rate effect图表展示对受压应变率的不同响应,可以看到在应变率较高时(如100),抗压强度提高到2.2~2.3倍(也有一定上限)。右边Rate effect图表可以看到受拉曲线对应变率的敏感性特别高,(应变率2/s时强度到8),混凝土受拉时的应变率更为明显。


*Mat72R3基于LS-DYNA中*Mat_16的模型进一步开发而来(*Mat_16建议不再使用),主要用于模拟钢筋混凝土结构对高速动态载荷的响应。基本特征有:
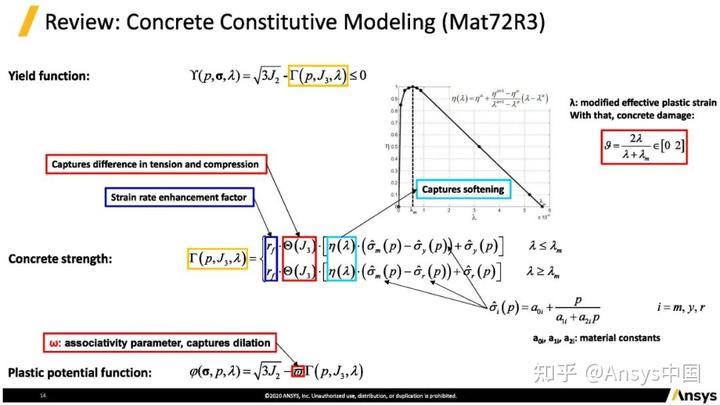
Mat72R3材料本构基本理论。通用混凝土本构的屈服函数Yield funtion,黄色框内项表示当前的材料强度。任何材料本构的等效应力减去强度均应小于等于0。拆分开第一项(图中深蓝色框)来捕捉应变率效应。第二项(红色框)捕捉混凝土在拉伸和受压方面的不同响应。第三项(浅蓝色框)捕捉混凝土软化。参数λ相当于等效塑性应变的函数。等式最右边几项是混凝土72号模型里的强度面。上图中第三个为(最下面的红框)塑性流动函数,参数ω可以捕捉混凝土的剪切膨胀。若ω为0(少数情况下),说明在72号模型里混凝土不会有剪切膨胀。

上图中参数rf为应变率效果。Plastic strain rate方程塑性应变的增量率ε ̇p。通过塑性应变的张量,可以算出等效塑性应变增量ε ̅ ̇^p,系数h也会影响应变率的放大因子rfc、rft。若需要在设计材料卡片时单独定义应变率曲线,可参考最后两组等式DIF(compression)、DIF(tension),这是应变率定义,需要整合成一条曲线,受拉是正的,受压是负的,作为应变率曲线的输入。

捕捉受拉和受压的不同。Θ (J3)函数与洛德角θ相关,洛德角即是J3也是J2的函数。参数ψ定义的拉伸子午线rt与受压子午线rc的比值。
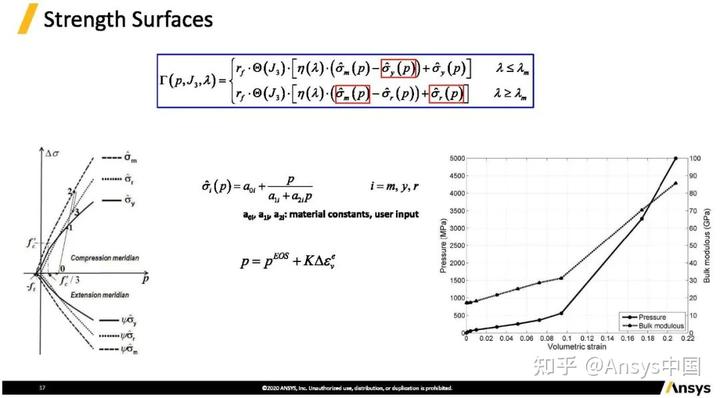
强度面,这里有有三个面σ ̂m为最大强度面maximum、σ ̂y为yield屈服强度面和σ ̂r为residual残余强度面。a_0i,a_1i,a_2i参数在材料卡里面定义,压力p在72号模型里面通过状态方程计算。如上图中右下图表所示,实线表示体积应变和压力的关系,虚线代表体积模量和体积应变的关系,这些参数LS-DYNA有自动输入可以直接使用。

确定塑性应变增量。首先假定当前的应变增量都是弹性的,基于此计算出应力增量,及推算当前的试应力。代入Trial yield function公式计算。Consistency condition一致性条件计算塑性应变的增量并更新。接下来需要确定:当前的材料强度、当前的应力状态,当前的塑性应变或材料的损伤。
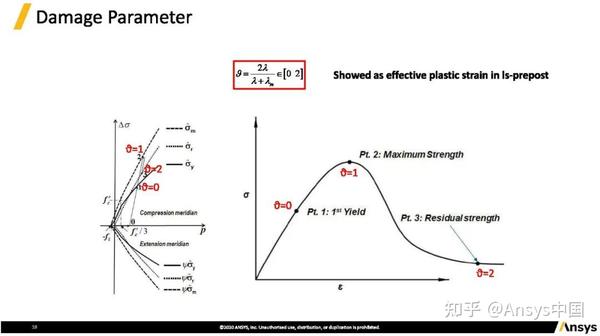
损伤函数,范围在0到2之间。如图所示在到达屈服面σ ̂y之前损伤函数值为0,逐渐增加到1(最大强度面σ ̂m),随后再回到2残余强度面σ ̂r。右图曲线为另外一种表达。

72号材料本构有48个参数,大多数LS-DYNA可以为用户自动生成。R0为密度,72号是基于英制单位进行开发的,RSIZE为长度单位的转换量(转换成英寸),UCF将当前压力单位转换成磅每平方英寸(RSIZE和UCF是需要用户填写的), 假如当前模型的单位为Gpa,1MPa=145000psi,LCRate为应变率,若应变率大于0,需要单独定义曲线来输入;若等于0,代表没有应变率;若等于-1,则程序会自动生成应变率曲线。

三个材料的最大强度面A0、A1、A2,若A0为负,则72号模型的其他参数可以自动生成,除单位转换外无需其他操作。若A0为正,则需要手动输入其他参数,否则系统默认为0。A0Y,A1Y,A2Y为屈服强度面参数,A1F,A2F是残余强度面参数。此外这些参数A0*\A1*\A2*有缺省值可用(该组缺省值基于45.4Mpa混凝土实验数据进行比例换算)。


Eta和lambda曲线需定义13个点,推荐使用程序自动生成的,用户也可以根据实验数据修改。B1用以控制受压的损伤,简单经验公式为b1=0.0135h+0.79(h为单元大小,单位是毫米才是这个表达式,如果是其他单位,用户自己做一下转换);B2用以控制受拉损伤,与单元大小无关,与材料受压强度有关, w_lz为材料的局部化距离(骨料的最大直径)。目前72号模型开发主要为计算混凝土的动态响应,更多研究的是受压,因此程序自动生成的B2不精确。B3 volumetric responses,为三项等压力的拉伸状态(实际受力很少出现,该参数可忽略)。程序生成的B1和B2不是特别的精确,用户可根据实验进行调整。

OMEGA(ω)关联度,影响剪切膨胀。在没有围压时,缺省值在0.5~0.75之间(缺省值为0.5,没有围压时建议最大可设置到0.75);有围压时,缺省值在0.8~0.9之间,建议有围压时用具体的实验标定一下。LOCWIDTH在程序中为三倍的最大骨料直径,推荐设置LOCWIDTH值小于一个单元尺寸,然后标定B1和B2。SLAMBDA为stretch factor拉伸系数,使用default 1.0即可,EDROP使用default 1.0缺省值(对响应影响不明显)。

除了自动生成的参数,也可以自己定义输入所有的参数。首先使用自动生成的输入运行任务后即停止任务,在生成的messag file中找到B1,将*MAT_CONCRETE_DAMAGE_REL3和*EOS_TABULATED_COMPACTION存成为一个新文件,作为直接输入信息,且可以根据需求修改其中的任何一个参数。

上列的每一个输入参数用户均可以修改。

状态方程EOS,蓝色框标注的VolStrain为体积应变,Pressure为压力,BulkUnld为卸载的体积模量,基本上这些状态方程中的数据无需改动。
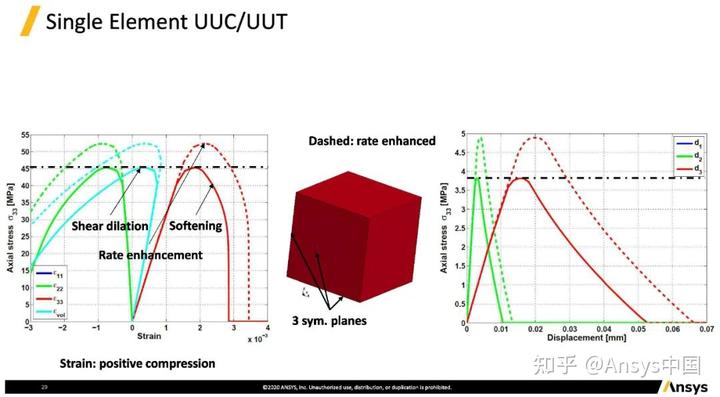
单个单元UUC/UUT。左图为单向受压,右图展示单向受拉。捕捉到软化,应变率效应,剪切膨胀。需要注意的是,为了达到真正的没有围压UUC/UUT,所创建的模型不能随便施加边界条件,因此该情况下,模型加了三个对称面,以使该单元在另外的三个面上可以自由移动,且没有任何围压效应,从而真正的做到了unconfined(无围压)。
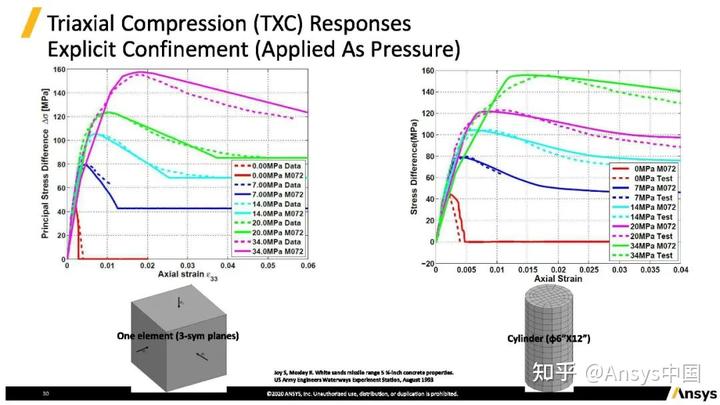
单个单元数值响应(左图)及结构响应(右图)。左图展示三向受压的情况(首先施加围压,然后在另外方向进一步加压),虚线是实验值。右图展示结构响应,这两种响应均与实验结果较好吻合。
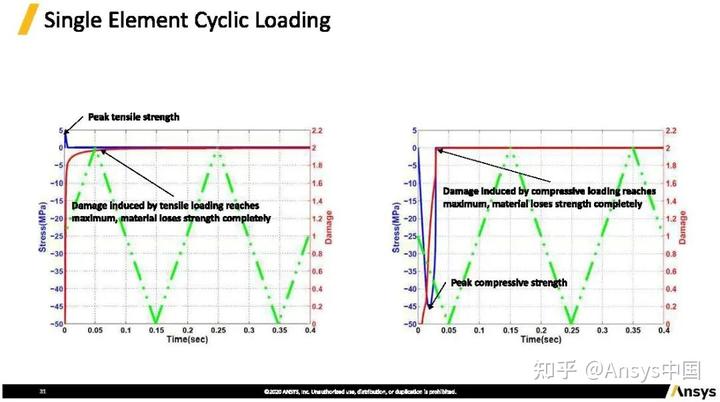
循环荷载,左图展示了由于受拉受压的效应——绿色折线的变化,在到达最大受拉应力后,材料出现软化,之后强度降为0。红色线段为损伤,最大值为2。当受拉达到一定程度的损伤后,此时材料被完全破坏,即使再进行反向加载受压的时候,不再有强度。该实验表明,只有一个标量的损伤函数的72号材料本构,并不适合做此类循环加载变形。右图展示在受压达到最大强度后,同样地,再继续加载的时材料出现损伤,再进行反向加载受压时也不再出现应力。只要损伤函数值到达2,材料强度基本消失。
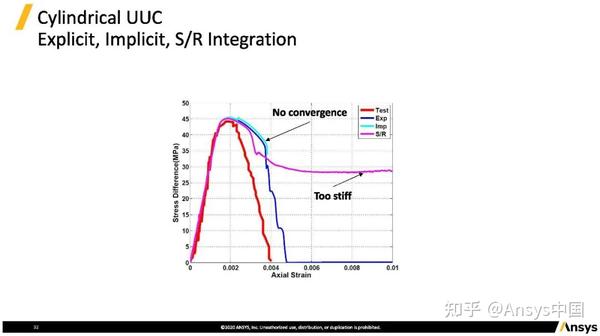
大部分情况下隐式计算对于72号不可行,若混凝土本身的变形不大可以尝试。有部分用户在计算动态响应时表示会出现沙漏,因而采用选择性缩减积分单元,但选择性缩减积分单元对于72号材料响应太强,因此不推荐使用该方式控制沙漏。

剪切膨胀对于围压效果通常通过某个结构来实现。如图所示,在圆柱外围添加一层CFRP或金属薄片。在轴向加载混凝土产生剪切膨胀时体积会变大,并对外围材料形成张力,此时张力在结构中会对材料形成一定压力(围压)。在对该结构进行离散成杆(将几层材料离散成杆单元)进行分析时,杆单元会受到张力,反过来的作用力就是所需的围压。
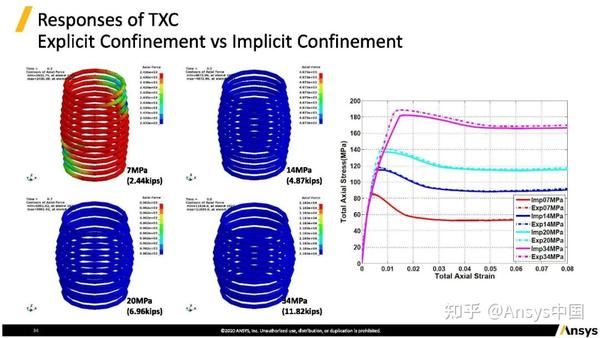
不同围压的情况下,当围压值为7 MPa,杆单元的轴向力约为2.44 kips;围压值为14 MPa,杆单元的轴向力约为4.87 kips;20 MPa围压,对应6.962 kips,34 MPa围压,对应11.82 kips。比较“隐式围压”和“显式围压”数值响应,两者相近,说明剪切膨胀的效果达到了预期围压效果。
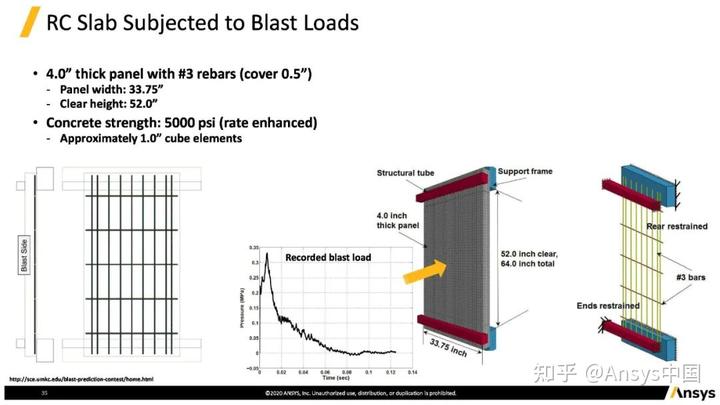
动态响应。对某钢筋混凝土板施加冲击波,以观测板的变形。
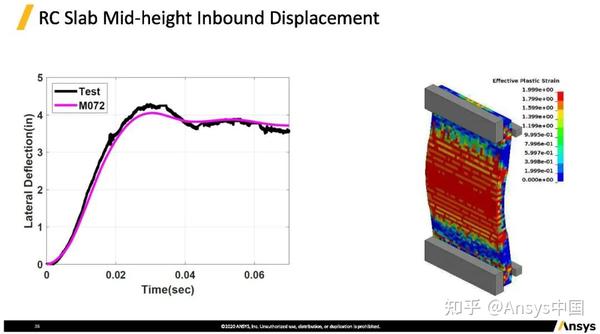
左图展示了钢筋混凝土板中间高度的位置的变形曲线,黑线为实验值,玫红色线为数值计算结果,可以看到吻合度较高。实验中横向偏转会达到最大值,随后小幅反弹,过中的反弹与实验还是有点差别,但材料本身结构总体响应基本上可靠,左图曲线的末端为最终的残余变形仿真与实验的对比,最终变形结果非常吻合。
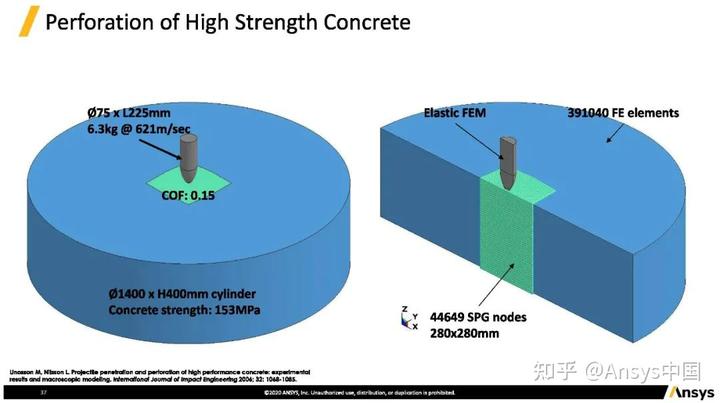
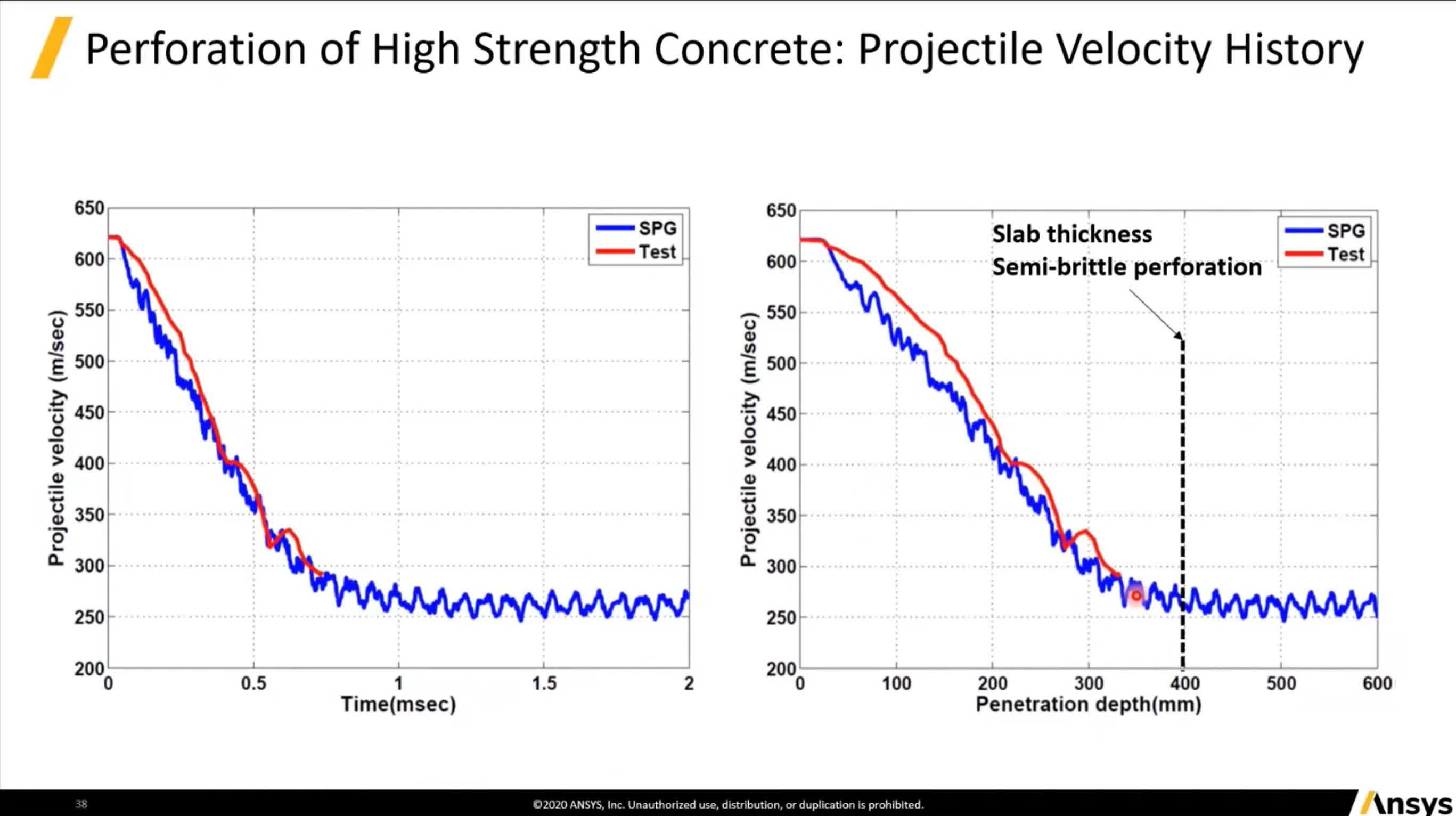
高速变形案例(子弹穿透153 MPa高强度混凝土)。该案例混凝土中间(绿色区域)使用SPG无网格方法计算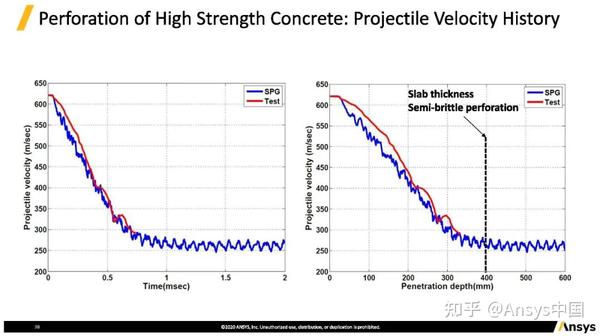
图中红色线段为实际实验中子弹的速度曲线,蓝色为SPG方法求解,两者吻合度非常高。案例中混凝土块厚度为400毫米,子弹在穿过400毫米以后速度基本稳定。该响应接近脆性响应,混凝土块本身并没有塑性变形,由于子弹穿过混凝土后不再有阻力。此外,混凝土仿真和实验中减速度(负的加速度)基本上是定值。
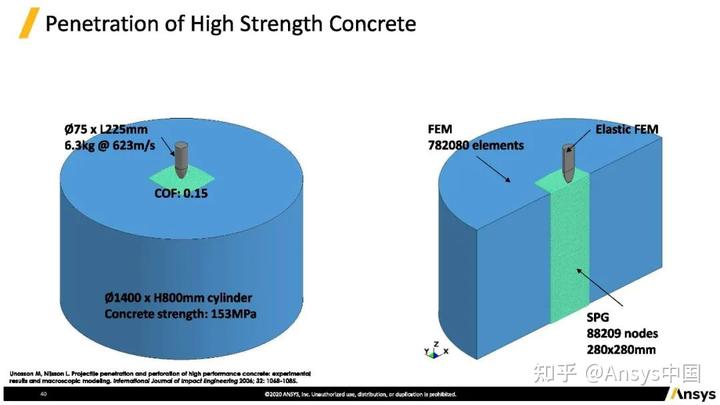
子弹侵彻厚度800毫米混凝土实验与仿真,中间绿色区域仍使用SPG无网格法。
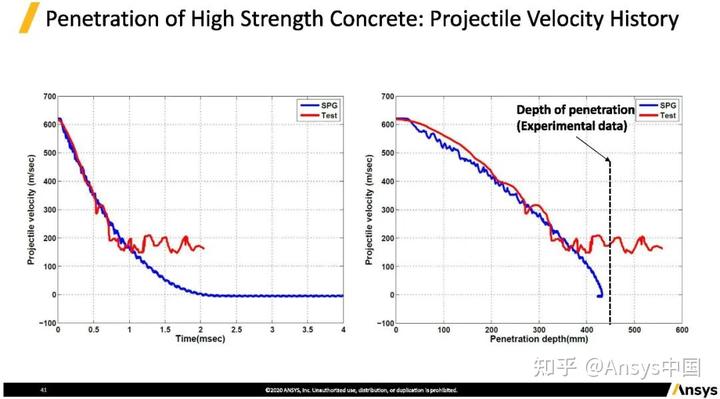
上图展示了实验曲线,到一定程度后实验曲线偏差逐渐增大,这是由于实验本身,能够观察到子弹会停留在混凝土中(最终速度应为0),但仪器却能测试到子弹速度,该处实验速度不再可靠。子弹停留之前的侵彻过程与实验相对吻合,实验中子弹的穿透深度约为450mm。仿真计算结果为430+mm,相对可靠。
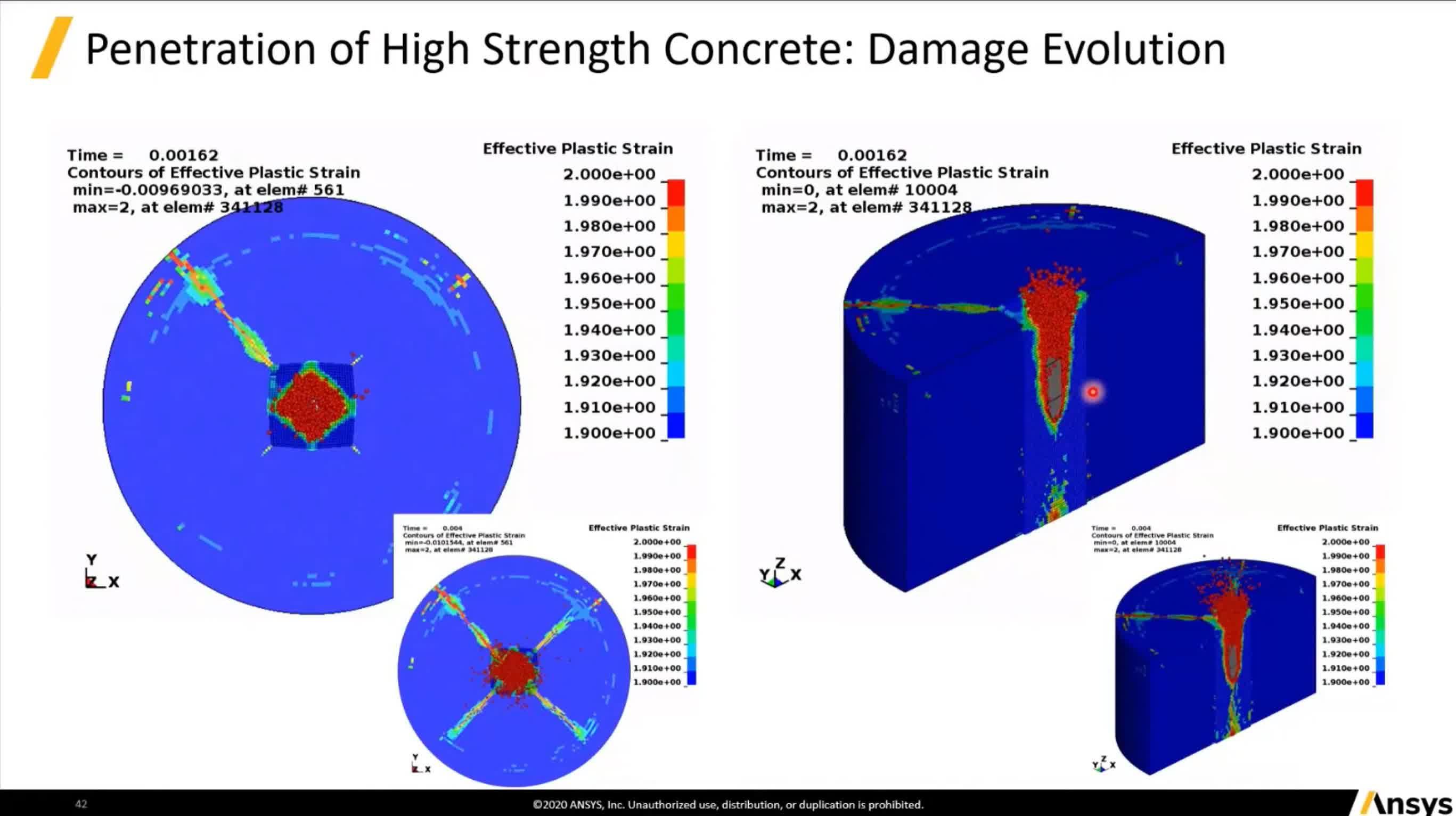
子弹侵彻混凝土的过程,最终混凝土裂成四块。
小结

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删