当物体运动遵循非线性状态方程或测量值是状态的非线性函数时，使用扩展卡尔曼滤波器。一个简单的例子是，当物体的状态或测量值是以球面坐标计算的，如方位角、海拔和范围。

状态更新模型

扩展的卡尔曼滤波公式将状态方程线性化。更新后的状态和协方差矩阵仍然是之前状态和协方差矩阵的线性函数。然而，线性卡尔曼滤波器中的状态转换矩阵被状态方程的雅各布矩阵所取代。 雅各布矩阵不是恒定的，而是可以取决于状态本身和时间。要使用扩展卡尔曼滤波器，必须同时指定状态转换函数和状态转换函数的Jacobian。

假设有一个预测状态的闭式表达式，作为之前状态、控制、噪声和时间的函数：

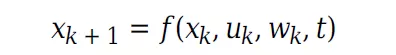
预测状态相对于前一状态的Jacobian为：

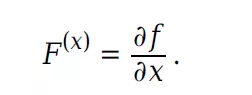
预测状态相对于噪声的Jacobian为：

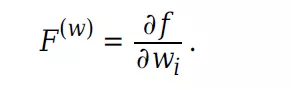
当噪声线性地进入状态更新方程时，这些函数采取更简单的形式:

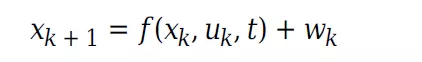
在此状态下:

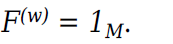
测量模型

在扩展卡尔曼滤波器中，测量可以是状态和测量噪声的非线性函数。

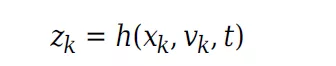
相对于状态的测量的雅各布值为          

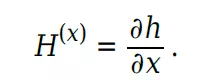
相对于测量噪声，测量的雅各布值为

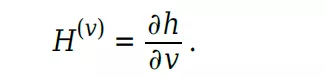
当噪声以线性方式进入测量方程时，这些函数采取更简单的形式:

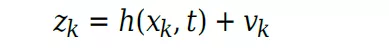
此时 ,

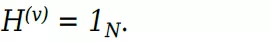
扩展卡尔曼滤波环路

这种扩展卡尔曼滤波环路与线性卡尔曼滤波环路几乎相同，只是。

- 尽可能使用精确的非线性状态更新和测量函数状态转换矩阵被状态雅各布取代

- 测量矩阵由相应的雅各布代替。

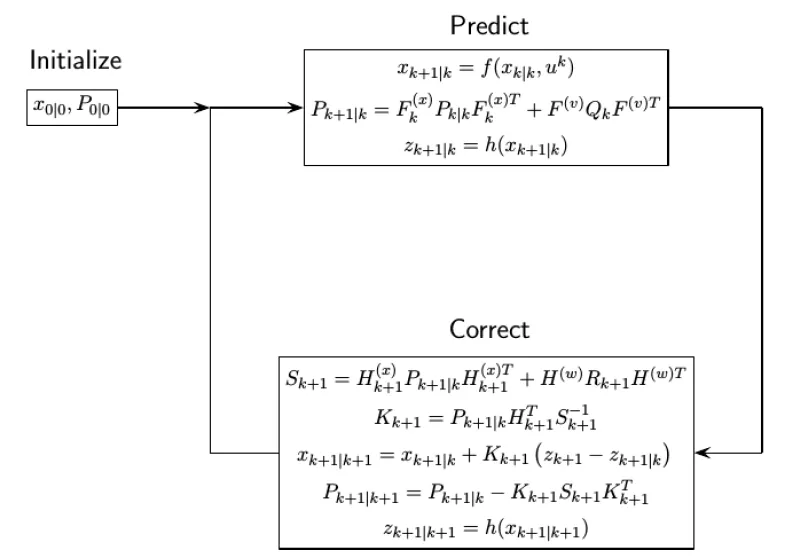
预定义的扩展卡尔曼滤波函数

自动驾驶工具箱提供了预定义的状态更新和测量功能，用于扩展卡尔曼滤波器。

trackingKF 函数实例：

创建一个二维追踪EKF对象，并使用名-值对来定义StateTransitionJacobianFcn和MeasurementJacobianFcn属性。使用预定义的恒速运动和测量模型以及它们的雅各布系数。

EKF = trackingEKF(@constvel,@cvmeas,[0;0;0;0], ...
           'StateTransitionJacobianFcn',@constveljac, ...
           'MeasurementJacobianFcn',@cvmeasjac);

运行过滤器。使用预测和纠正函数来传播状态。你可以按任何顺序调用预测和纠正，次数不限。在笛卡尔坐标中指定测量。

measurement = [1;1;0];
[xpred, Ppred] = predict(EKF);
[xcorr, Pcorr] = correct(EKF,measurement);
[xpred, Ppred] = predict(EKF);

[xpred, Ppred] = predict(EKF)

xpred = 4×1

   1.2500
   0.2500
   1.2500
   0.2500

Ppred = 4×4

  11.7500    4.7500         0         0
   4.7500    3.7500         0         0
        0         0   11.7500    4.7500
        0         0    4.7500    3.7500

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删