本节我们将介绍与矩阵相关的一系列运算,包括:调用函数运算、算术运算、关系运算、逻辑运算和集合运算。
在上一章中,我们介绍了常见的数学运算函数,例如abs, sin, round, log等。这些函数可以直接应用到矩阵上,所表示的含义是:对矩阵中的每个元素分别运用这些数学运算函数,因此返回的结果也是一个矩阵。下面我们来举几个例子:
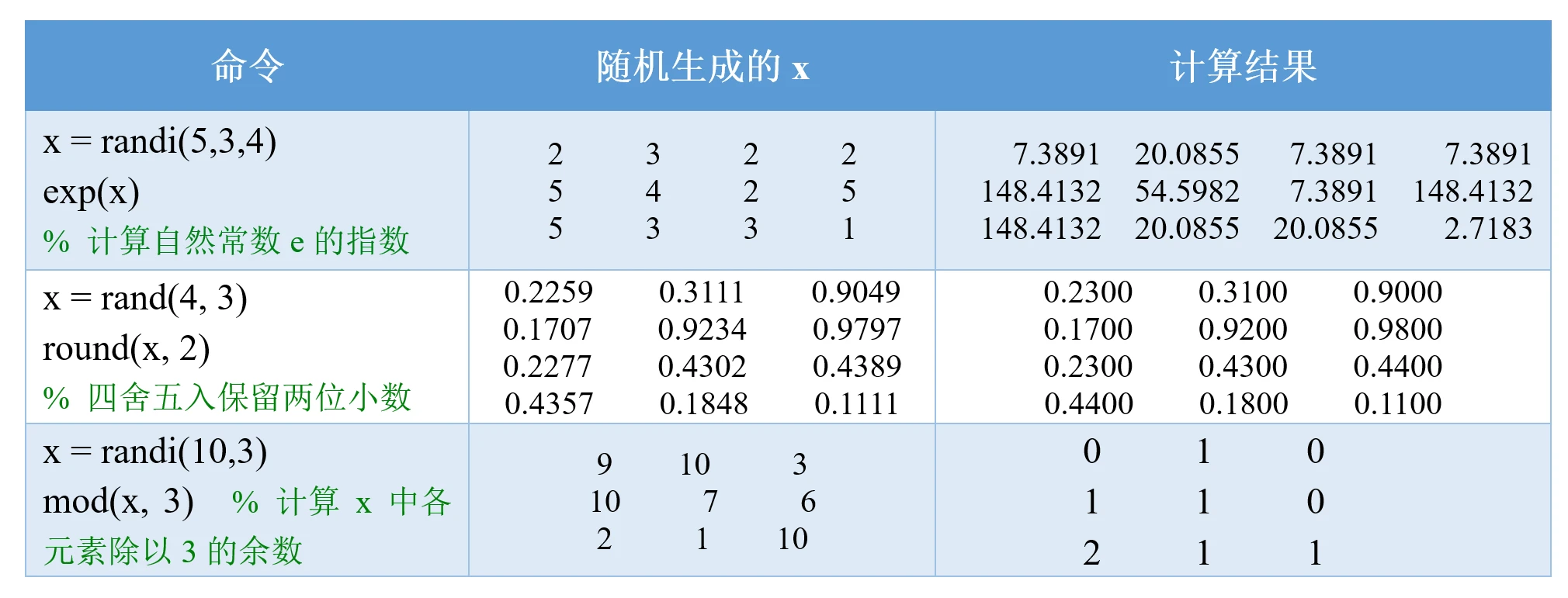
除了这些最基础的数学运算函数外,这一小节我们还要学习下表这些使用频率较高的函数,大家需要熟练掌握它们的用法:
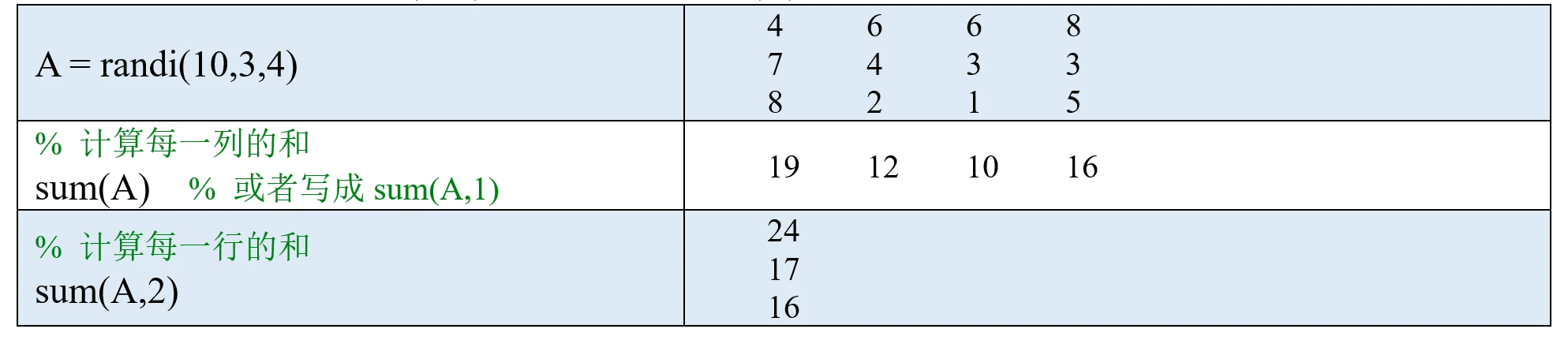
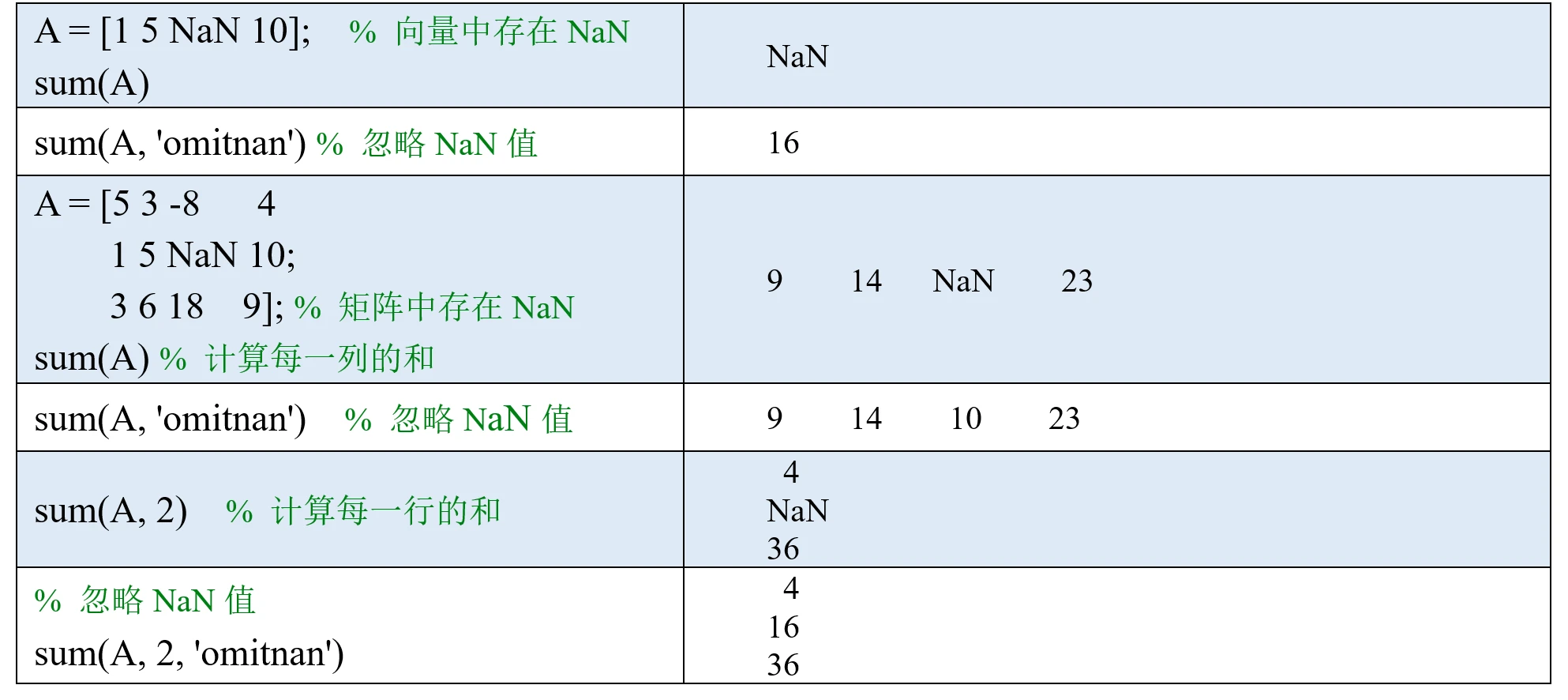
(1)如果A是一个向量,则sum(A)可以计算A中所有元素的和。

(2)如果A是一个矩阵,则sum(A,dim)可以计算A矩阵沿维度dim中所有元素的和。
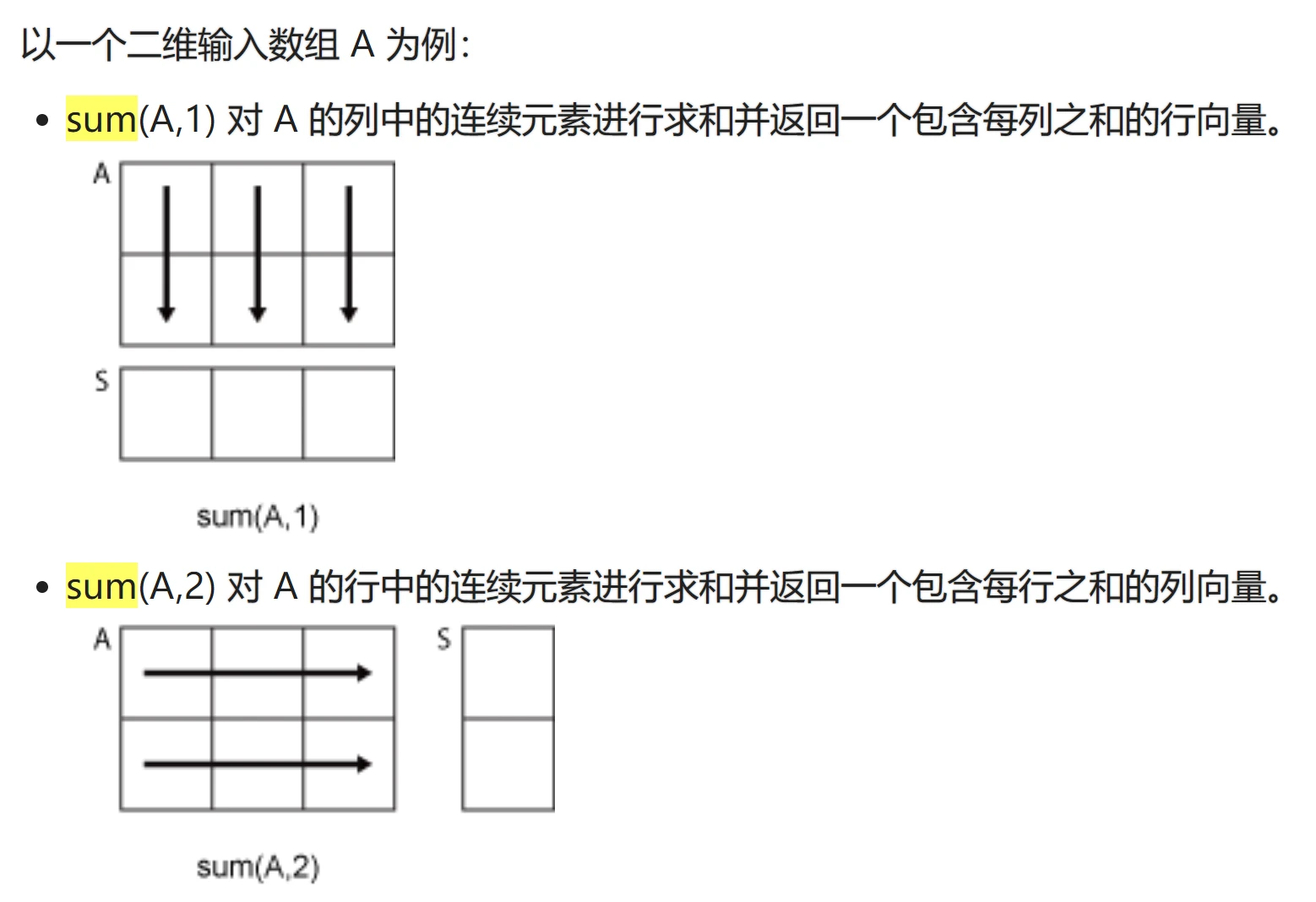
当dim = 1时,sum(A,1)可以简写成sum(A). (sum函数的帮助文档上有一个示意图)
官方文档上的截图:
(3)计算一个矩阵中所有元素的总和。
可以先用一次sum函数计算矩阵A每一列的和,返回一个行向量;然后再用一次sum函数计算这个行向量的和;也可以先使用A(:)语句把A中的所有元素按照线性索引的顺序拼接成一个向量,然后直接计算这个向量的和。

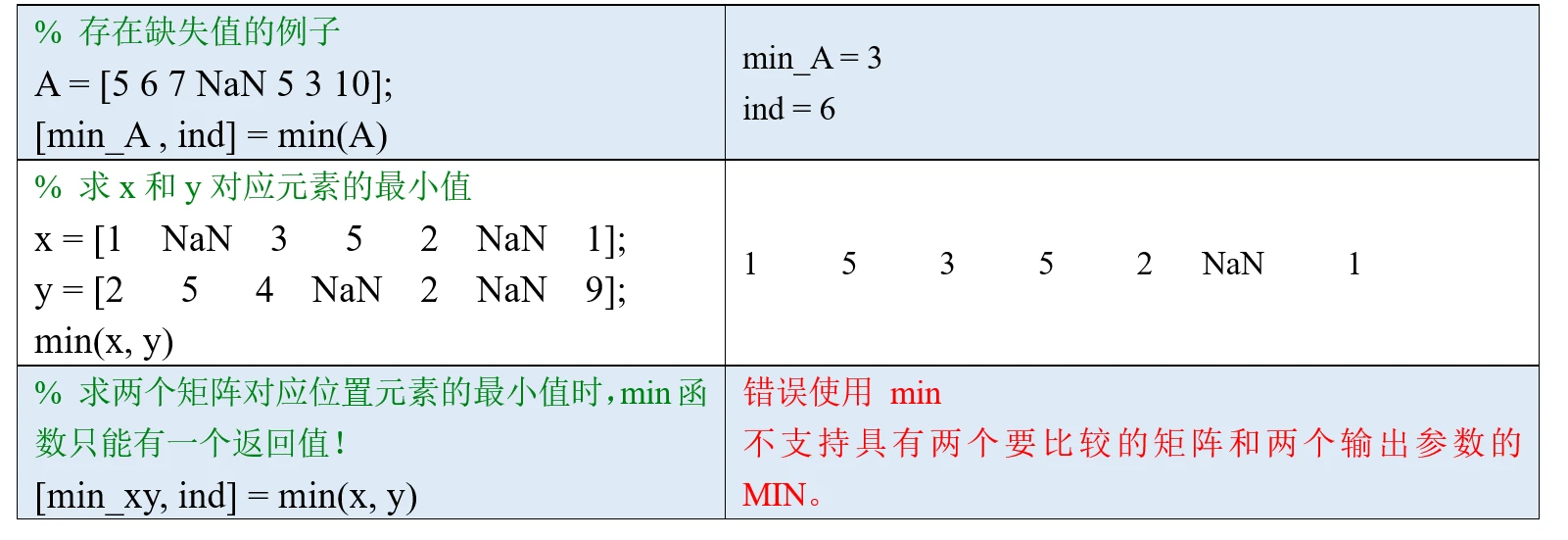
(4)指定如何处理NaN值
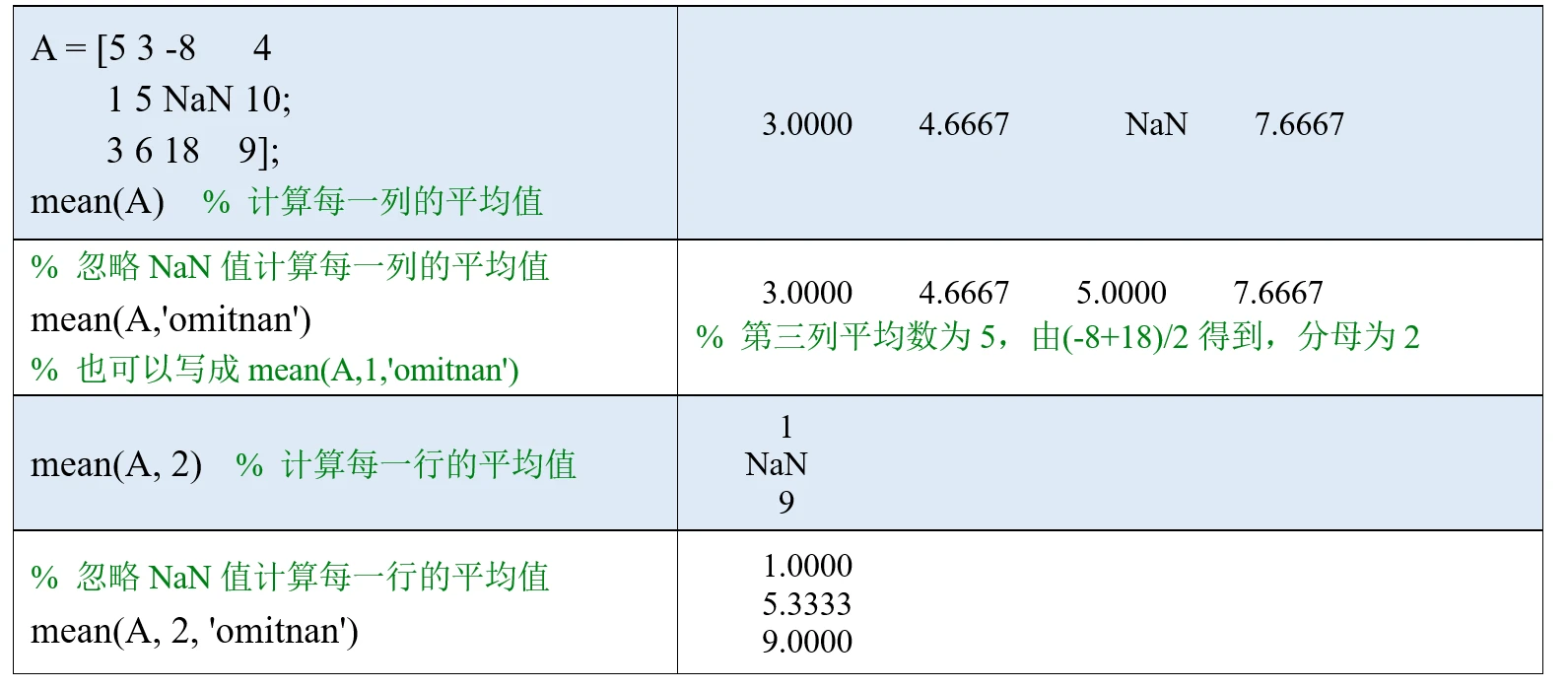
NaN指不定值或缺失值(Not a Number)。默认情况下,求和时有一个元素为NaN值,那么最终的和也为NaN;我们可以在最后加一个输入参数: 'omitnan', 这样计算时会忽略NaN值。
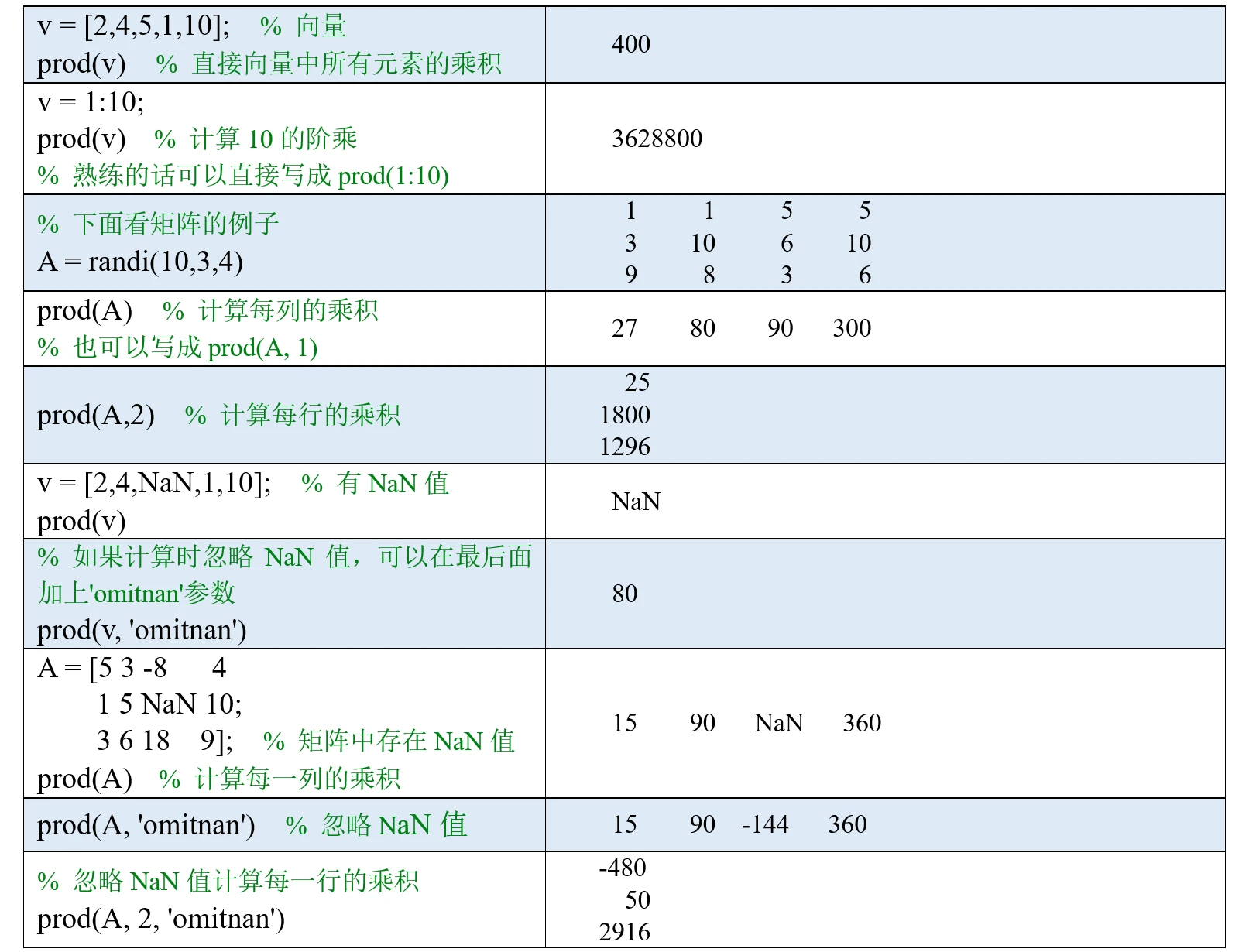
prod函数的用法和sum函数的用法相同,它是用来计算乘积的,我们直接来看例子。
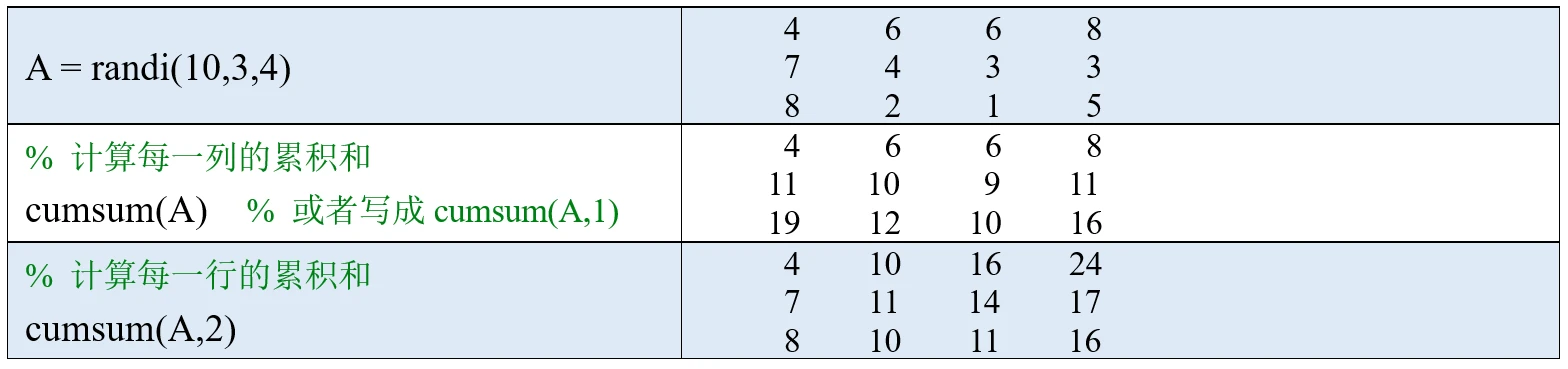
(1)如果A是一个向量,则cumsum(A)可以计算向量A的累积和(累加值)。

(2)如果A是一个矩阵,则cumsum(A,dim)可以计算A沿维度dim中所有元素的累积和,具体的使用方法和sum函数类似。
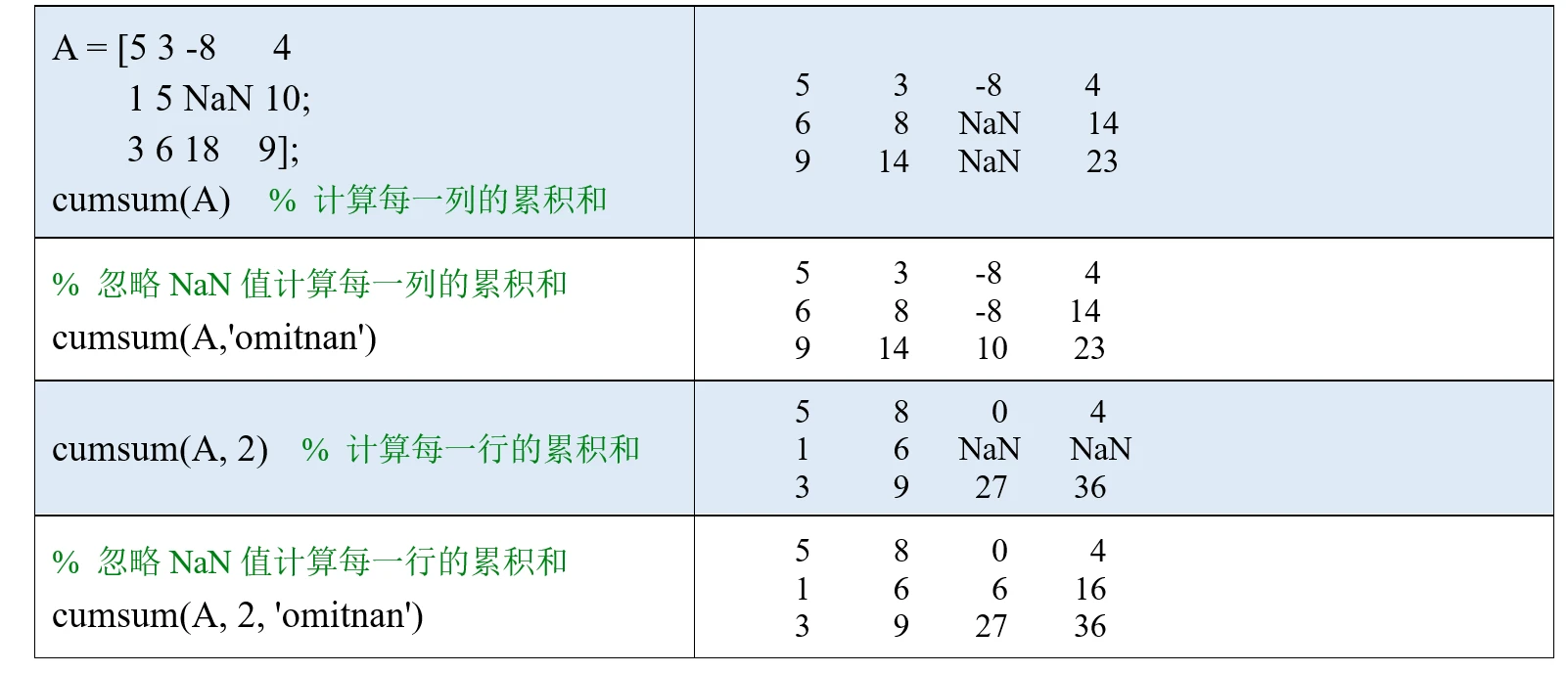
(3)也可以在最后加一个输入参数: 'omitnan', 这样计算时会忽略NaN值。
差分运算在和时间相关的数据中用的比较多。在原始序列中用下一个数值减去上一个数值可以得到一个新的序列,这个过程就是一阶差分;在一阶差分结果的基础上再进行一次一阶差分,就是二阶差分,举个例子,下表是清风老师8年来的体重变化,我们可以计算一阶差分和二阶差分的结果:

MATLAB中计算差分的函数是diff,我们可以使用diff(A,n)命令计算向量A的n阶差分,当n等于1时,可以直接写成diff(A).

diff函数也可以用在矩阵上面:diff(A,n,dim)表示沿矩阵A的维度dim方向上计算差分,当dim=1时沿着行方向计算,即得到每列的n阶差分;当dim=2时沿着列方向计算,即得到每行的n阶差分。类似的,dim=1时,diff(A,n,1)也可以简写成diff(A,n).
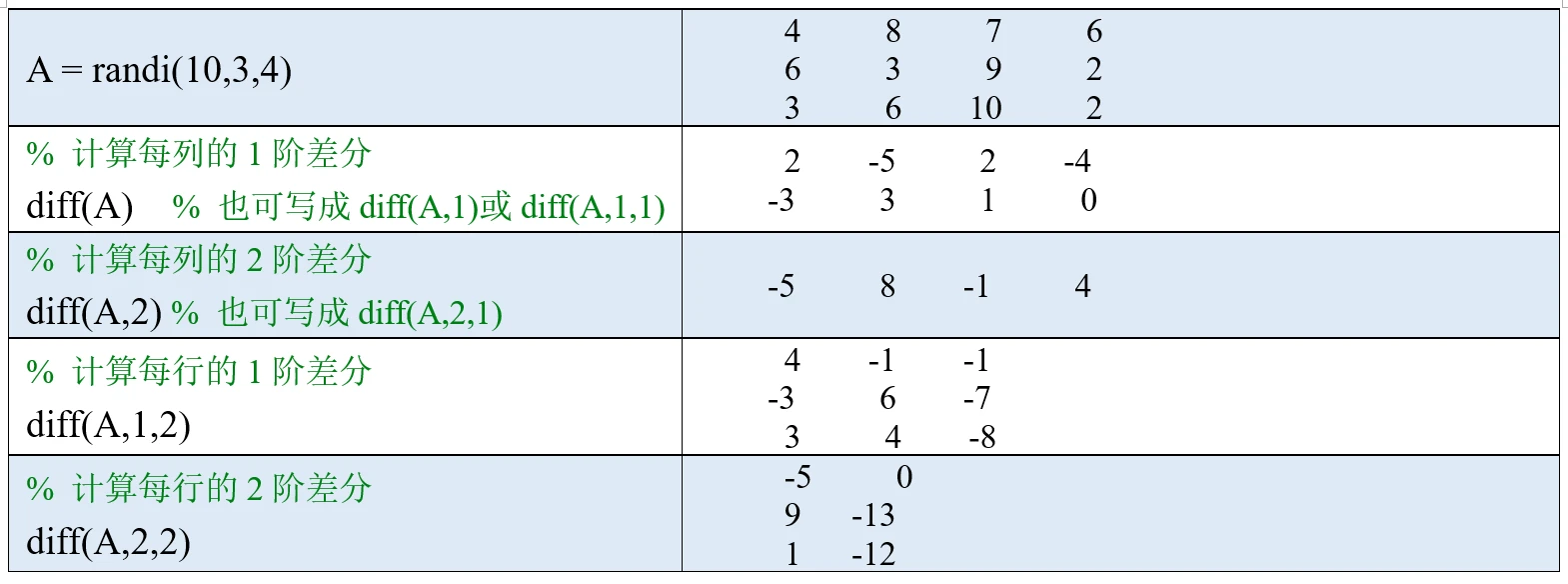
注意,diff函数不支持使用'omitnan'参数来忽略向量或者矩阵中的NaN值。
假设向量 ,即向量y有n个元素,那么它的平均值等于.
在MATLAB中,mean函数可以用来计算平均值,它的使用方法和sum函数类似。
(1)如果A是一个向量,则mean(A)可以计算向量A的平均值。

(2)如果A是一个矩阵,则mean(A,dim)可以计算A沿维度dim中所有元素的平均值。
类似的,dim=1时,mean(A,1)也可以简写成mean(A).
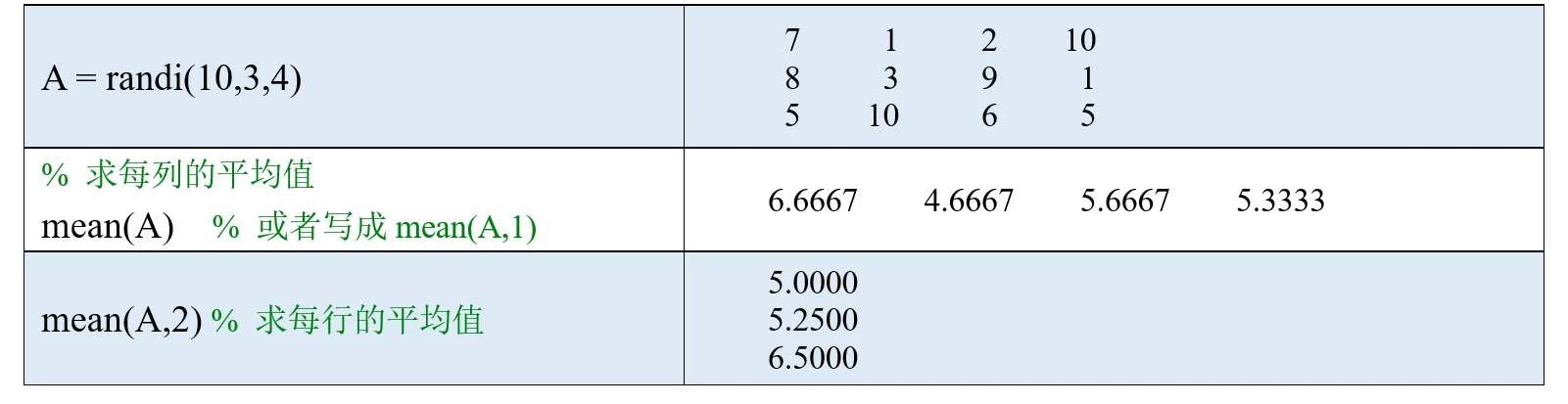
(3)也可以在最后加一个输入参数: 'omitnan', 这样计算时会忽略NaN值。
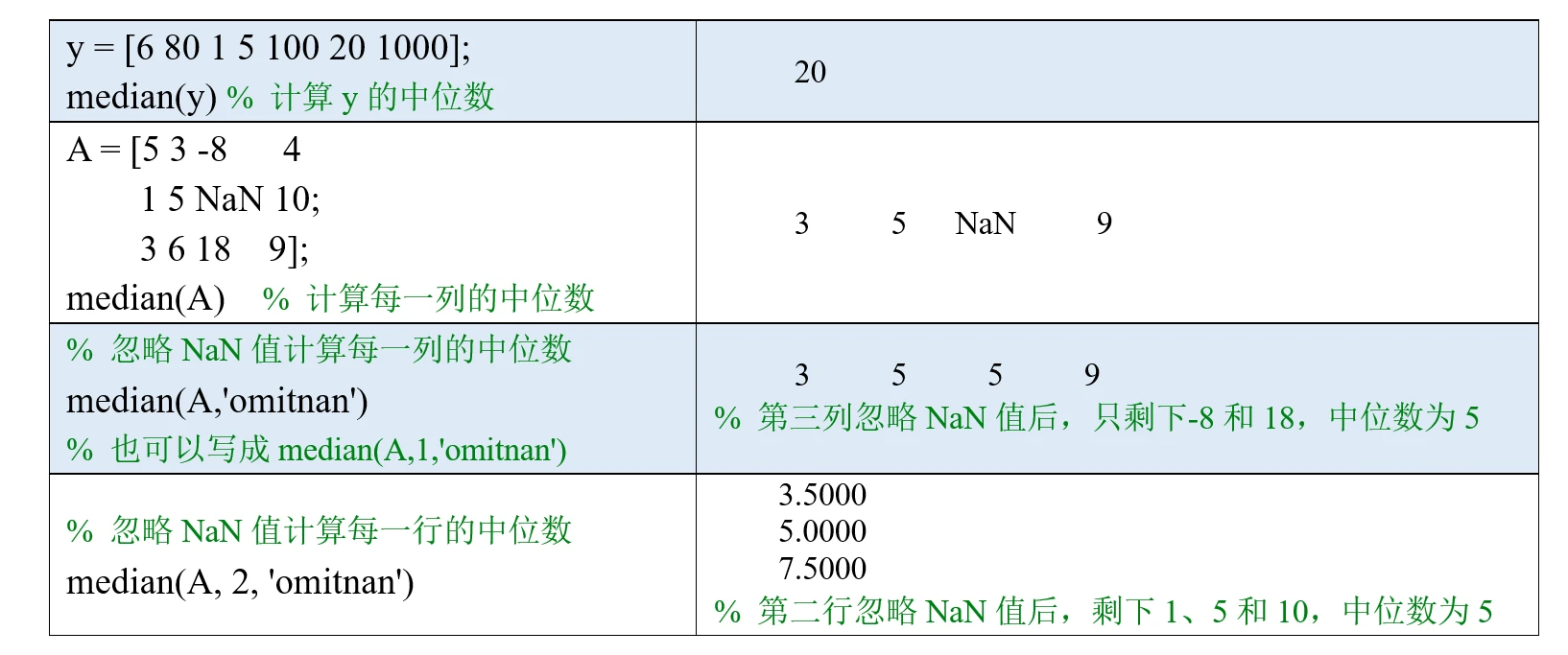
中位数又称中值,我们将数据按从小到大的顺序排列,在排列后的数据中居于中间位置的数就是中位数。
假设有一个向量, 向量y中有n个元素,我们先将向量y按照从小到大的顺序排序,得到新的向量
, 那么当n为奇数时,中位数为
; 当n为偶数时,中位数为
.
下面是手算中位数的步骤:

在MATLAB中,median函数可以用来计算中位数,它的使用方法和mean函数类似。
众数是指一组数据中出现次数最多的数。一组数据可以有多个众数,例如向量[1 3 -1 2 1 3]中,1和3都出现了两次,它们都是这组数据中的众数。
MATLAB中可以使用mode函数计算数据的众数,调用方法也和mean函数类似,但是mode函数可以有多个返回值。
以计算向量A的众数为例,直接调用mode(A)会返回A中出现次数最多的值。如果有多个值以相同的次数出现,mode函数将返回其中最小的值。

如果A是一个矩阵,则mode(A,1)或者mode(A)可以沿着行方向进行计算,得到每一列的众数;mode(A,2)可以沿着列方向进行计算,得到每一行的众数,这里的1和2表示维度dim。

注意:使用mode函数计算众数时会自动忽略NaN值,我们不能额外添加'omitnan'参数,否则会报错。

现在我们来看mode函数有两个返回值的例子,如果A是一个向量,[M,F] = mode(A)得到的M表示向量A的众数,F表示众数M在向量A中出现的次数。
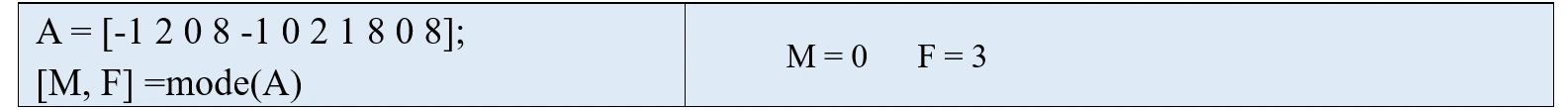
上面这个例子中,有两个众数,分别是0和8,它们出现的次数都是3次,此时MATLAB会返回最小的那个数作为众数。有同学会想,MATLAB能不能把这些众数都输出呢?
当然可以,我们需要用到mode函数的第三个返回值:[M,F,C] = mode(A), 这里的C是一个元胞数组,元胞数组里面有一个列向量,列向量中的每个元素都是向量A的众数。(注意,元胞数组是使用大括号{}括起来的,元胞数组(cell array)里面的元素可以包含不同的数据类型,例如标量、向量、矩阵、字符串等,后面章节中我们会专门讲解元胞数组的用法)
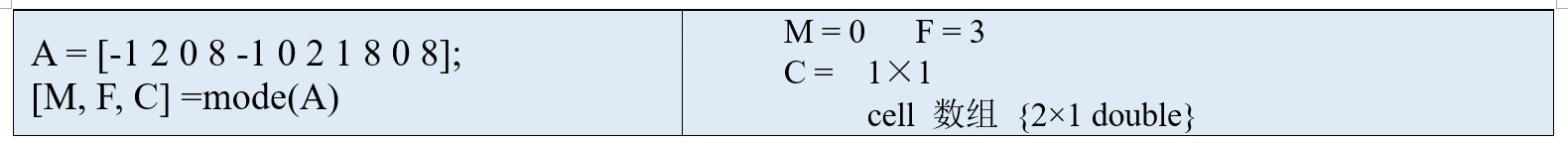
变量C就是元胞数组,它的大小为1×1,即一行一列,因此里面只有一个元素,这个元素是一个2行1列的列向量。我们可以使用大括号索引的方式来提取元胞数组中的元素:

命令C{1}可以提取出元胞数组C中的第一个元素:列向量[0; 8]。这个列向量中的元素0和8都是向量A的众数。
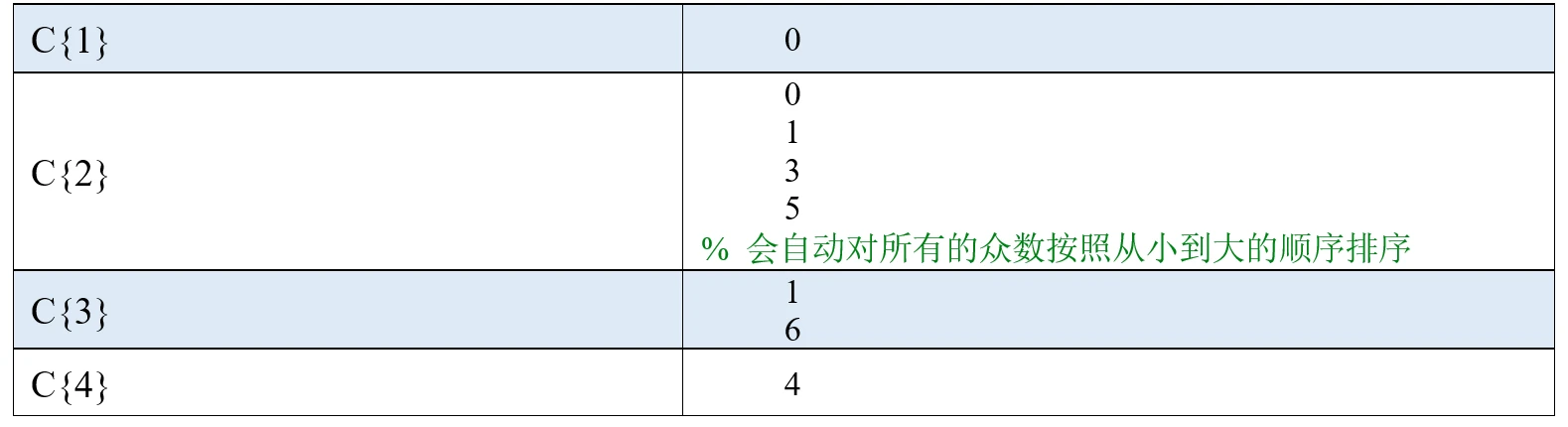
以上是A为向量时的情况,如果A是一个矩阵,mode函数也可以有两个返回值或三个返回值,后两个返回值代表的含义与A为向量时类似。我们直接看下面的例子:

M是一个包含四个元素的行向量,里面第k个元素表示第k列的众数,例如第1列的众数为0;如果有多个众数,那么会返回最小的那个值,因此第2列返回的众数为0。
F也是一个包含四个元素的行向量,它表示M中的各个众数在其所在列中出现的次数,例如第1列的众数0在第1列出现了2次。
C是一个大小为1×4的元胞数组,里面的第k个元素表示第k列的所有众数。从元胞数组C的结果来看,第一个和第四个元素分别为0和4,这说明第1列和第4列都只有一个众数,分别是0和4;C中第二个元素是一个4行1列的列向量,这说明第2列有四个众数;C中第三个元素是一个2行1列的列向量,这说明第3列有两个众数。
我们可以使用大括号索引提取C中的每个元素:
类似的,我们也可以计算A矩阵每一行的所有众数,结果如下:
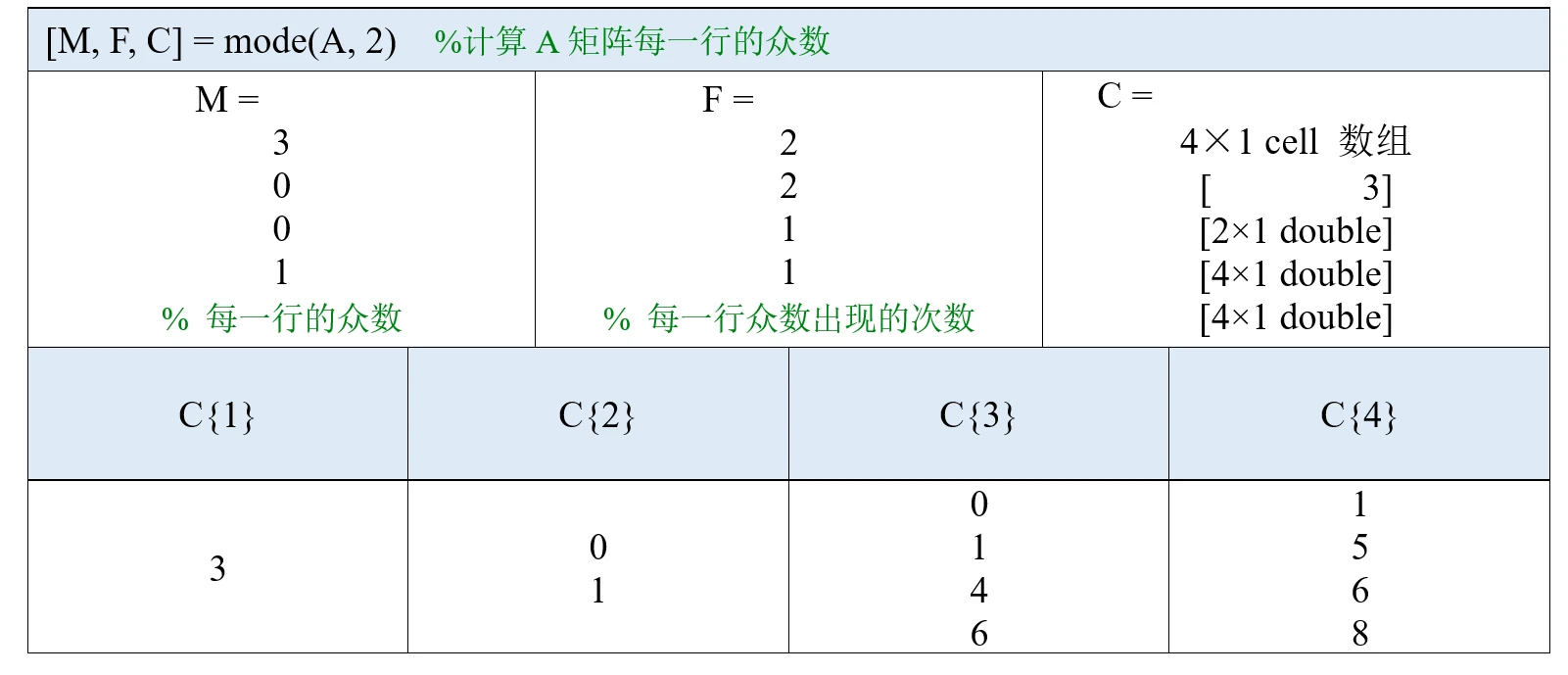
下面对mode函数做一个总结:
(1) mode函数可用来计算一个向量或者矩阵中的众数。如果mode函数只有一个返回值,那么它的用法和mean函数、median函数类似。
(2) 如果A是一个向量,那么M = mode(A)可以计算向量A的众数,若存在多个众数,则只会返回其中的最小值。
(3) 如果A是一个矩阵,那么M = mode(A, dim)可以计算矩阵A沿着维度dim中所有元素的众数。当dim=1时沿着行方向进行计算,即得到每列的众数;当dim=2时沿着列方向进行计算,即得到每行的众数。另外,mode(A,1)可以简写成mode(A)。
(4) mode函数不能使用'omitnan'参数,MATLAB在计算众数时会自动忽略向量或者矩阵中的NaN值。
(5) mode函数最多能有三个返回值:[M,F,C] = mode(A). 如果A是向量,那么M表示向量A的众数,F表示众数M在向量A中出现的次数,如果A中存在多个众数,MATLAB会返回最小的那个数作为M,第三个返回值C则是一个元胞数组,里面包含了A的所有众数。如果A是矩阵,那么M、F和C分别代表每一列的众数、每一列众数在所在列中出现的次数以及每一列的所有众数构成的元胞数组。
另外,本小节用到了元胞数组的知识,元胞数组中的元素用大括号{}括起来,各元素可以是不同的数据类型,要提取元胞数组中的元素可以使用大括号进行索引,例如,要提取元胞数组C中的第一个元素,可以使用C{1}。未来章节我们会系统学习元胞数组的用法,感兴趣的同学可以提前在MATLAB官网搜索关键词进行学习。
方差是概率论与数理统计里面的知识点,我们先简单回顾一下相关的内容。
先来看个例子:第一组数据是6、8、10、12、14;第二组数据是-10、0、10、20、30。显然两组数据的均值都是10,但第二组数据的离散程度更大一些。
方差就是用来描述这种离散程度的一个统计量,当两组数据的平均值相同时,方差较大的一组数据的离散程度更大。有一个常举的例子:一个射击队要从两名运动员中选拔一名参加比赛,选拔赛上两人各打了10发子弹,在得分均值相差不大的情况下,应选择方差更小的队员。
在现实生活中,我们收集到的数据可分为下面两类:
根据收集的数据类型的不同,我们计算方差的公式也有所区别。

从上方的计算公式可以看出,总体方差和样本方差在计算时的区别在于分母上是否要减1。
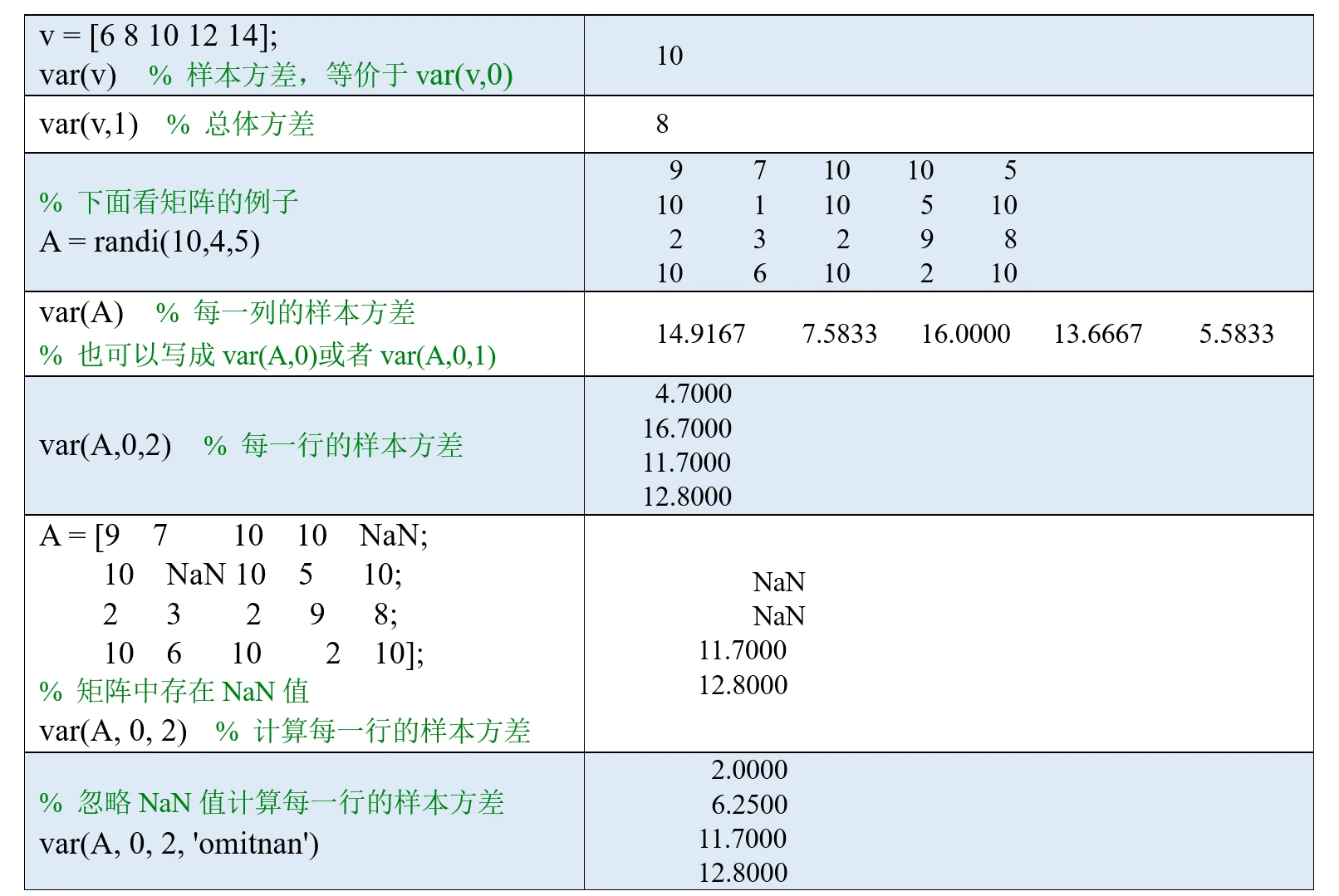
MATLAB中使用var函数计算方差:
(1)如果A是一个向量,那么var(A, w)可以计算A的方差,当w=0时,表示计算样本方差,w=1时表示计算总体方差,另外,var(A, 0)也可以直接简写为var(A)。
(2)如果A是一个矩阵,则var(A, w, dim)可以计算矩阵A沿维度dim上的方差。
当dim为1时,var(A, w, 1)可以简写为var(A,w);若w为0,则可以进一步简写为var(A),即默认情况下MATLAB会沿行方向计算得到每一列的样本方差。
(3) 如果数据中存在NaN值,可以在var函数的最后加上'omitnan'参数来忽略NaN.
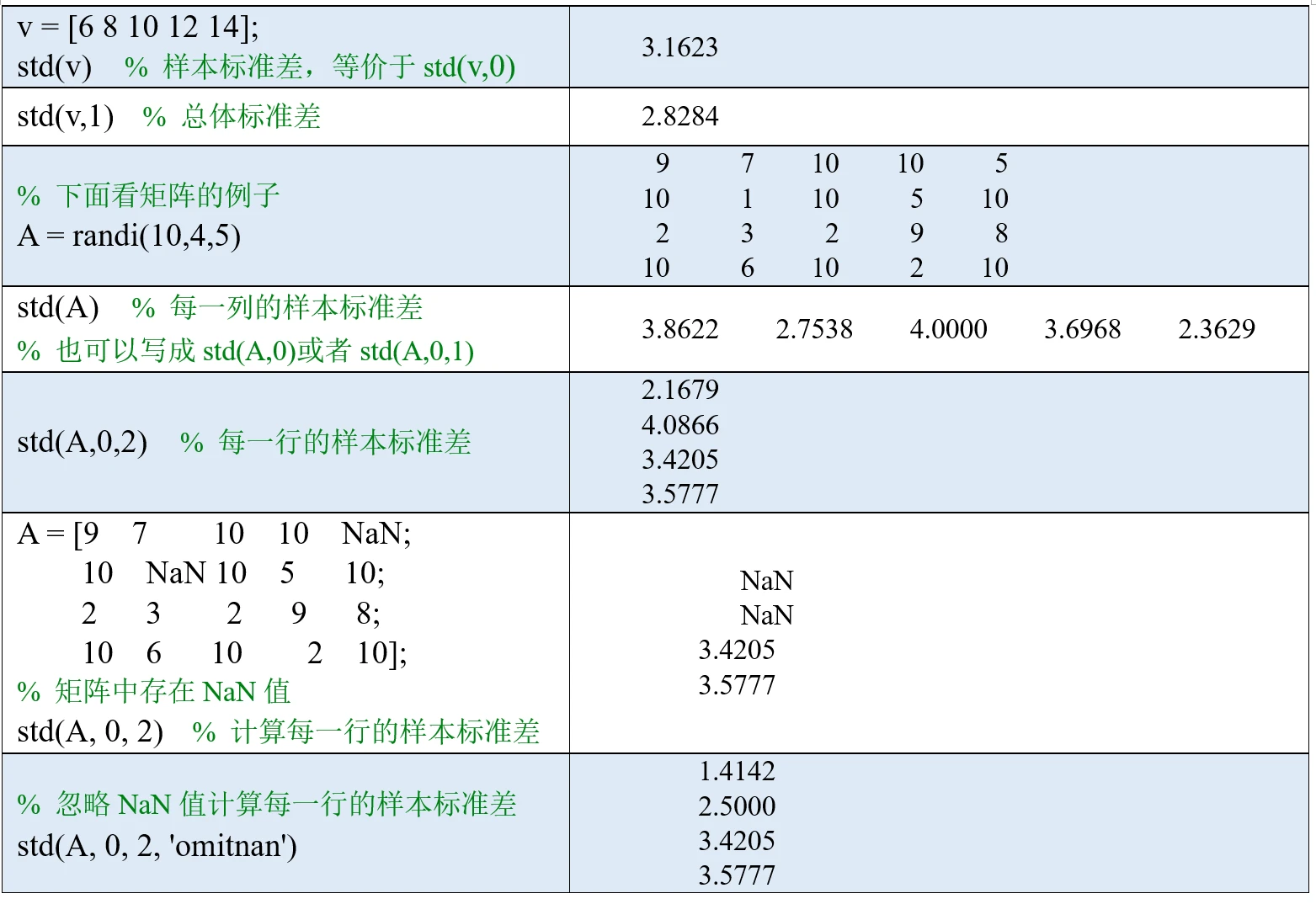
标准差是方差的算术平方根,它也是用来反应数据离散程度的一个统计量。那么问题来了,既然有了方差为什么还需要标准差呢?这是因为方差和数据原本的量纲(即单位)是不一致的,对方差的计算公式进行量纲分析容易看出,方差的量纲是原始数据量纲的平方,因此对方差开根号,得到的标准差的量纲和原始数据的量纲一致。
在MATLAB中,我们可以使用std函数计算样本标准差和总体标准差,它和var函数的使用方法完全相同。
min函数主要有两种用法:
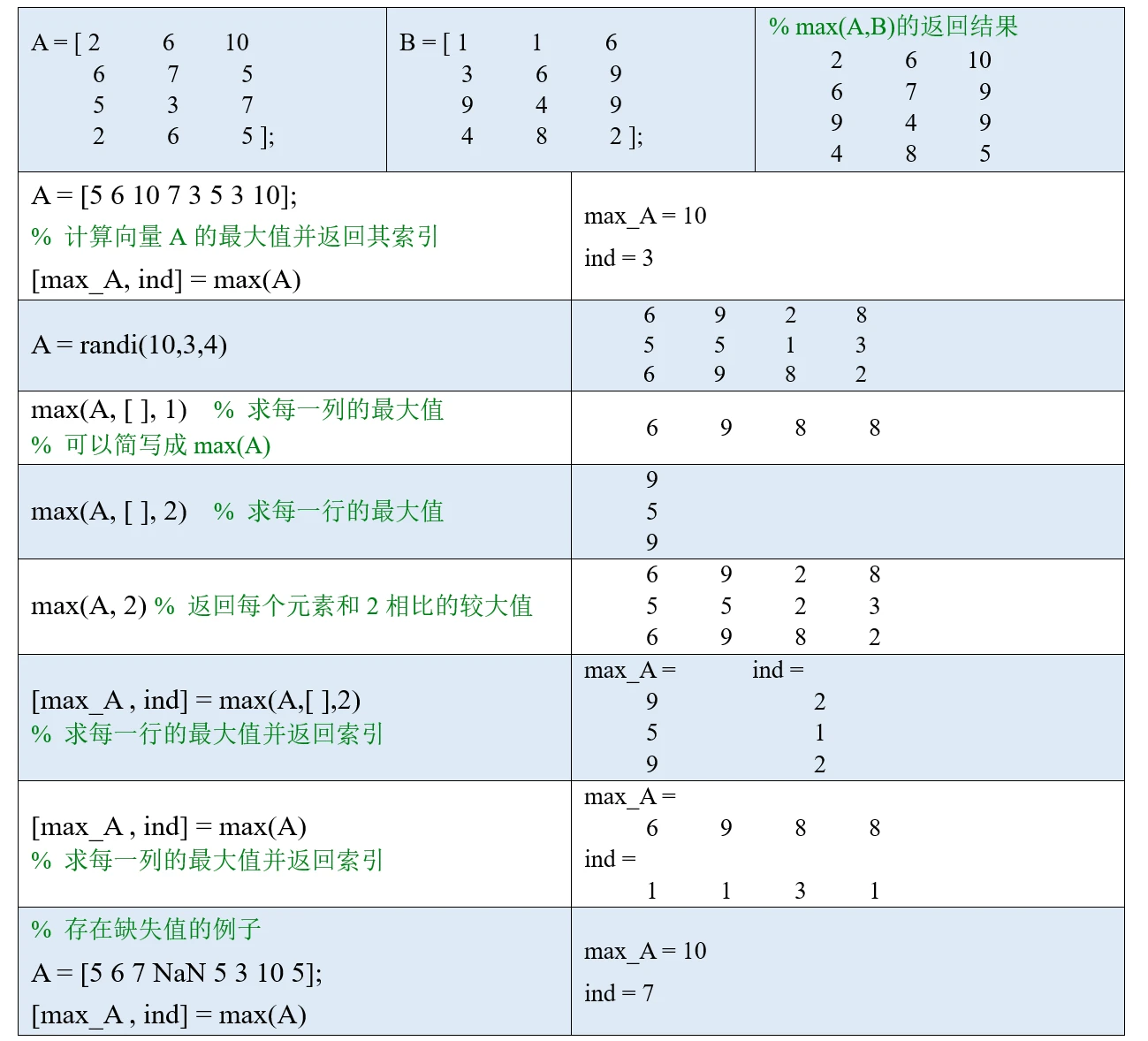
用法一:求两个矩阵对应位置元素的最小值: min(A,B)。

矩阵A和矩阵B的大小可以不一样,只要保证矩阵A和矩阵B具有兼容的大小就能够计算,MATLAB矩阵运算中支持的兼容模式会在“3.1.2算术运算”这一小节中详细介绍。
下面再举两个例子:表中第三列是运行min(A, B)后返回的结果。

用法二:求向量或者矩阵中的最小值,可以指定沿什么维度计算并返回索引。
具体用法有以下三种:
(1)如果A是向量,则min(A)返回A中的最小值。如果A中有复数,则比较的是复数的模长。

(2)如果A是矩阵,则min(A, [ ], 1)沿着A的行方向求每一列的最小值,也可以简写为min(A);min(A, [ ], 2)沿着A的列方向求每一行的最小值。这里的1和2表示矩阵的维度(dim)。
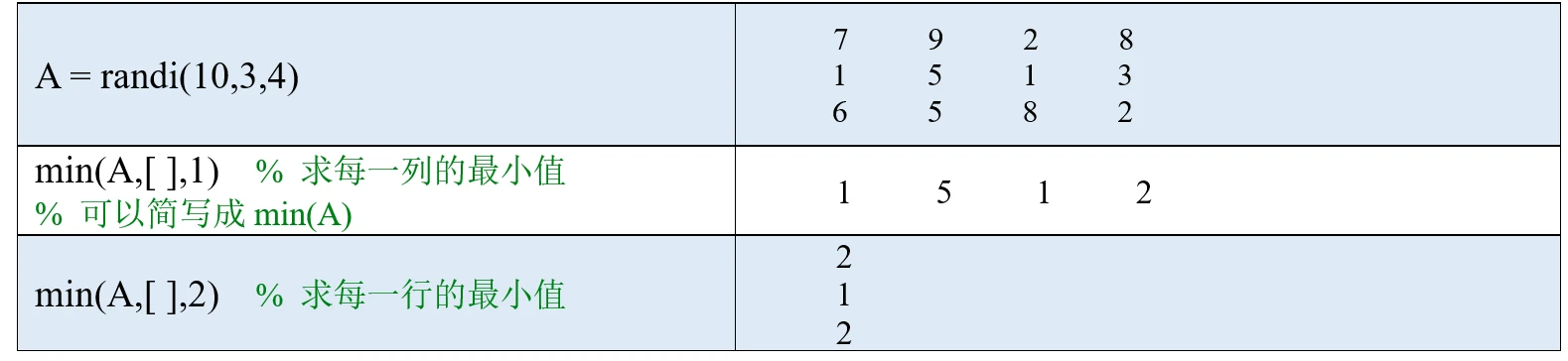
你可能会问: 为什么中间要加一个空向量[ ]? 如果不加的话,就是将A中每个元素和1或者2比较大小,并返回较小值。

(3)在求向量或矩阵的最小值时,min函数可以有两个返回值:[m, ind] = min(A). 第一个返回值m是我们要求的最小值,ind是最小值在所在维度上的索引。如果最小元素出现多次,则 ind是最小值第一次出现位置的索引。
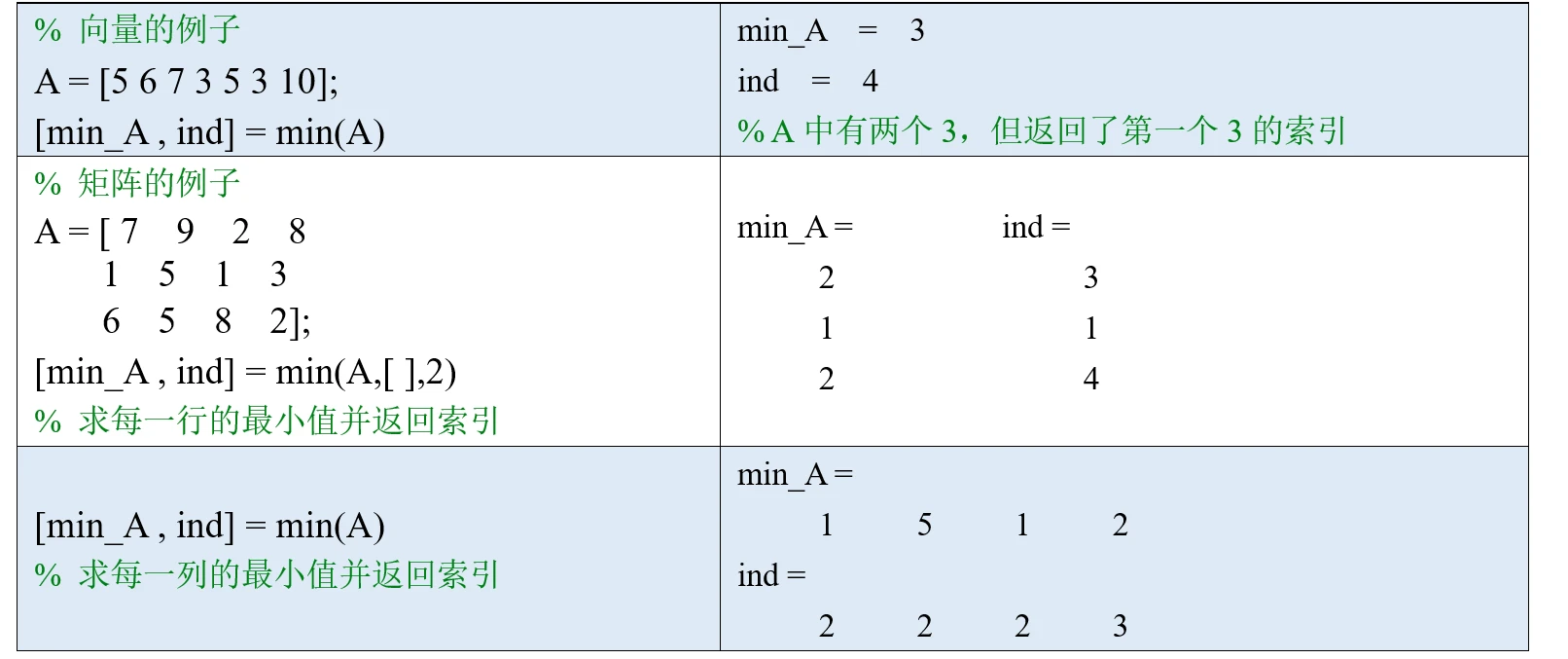
上面我们介绍了min函数的两种用法,如果向量或者矩阵中存在NaN值,min函数会自动忽略,大家不需要单独对NaN值进行处理。
max函数和min函数的用法完全相同,它是用来求最大值的函数,下面我们举几个例子。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删