根据笔者尝试,暂且得到的结论是:
1、模式匹配法需要注意积分限
2、模式匹配法的建模参考坐标不重要,重要的是最终矩阵形式,不同的形式影响着场解
(如果笔者的代码没有问题的话,从目前的实践来看,应该是这样的)
3、笔者尝试,采用归一化tan,并结合邓的矩阵形式对于求解TE波的截止频率很有效(在HFSS中找到了很多个相符的结果),对于求解TM波的很不敏感甚至无效(没找到一个和HFSS相符的结果),而不归一化,令系数部分的cos和sin分置于两侧,并结合贾的矩阵形式,则对于TM波的截止频率略有效(确实找到了一个与HFSS中的截止频率相近的结果)
笔者参考了三篇文献,邓素芬的硕士学位论文《机载》,贾瑶的硕士学位论文《模式》,张本全的博士学位论文《微波》,主要是基于前两篇文献,通过脊波导模型,学习模式匹配法
贾的矩阵形式和张的矩阵形式相近,且张的细节更少,所以张的就没有进一步看了。
邓的细节最多,笔者结合了赫兹位函数的一点概念,按部就班地复现了其关于TE波的数学内容,并且在matlab上实现了代码,且与HFSS仿真对照,确定了其关于TE波的内容是有效的
不过,笔者按邓的方法,推导TM波时,发现,matlab上的结果无效,基本对不上HFSS的结果
在第二次学习实践中,笔者学业上已经基本了解了位函数概念,并且花费更多时间去复现,并比对,邓和贾的推导及效果差别,通过采用邓和贾的方法分别对TE、TM波进行求解,共编成了四类代码,获取了本文开头的那三点结论。
笔者发现,这些论文有个操作,那就是积分外的如kn、sin(kn*x),cos(kn*x)等项放置在一起,虽然没有给出解释,但是翻阅外文文献,发现如出一辙。结合笔者的实践来看,笔者隐隐感觉,kxn的位置,与sin(kxn)等三角函数的位置,这里的相对位置关系,与最终结果是有联系的(当然,也可以这样解释,不同的矩阵形式必然有不同的kn与三角函数的相对位置关系,而不同的矩阵形式导向了不同的场解)
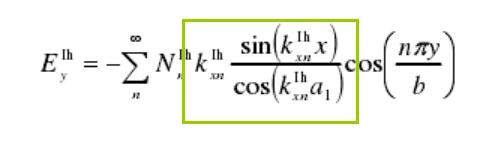
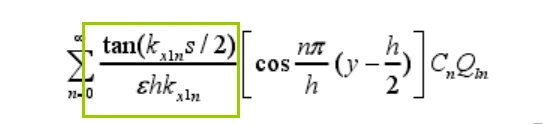
以上论述,与笔者实践完全相符,如果有误,则完全是笔者本人学业不精所致,欢迎在评论区指正,若使笔者因此而获益则感激不已。
对于希望学习模式匹配法的朋友,下面附上一则代码,希望有所助益。
a,b,s,h的定义与邓的论文中双脊波导的模型定义一致,笔者的HFSS建模也遵循此定义。
邓素芬论文中关于TE波的模式匹配法的相关代码:

下面为函数det_deng_TE
function out = det_deng_TE(a,b,s,h,N,M,fre)%邓素芬模型
%该函数用于求得det矩阵,a、b、s、h均为脊波导尺寸,N为模式数,M影响det矩阵元素值
% 先求出各部分子矩阵,然后采用矩阵运算的方式,得到det矩阵
c0=2.99792458e8;
kc=2*pi*fre/c0;
kn=eye(N+1);
km=eye(M+1);
k=eye(M+1);
% H1
H1=eye(N+1);
for n=1:(1+N)
kn(n,n)=sqrt((kc)^2-((n-1)*pi/h)^2);
if n==1
d=1;
else
d=0.5;
end
H1(n,n)=tan(kn(n,n)*s/2)/kn(n,n)*h*d;
end
% H2
syms y;
Ppm=ones((N+1),(M+1));
for p=1:(N+1)
tp=(p-1)/h*pi;
for m=1:(M+1)
tm=(m-1)/b*pi;
Ppm(p,m)=(-tm*sin(0.5*(b-h)*tm)+tm*cos(h*tp)*sin(0.5*(b+h)*tm)-tp*cos(0.5*(b+h)*tm)*sin(h*tp))/(tm^2-tp^2);
if (isnan(Ppm(p,m)))||(isinf(Ppm(p,m)))
f=cos(tp*(y-h/2))*cos(tm*(y-b/2));
Ppm(p,m)=int(f,y,[-h/2,h/2]);
end
end
end
for m=1:(M+1)
km(m,m)=sqrt((kc)^2-((m-1)*pi/b)^2);
if m==1
d=1;
else
d=0.5;
end
k(m,m)=cot(km(m,m)*(a-s)/2)/km(m,m)/b/d;
end
Plm=Ppm.';
H2=Ppm*k*Plm;
% H
H=H1-H2;
out=H;
end
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删