概念：

满足 “以任意节点为根的一颗子树左右高度差≤1” 这个条件的二叉树叫做平衡二叉树

AVL 插入操作:

在讲述插入操作之前，需要知道这几件事:

1. 因为在每次插入节点之后都会调整整颗树为平衡树,所以在插入节点之前一定是一棵平衡树
2. 平衡破坏时，只需要调整最小失衡子树即可
3. 最小失衡子树在插入节点之前高度差一定为1，因为新插入的节点才导致高度差变为>1
4. 在插入的过程中遇到的最后一个高度差为1的节点,以这个节点为根的子树的平衡状态可能会被破坏.
5. 从被破坏的位置向插入位置的路径中,所有子树高度差都为1,而且是由于插入新节点导致的,在插入之前这条路径上的所有子树高度差一定为0.(因为3)
6. 倒着看,从插入节点向上查找最小失衡子树的过程中,若遇到一个左右子树高度差为0的节点,那么整棵树仍是平衡状态(高度没变)

插入操作:

记录到最后一个左右子树高度差不为0的节点A，因为只有这棵子树才可能成为最小失衡子树。

判断左插还是右插.

1. 插入后仍然平衡，最后一个左右子树高度差不为0 的子树此时高度差变为0
2. 插入后不平衡，从插入位置往上到最后A路径上所有子树高度差此时变为1，(之前是0)
1. 往A左孩子的左子树插。左孩子的左右子树高度差之前是0，现在变成了1 (右旋操作)
2. 往A左孩子的右子树插。左孩子的左右子树高度差之前是0，现在变成了1.(先左旋，后右旋)
3. 往A右孩子的左子树插…..
4. 往A右孩子的右子树插….. (只有这四种情况.)

a. LL情况

由于A是最后一个高度差为1的节点，然后在A左孩子的左子树上插入，它只能是这种情况(未插入):

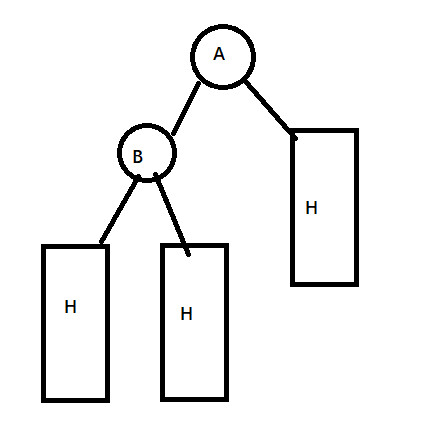
B的左右子树高度一定相同. (因为A是最后一个高度差为一的节点) ,在插入之后导致了这颗子树不平衡:

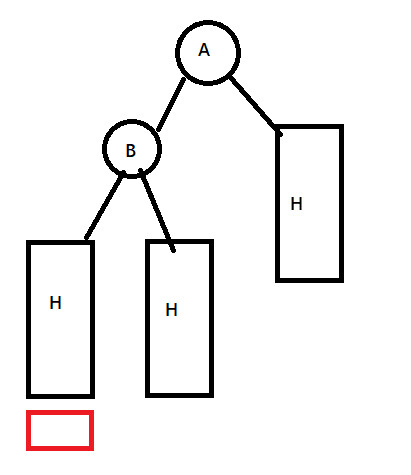
(其中两个红色任意一个都可以是新插入的节点)

一次右旋即可调整为平衡树：

注意观察，在插入之前这个子树的高度是H + 2，此时整颗树是平衡二叉树。

在插入并重新调整之后，这颗子树的高度仍然是H + 2，所以并不会影响整颗树的平衡状态，此时整棵树仍然是平衡二叉树。

b.LR情况

这个就是a情况中往b的右子树上插入，只不过这里我们还需要考虑一下B的右孩子的情况(插入之前):

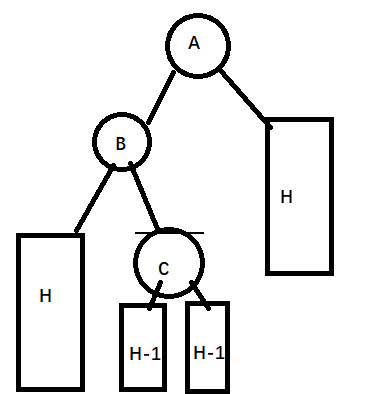
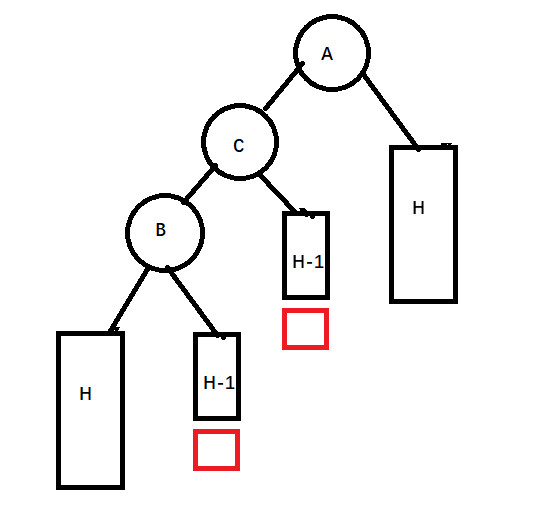
还是同样的原因，由于A是最后一个左右子树高度差为1的节点，所以B的左右子树高度相同，C的左右子树高度相同。在插入一个新的节点之后变成了这样:

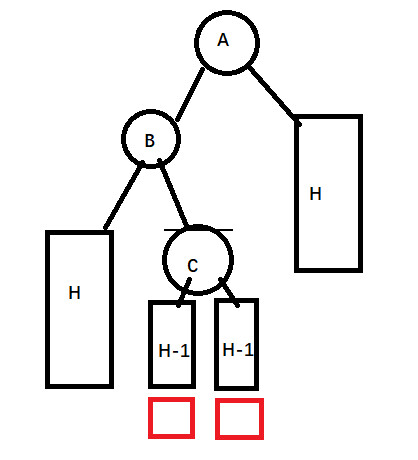
(图中新插入的节点为两个红色节点中的任意一个)。此时需要先左旋，转换为1 中的情况:

接着右旋：

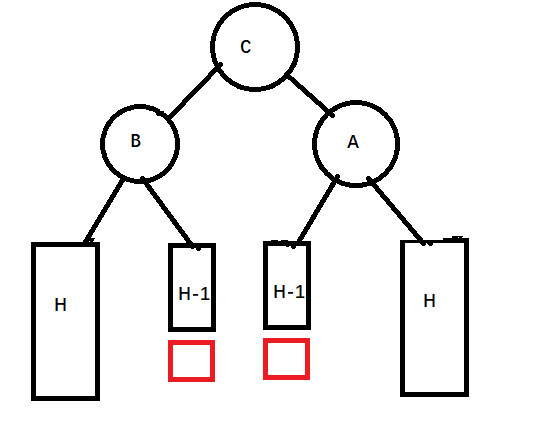
此时这颗子树就被调整为了平衡二叉树，且它的高度是H+2，与插入之前这颗子树的高度一样。所以在插入之前整棵树是平衡状态，在插入并且调整之后整棵树仍然是平衡状态。

RL与RR情况与上面两种情况类似，这里就不详细说明了。

为什么只需要调整最小失衡子树就行？

在a,与b两种情况中应该容易看出，我们调整的都是最小的那颗失去平衡的树。在插入之前与调整之后这颗子树的高度不变，不会影响整颗树的平衡状态。

删除操作:

如果要删除的节点不是叶子节点，我们找一个叶子节点与要删除的节点交换位置。

现在我们只需要考虑删除叶子节点即可。

删除叶子节点可能会导致某一棵子树平衡状态破坏，注意如果某棵子树的平衡状态破坏，那么调整之后，这颗子树的高度会减1，那么之后还可能会破坏其他子树的平衡状态。所以需要调整以 ”从叶子到根路径上所有节点为根“ 的子树的平衡状态。但是即使破坏了平衡状态，高度差最大不会超过2。

插入操作的一种实现方式：

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>

#define max(a,b) ((a)>(b) ? (a) : (b))

struct AVLTreeNode{
	int m_height;
	int m_val;
	AVLTreeNode*m_left;
	AVLTreeNode*m_right;
	AVLTreeNode*m_parent;
};

int GetTreeHeight(AVLTreeNode* node){
	if (node){
		return node->m_height;
	}
	return 0;
}

void LeftRotate(AVLTreeNode* node){
	assert(node);
	AVLTreeNode*parent = node->m_parent;
	parent->m_right = node->m_left;
	if (parent->m_right)
		parent->m_right->m_parent = parent;
	node->m_left = parent;
	node->m_parent = parent->m_parent;

	if (node->m_parent)
		if (node->m_parent->m_left == parent)
			node->m_parent->m_left = node;
		else
			node->m_parent->m_right = node;

	parent->m_parent = node;
	//
	parent->m_height = 1 + max(GetTreeHeight(parent->m_left), GetTreeHeight(parent->m_right));
	node->m_height = 1 + max(GetTreeHeight(node->m_left), GetTreeHeight(node->m_right));

	if (node->m_parent)
		node->m_parent->m_height = 1 + max(GetTreeHeight(node->m_parent->m_left), GetTreeHeight(node->m_parent->m_right));
}


void RightRotate(AVLTreeNode* node){
	assert(node);
	AVLTreeNode*parent = node->m_parent;
	parent->m_left = node->m_right;
	if (parent->m_left){
		parent->m_left->m_parent = parent;
	}

	node->m_right = parent;
	node->m_parent = parent->m_parent;
	if (node->m_parent)
		if (node->m_parent->m_left == parent)
			node->m_parent->m_left = node;
		else
			node->m_parent->m_right = node;


	parent->m_parent = node;

	//
	parent->m_height = 1 + max(GetTreeHeight(parent->m_left), GetTreeHeight(parent->m_right));
	node->m_height = 1 + max(GetTreeHeight(node->m_left), GetTreeHeight(node->m_right));

	if (node->m_parent)
		node->m_parent->m_height = 1 + max(GetTreeHeight(node->m_parent->m_left), GetTreeHeight(node->m_parent->m_right));
}


AVLTreeNode* insert(int val, AVLTreeNode*root){

	AVLTreeNode * NewNode = new AVLTreeNode;
	NewNode->m_height = 1;
	NewNode->m_val = val;
	NewNode->m_parent = 0;
	NewNode->m_left = 0;
	NewNode->m_right = 0;

	if (root == NULL){
		return NewNode;
	}
	//
	AVLTreeNode * subTree = NULL;				//可能的最小失衡子树.
	AVLTreeNode ** node = &root;
	AVLTreeNode * parent = NULL;

	while (*node){
		if (
			abs(GetTreeHeight((*node)->m_left) -
			GetTreeHeight((*node)->m_right)) == 1){
			subTree = *node;
		}
		parent = *node;
		if (val < (*node)->m_val){
			node = &(*node)->m_left;
		}
		else{
			node = &(*node)->m_right;
		}
	}
	//现在node 是要插入的位置.
	NewNode->m_parent = parent;
	*node = NewNode;

	//调整路径上的树高度.
	node = &NewNode->m_parent;
	while (*node && *node != subTree){
		(*node)->m_height = 1 + max(GetTreeHeight((*node)->m_left),
			GetTreeHeight((*node)->m_right));
		node = &(*node)->m_parent;
	}

	if (subTree){
		//平衡破坏.
		if (abs(GetTreeHeight(subTree->m_left) -
			GetTreeHeight(subTree->m_right)) == 2){

			if (val < subTree->m_val){
				if (val < subTree->m_left->m_val){
					if (subTree == root)
						root = subTree->m_left;

					RightRotate(subTree->m_left);			//LL.
				}
				else{
					LeftRotate(subTree->m_left->m_right);	//LR.

					if (subTree == root)
						root = subTree->m_left;
					RightRotate(subTree->m_left);
				}
			}
			else{
				if (val >= subTree->m_right->m_val){
					if (subTree == root)
						root = subTree->m_right;
					LeftRotate(subTree->m_right);			//RR
				}
				else{
					RightRotate(subTree->m_right->m_left);	//RL

					if (subTree == root)
						root = subTree->m_right;

					LeftRotate(subTree->m_right);
				}
			}
		}
	}
	return root;
}


int CheckGetTreeHeight(AVLTreeNode* root){
	if (!root)
		return 0;
	return 1 + max(CheckGetTreeHeight(root->m_left), CheckGetTreeHeight(root->m_right));
}

bool ValidAVL(AVLTreeNode* root){
	if (!root)
		return true;
	//检查子树是否为平衡二叉树.
	if (!ValidAVL(root->m_left))
		return false;
	if (!ValidAVL(root->m_right))
		return false;

	if (abs(CheckGetTreeHeight(root->m_left) - CheckGetTreeHeight(root->m_right)) > 1){
		return false;
	}
	return true;
}

int main(){
	AVLTreeNode* root = NULL;
	srand(time(0));
	for (int i = 0; i < 10000; i++){
		root = insert(rand(), root);
	}
	if (!ValidAVL(root)){
		printf("error ,Invalid AVL Tree");
	}
	else{
		printf("Valid AVL Tree");
	}
	return 0;
}

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删