背景：

地震的发生会破坏原有的自然平衡和社会稳定，易引起一系列二次破坏，这种破坏在空间上和时间上可能比地震本身更具危害性。其中，火灾是建筑物主要面临的地震次生灾害之一，虽然是局部的，但往往是毁灭性的。在多重灾害工况下，构件的承载力和反应规律会变得非常复杂和不利于掌控；对于已经受损的构件节点若继续承载其他次生灾害时，其破坏模式和失效机理是不可知的。

如何利用ANSYS来模拟建筑在震后次生火灾的情形呢？

震后次生火灾设计到多物理场耦合的问题，因为结构变形对温度场的影响较少，本案例以间接耦合为例进行分析，将温度场的结果传输到结构场进行模拟分析，具体流程如下：

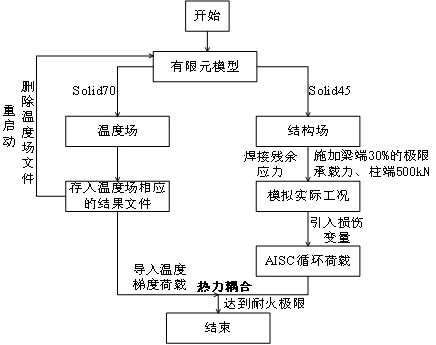
   图1 震后火计算流程简图
 

一、温度场设定

根据室内火灾升温曲线的特点，且假设燃烧空间的空气温度是分布均匀的，在此基础上对其火灾升温情况进行研究探讨，从而建立其室内火灾下标准的温度与时间关系曲线。我国现行标准采用的是以欧洲规范ISO834标准升温曲线来制定的相关规范标准。为此，本案例也采用相应的ISO834标准升温曲线来施加温度荷载。

   图2 ISO834升温曲线图
   

温度场边界的设定：

热对流：

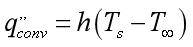
热辐射：

单位时间内表面极限发射功率：

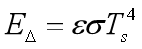
单位时间内表面极限接受功率：

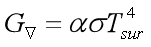
当表面吸收率等于发射率时（α=ε），则净辐射换热速率q为：

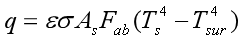
热传导：

二、结构场的设定

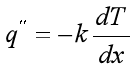
需设定热膨胀系数、热传导系数、比热容、密度等结构物理属性，还需设定弹性模量、屈服强度、泊松比、应力—应变关系曲线等结构力学性能参数值。

   图3 不同温度下钢材的应力与应变关系曲线
   

三、损伤指数D的选取

合理定义损伤指数D是评估地震造成结构损伤的可靠依据，基于对梁柱节点的耗能及变形考虑。本文采用较为广泛的Park-Ang模型，此模型充分的考虑到了其变形及试件耗能的影响。损伤指数D取值范围为0-1之间，0表示试件无损伤，1表示试件完全破坏或失效。其Park-Ang模型计算公式如下：

四、有限元模型的验证

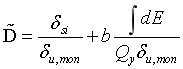
为了了解有限元模型在震后火灾下的有效性及精确度，需对有限元的结果与地震循环荷载试验及火灾下试验结果进行对比。

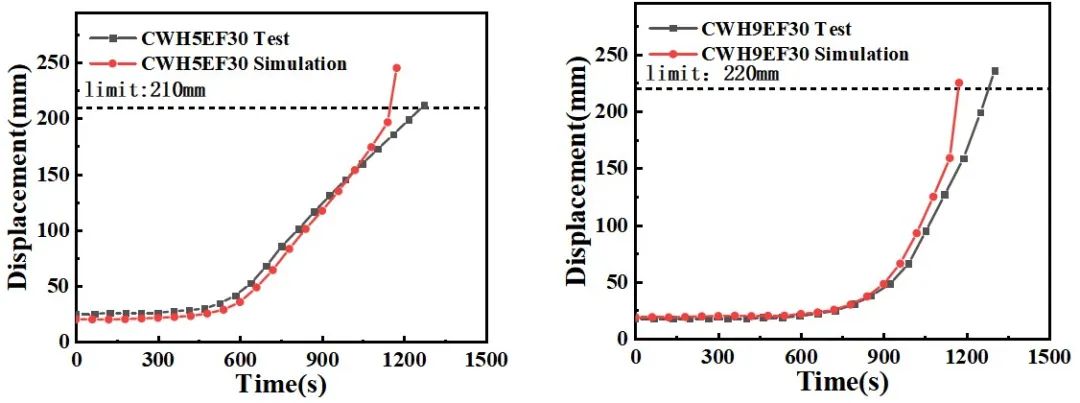
   图4 CWH5EF30和CWH9EF30升温时间与位移曲线对比验证图
   

   图5 破坏模式对比验证图
 

五、温度场结果分析

为了研究结构各区域的温度分布情况，提取了试件各个不同区域节点温度（900℃以内）随时间变化的曲线；分别提取了12组（1#到12#）时间—温度关系曲线与ISO384相对比。

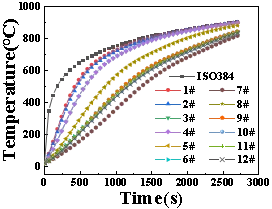
   图6 结构各测点时间—温度曲线图
 

为了了解试件在温度场中随时间变化温度分布的情况，可选取了500s、1000s、1500s和2000s时刻梯度温度分布的情况。

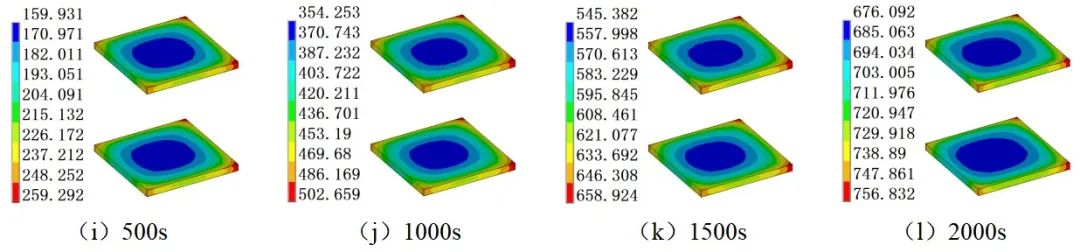
   图7 构件在不同时刻的温度分布图
   

六、地震损伤特征分析

合理的引入地震损伤是研究震后次生火灾关键的一步，本文对试件施加完模拟实际工况后，再次采用AISC规定的循环荷载加载。

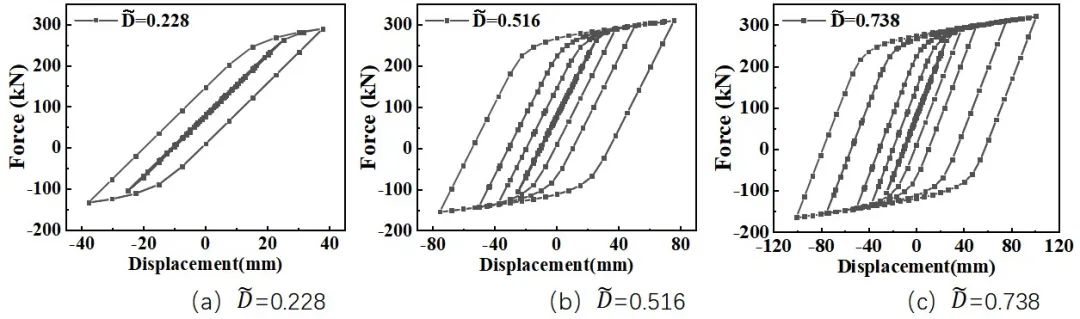
   图8 SPC3不同损伤指数下的滞回曲线
 

七、震后火失效模式特征分析

已在温度场中计算出此类构件节点各个部位温度随时间变化的温度梯度荷载，结构场中由地震引起的损伤大小。接下来所需做的工作是将两场数据进行无缝的对接，这是耦合场中至关重要的一步，节点与节点之间的数据正确无误交换将影响整个试件的失效模式。

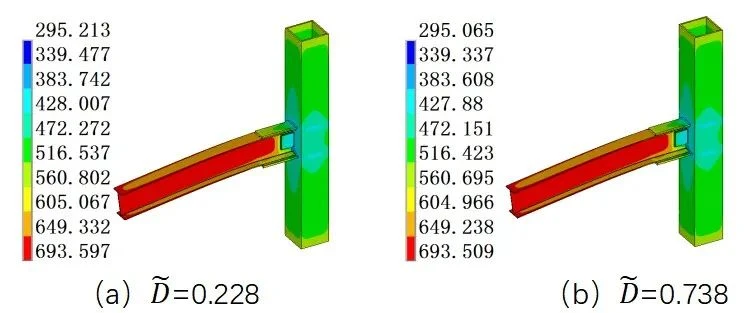
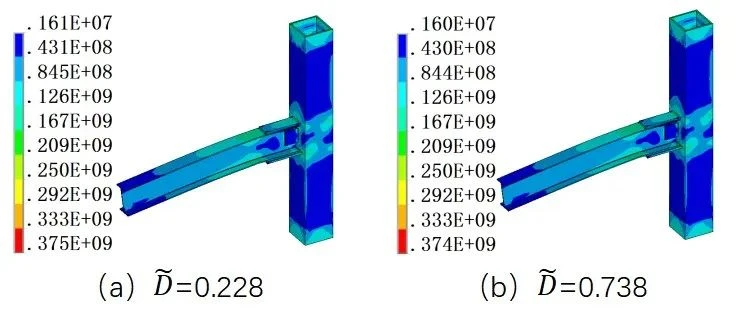
   图9 SPC3不同损伤指数下的失效应力云图
 

   图10 SPC3不同损伤指数下的失效应力云图
 

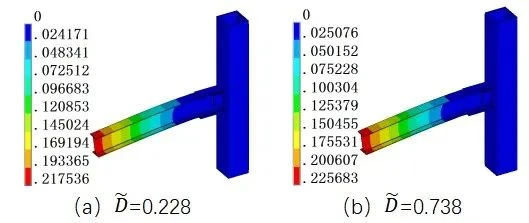
   图11 SPC3不同损伤指数下的失效位移图
 

综上所述，节点在不同损伤指数下其失效温度图与失效应力云图大致相同，对其失效位移图有一定的影响。可见，不同的地震损伤对其失效温度和应力图的影响较小，其主要是通过钢材的软化效应导致梁端位移过大或增长速率过大而破坏。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删