题记:
在中国,就数学软件使用者数目而言, Matlab 一直是占领着高地。这与 Matlab 优秀的数值计算和处理大数据的能力密不可分,还有一个关键原因就是中国用户多,交流环境良好。尺有所长,寸有所短,对于数学软件而言也是如此。比如就符号计算能力而言,Matlab显得相对不足,这时候恐怕要推荐一下 Maple或者 Mathematica。在使用软件的过程中,笔者发现很多人拿着一方的优势去有意贬低另外一个软件的不足,我认为大可不必,作为使用者不必拘泥,可以依据实际情况各取所需,为我所用。
本文就抛转引玉,介绍下maple软件通用的一些使用方法,以及使用Maple 求解旅行推销员相关问。Maple 是1982年加拿大Waterloo大学开发的一个符号运算和数值计算软件平台。之后几乎每年都进行发布新版本,目前最新的版本是2019年三月发布的Maple 2019。它在处理数学相关问题相当出色和专业。结合Maple软件学习数学也会增加相应的乐趣。
首先这里针对Maple初学者可能遇到疑惑的点解释一下:为什么有的命令输入可以起作用,有的命令明明输入了怎么也不起作用。
比如想画一个各占1/3的饼状图。我们查到命令: PieChart([1, 2, 3])。输入之,很不幸你将会看到原样输出。这是为什么?
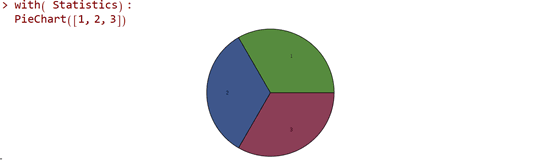
原因分析: Maple将一些专业性较强的关联紧密的函数命令集成到各种包里。如线性代数相关的 (典型的如求特征值,行列式) 就放到LinearAlgebra 包里,统计相关的就放在Statistics 包里。你使用内置命令之前需要查帮助文档(输入相关命令按F2)看看是不是在某个包里。上面说的函数PieChart 就在Statistics 包里。最直接的办法是添加with( Statistics): 效果图如下:
.gif)
言归正传,图是一类重要的数据结构,图论是研究图的一门学科。可以利用Maple进行图论的研究。当然也有的人用其绘制精美的图论里的图。注意:Maple 里的图不支持含重边和环边。
图论相关的放在GraphTheory 和 SpecialGraphs 包里,分别有197和 79 个函数命令。 还有一个是networks 包,不过这个包已经停止更新和维护,属于将被弃用的状态。Maple之所以保留并可以使用,估计Maple开发者有恋旧的美好情怀。
旅行推销员问题 (英语:travelling salesman problem, TSP)是这样一个问题:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。它是组合优化中的一个NP困难问题,在运筹学和理论计算机科学中非常重要。
一个判定问题(答案只有是或者否)属于NP 当且仅当这个问题是非确定型多项式时间可计算的。若NP问题类任何一个问题均可在多项式时间内转成问题A, 称 问题A 是NP 困难问题。说句人话就是这个问题本身比较复杂,随着问题规模越大,即使再强大的计算机也几乎无法求解。这时候规模大时候往往寻求近似解。
旅行推销员问题在图论中的一个等价形式是:给定一个加权完全图(顶点表示城市,边表示道路,权重就会是道路的成本或距离), 求一权值最小的哈密尔顿回路。
下面举一个现在看起来疯狂的例子。
大学毕业生小张准备骑自行车进行毕业旅行,出发地武汉,到南京,成都,合肥,西安,四个城市旅游,最后回到武汉。模型假设我们将五个城市视为图的5个定点,他们的直接距离是图的权重。上面城市分别记为1,2,3,4,5.
首先我们可以利用Wolfram Mathematica 联网功能一次性求出它们之间的距离。

.gif)
我们利用上面的距离数据在 Maple 里通过下列方式构建下面的图:
restart;
with(GraphTheory):
# 5个城市, 问题归结于在一个完全赋权图找一个最优Hamilton 圈.
distanceofcities:= Matrix(5, {(1, 2) = 459.149, (1, 3) = 977.647,
(1, 4) =319.501,(1,5)=649.843,(2,3)=1406.79,(2,4)=143.539,(2,5)=953.511,
(3,4)= 1264.16,(3,5)=604.452,(4,5)=827.082 }, fill = 0, shape = symmetric): # 定义赋权矩阵distanceofcities
travelcities:=Graph(distanceofcities): # 通过赋权矩阵构成的完全赋权无向图travelcities
DrawGraph(travelcities,stylesheet= [vertexborder = false, vertexpadding = 15,edgecolor="blue", vertexcolor="Gold",
edgethickness=5], font=["Courier",10], size=[400,400]);

然后利用内置命令求解:
t:=time[real]():
TravelingSalesman(travelcities);s
'time'=time[real]()-t; #记录运行时间
运行结果如下:
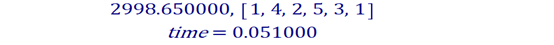
(*结果解读如下:选择路线为武汉->合肥->南京->西安->成都->武汉,总行程2998.65公里。运行时间是0.051秒。*)
如果此时我们将城市扩大到10个,并考虑有时候由于地理条件的诸多原因两地往返的路选择未必一样。也就是往返选择的路的距离未必一致,这时侯考虑的就是有向图了。Maple 照样可以处理。
n:=10:
A1:= Matrix(n, (i,j)->`if`(i=j,0,n*(n-i)^4+2*j+(n-i)^2+j^3));
# A1 赋权矩阵
G1:=Graph(A1):
t:=time[real]():
TravelingSalesman(G1);
'time'=time[real]()-t;
运行结果是
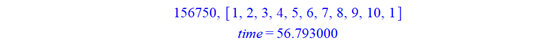
这时我们会发现内置命令为56.79300 秒,时间已经算多的了,有人会问我们有希望自己编写的代码比内置命令更节省时间吗?很多情况的确是可以幸运地做到的。下面的方面是把每个路线方法(共 10!/2= 1814400 种)进行比较。从方法上感觉很笨。
n:=10:
P:=Iterator:-Permute([seq(2..n)]):
cmin:=infinity: ord:= <"none">:
for v in P do
f:=add(A1[v[k],v[k+1]],k=1..n-2) + A1[1,v[1]]+A1[v[n-1],1];
if f<cmin then cmin:=f; ord:=copy(v) fi;
od:
cmin;tour:=[1, entries(ord,'nolist',indexorder),1];
'time'=time[real]()-t;
HighlightTrail(G1, tour, red);
DrawGraph(G1, style = circle);
运行结果如下:
.gif)

得到了相同的结果,但是令人惊讶的是时间却是1.775秒,远远小于内置方法。 其中原因估计有二:第一我们没有采用真正意义上的暴力计算,而是巧妙地采用所谓惰性计算方法-迭代,这里主要体现在:
P:=Iterator:-Permute([seq(2..n)]): 。
第二点,我们考察 Maple 里TravelingSalesman 函数帮助文档用的什么算法,可以看到如下文字: The algorithm is a branch-and-bound algorithm using the Reduce bound (see Kreher and Stinson, 1999).
于是我们知道主要采用分支定界算法,这个方法有时候搞不好枝搞地很多,将会花费很多时间去剪枝,有时候反而不如直接比较的方法来的快。所以说我们也不能过度依赖内置函数去处理问题,而是依据实际情况进行合理的处理。
至于较大规模的旅行销售员问题的近似计算,有兴趣地找找相关文献读读。
最后,如果大家有matlab/maple/mathematica相关算法问题,可以通过我们的微信公众号联系我们。
微信公众号:320科技工作室。




