这是专栏更新的第六天，加油陌生人！ 

        概览

    AVL树其实是在二叉搜索树上演变而来。所以在此我们简短地对二叉搜索树的相关概念进行一个简短地回顾。      对于二叉搜索树我们有如下的定义：

• 任意一个节点的值都大于其左子树所有节点的值

• 任意一个节点的值都小于其右子树所有节点的值

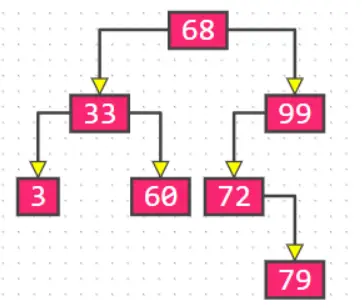
二叉搜索树示例

平衡二叉树所面临的问题：

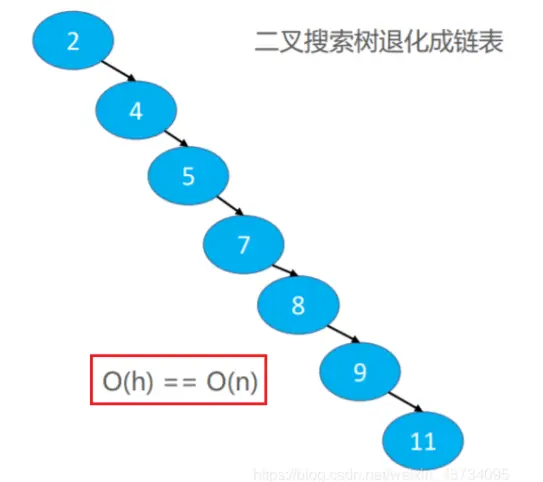
    二叉搜索树最大的特点就是他在最优情况系可以实现 O（）复杂度内完成信息的查询操作，但是最坏情况下他可能会面临如下的情况：

    如果给定的数据信息以：2,4,5,7,8,9,11的形式给出，此时便树便退化成单链表的形式，使得查询效率降低，所以就需要有一种机制来尽量避免树退化成单链表，所以AVL被提出。

    AVL树在原有的二叉搜索树的基础上增添一个新的限制：即每个节点的左右子树高度差绝对值不超过1。

    当高度差超过1时，我们就需要进行旋转操作，以此来避免搜索树退化为单链表的形式。一般来看导致失衡的情况主要有LL,LR,RR,RL等几种情况。

旋转操作

        对于AVL树考纲并没要求掌握具体的代码实现，能根据给定的数据信息构建出AVL树或者将不满足条件的搜索树进行进行旋转调整使其满足AVL树定义及可应对大部分考试。     但文章最后会给出旋转代码java版本的具体实现，仅做参考，不是考试重点。如果有兴趣的话可以尝试pat甲级的1066 ：Root of AVL Tree。     当然这都属于提升了，掌握了基本旋转技巧其实应对考试已经完全是足够的了。 

        在分析调整之前我们首先要区分清楚一个概念：我们常说的RR和LL说的是树失衡时的情况，而非旋转情况。

    很多人容易将失衡情况和旋转情况搞混，以为当发生LL不平衡现象时进行左旋转，这是错误的观点。

    文末会对整体的旋转情况进行总结回顾，以加深你对AVL树旋转的记忆。

LL 情况

    当我们在一个节点的左子树的左子树上插入一个新节点使得树发生失衡。此种情况称为LL。我们需要进行右旋转就能使其平衡。

        当LL情况发生时我们要通过右旋转来使得搜索树重新达到平衡。这个反转的过程具体如下：

    通过图我们很容易就可以看出对于LL失衡条件下的右旋调整情况主要有如下几个关键步骤：

        1.将失衡节点的左指针指向当前节点左子树的右子树节点 。

            如图所示：当前失衡节点为A，此时调整时首先将其左指针指向B节点的右子树信息

        2. 将当前失衡节点的左子树提升为父节点，失衡节点作为其右子树节点。

            如图所示：A的左子树B提升为父节点，调整A作为B的右子树节点信息。

RR情况

       当我们在一个节点的右子树的右子树上插入一个新节点使得树发生失衡。此种情况称为LL。我们需要进行左旋转就能使其平衡。

RR情况的旋转

RR时左旋操作

    调整过程：

        1.将失衡节点的右指针指向当前节点右子树的左子树节点 。

            如图所示：当前失衡节点为A，此时调整时首先将其→指针指向B节点的左子树信息

        2. 将当前失衡节点的右子树提升为父节点，失衡节点作为其左子树节点。

            如图所示：A的右子树B提升为父节点，调整A作为B的左子树节点信息。

    经过上述分析后我们明白了左旋 和右旋的具体操作细节，这是处理 LR,RL情况时所必须的技巧。

LR情况

       当我们在一个节点左子树的右子树上插入节点而使得失衡时，我们称这种情况为LR失衡。

    这种情况下我们需要旋转两次，首先经过一个右旋，然后经过一个左旋。

LR情况下的旋转

RL情况

       当我们在一个节点右子树的左子树上插入节点而使得失衡时，我们称这种情况为RL失衡。

          这种情况下我们需要旋转两次，首先经过一个左旋，然后经过一个右旋。

示例代码：（非重点）

  我，毅航同学。一名山大的普通计算机研究生，业余读读书，总结技术学习上的感悟。希能帮助到你。欢迎你同我一起进步，一起交流。