工作效率研究：男女搭配的科学依据

【案例】男女搭配干活不累-男女搭配工作效率研究

 问 题 背 景

许多人在异性面前会非常愉快地完成那些在同性面前极不情愿完成的任务，有时还表现得十分机智、勇敢，而许多上司也乐意让男女同事成为搭档，共同完成一个项目。这种现象心理学上又称为“异性效应”，即所谓“男女搭配干活不累”。那么这种说法到底靠不靠谱呢？我们一起来研究一下。

某科学管理研究机构想要测定男女搭配工作同个人单独工作相比工作效率的变化情况，于是在某机械加工厂内进行如下试验：随机分别抽取了10名男工和10名女工参与试验，首先记录下他们在一定时间内加工零部件的个数，接下来记录下他们在两两搭配工作后在同一时间段内加工零部件的个数。分析比较搭配工作前与工作后工人的工作效率有无明显差异。

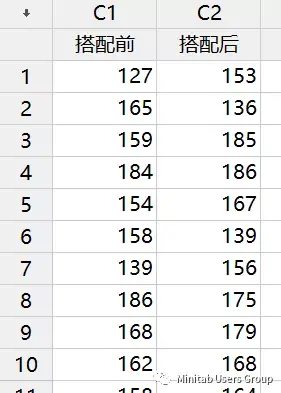
样本比较-描述性统计

统计分为两大类：描述性统计和推断性统计，描述性统计针对的对象是样本，推断性统计分析的对象则是总体。进行统计分析，我们更感兴趣的是总体的信息，但比较遗憾的是，总体的信息我们又很难得到，所以我们通过样本来推断总体，这就是推断性统计，而其中我们最常用的就是假设检验。

在对总体进行推断之前，对样本做一些描述性分析将有利于我们了解总体情况。

基于当前搭配前后的抽样数据，计算相应描述性统计量。

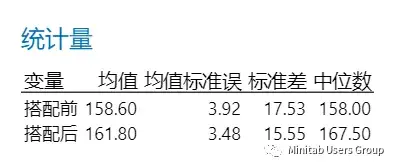
通过计算，我们发现搭配前后工人制造产品个数的平均值是不同的，搭配前是158.6，搭配后是161.8，男女搭配后略有提高。但抽样是有随机性的，不能直接由当前样本得到统计显著性结论，我们接下来还需要做假设检验。

检验前准备

要想执行严格的假设检验，往往想要满足一些前提条件：正态性、等方差等，我们先来验证一下这些前提条件。

01正态性

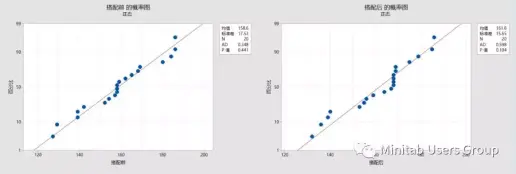
02等方差

配 对 T 检 验

由于该试验是对同一工人在搭配工作前后的工作效率进行对比分析，我们可以使用配对t检验。

您可以按照六个基本步骤正确地设置和执行假设检验。

01指定假设

基于前面的描述性统计分析，我们了解到配前后工人制造产品个数的平均值是不同的，搭配前是158.6，搭配后是161.8，男女搭配后略有提高。所以，这里我们的原假设和备择假设可以写成：

● H0: μ1-μ2=0（男女搭配无明显变化）

● H1: μ1-μ2＜0（男女搭配工作效率提高）

02选择显著性水平（又称为alpha 或 α）

最常用的显著性水平α=0.05。

03确定检验的功效和样本数量

通过计算功效和样本数量来确定需要收集多少数据，才能以较高的概率检测到与目标值之间存在需要的差值（略）。

04收集数据（见前面工作表）

05将检验的 p 值与显著性水平进行比较

在执行假设检验之后，将获得的 p 值与显著性水平α（通常为0.05）比较。

P＞α，不拒绝原假设

P＜α，拒绝原假设

06 确定是否定原假设还是无法否定原假设

配对T检验软件操作

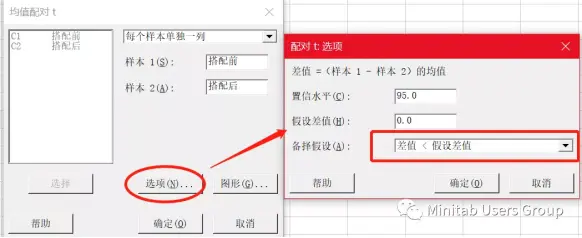
结果解释

配对T检验的结果显示，P=0.179，大于0.05，故不拒绝原假设，所以我们得到的结论是：对于该加工厂的工作，男女搭配的工作效率无明显差异。