1.什么是试验设计
1.1 试验设计的定义 在相当多的可能影响y的自变量中确定哪些自变量x 确实显著地影响着y,怎样去改变这些自变量x或如何设置这些自变量x的取值将会使y达到最佳值。这时,我们可以使用的最主要的手段和工具就是计划安排一批试验,并严格按计划在设定的条件下进行这些试验,获得新数据,然后对之进行分析,获得我们所需要的信息,从而找到改进的途径。这一整套步骤就组成了试验设计。 试验设计是这样一门科学,它是研究如何以最有效的方式安排试验,通过对试验结果的分析以获取最大信息。
1.2 试验设计的作用 (1)宏观上 六西格玛管理通常包含DMAIC五个阶段,主要用于改进现有过程。 界定:明确问题或流程输出Y及其测量,确定Y的标准 测量:测量系统分析、过程能力分析 分析:假设检验、单因子方差分析、多变异分析、相关及回归分析 改进:试验设计、看板、目视管理、5S管理等 控制:改进成果文件化、实施持续的过程测量与控制 (2)微观上 确定影响质量特性的关键因素及其水平 1.3 基本术语
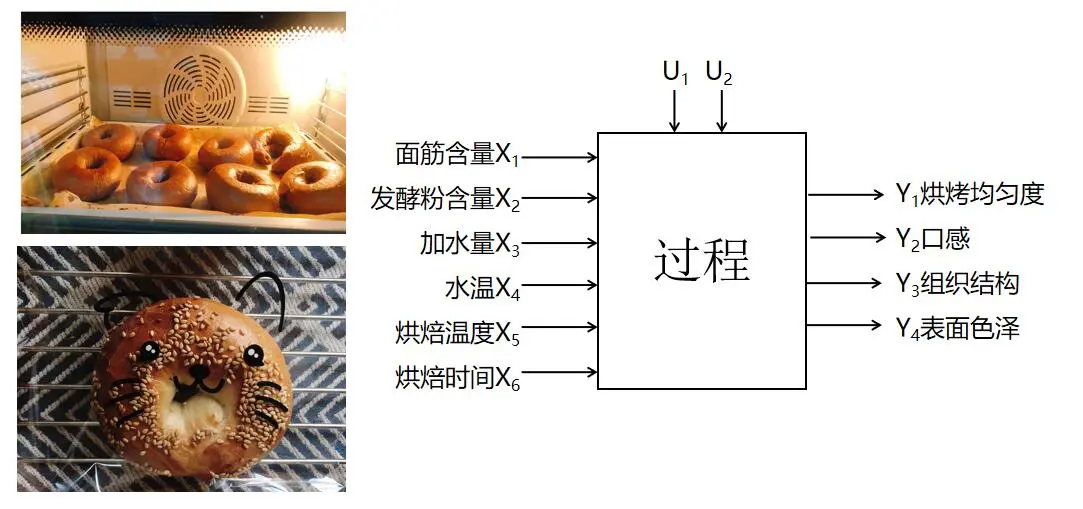
试验过程简图
(1)因子与响应变量 我们将影响响应变量的那些变量称为试验问题中的“因子”。 我们关心的输出变量,这些常被称为“响应变量”或“指标”。 (2)水平及处理 为了研究因子对响应的影响,需要用到因子的两个或更多个不同的取值,这些取值称为因子的“水平”或“设置”。 (3)模型与误差 考虑到影响响应变量y的可控因子是x1,x2, …,xk。
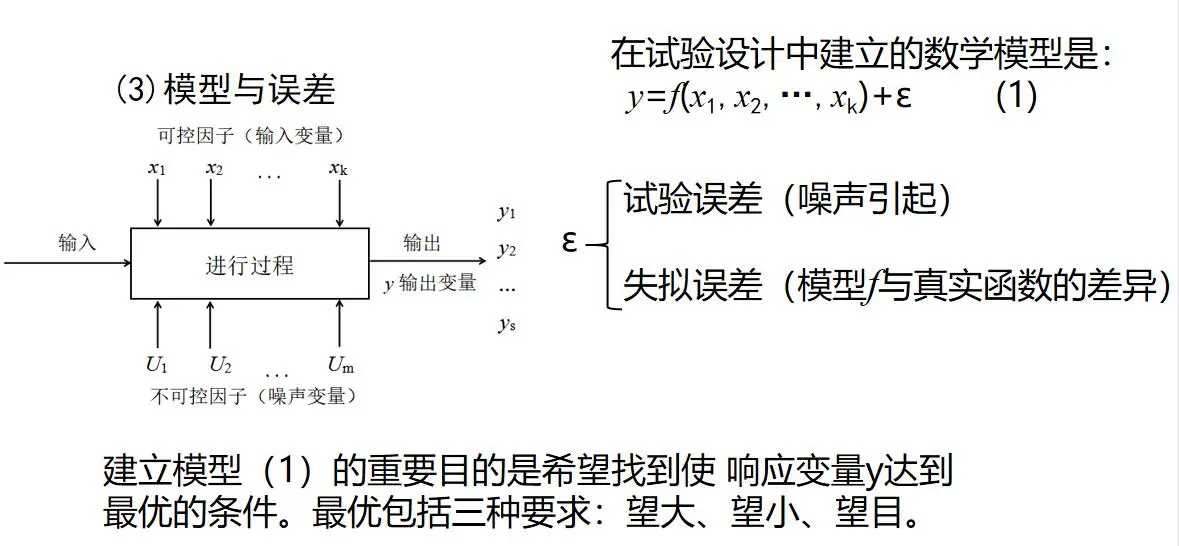
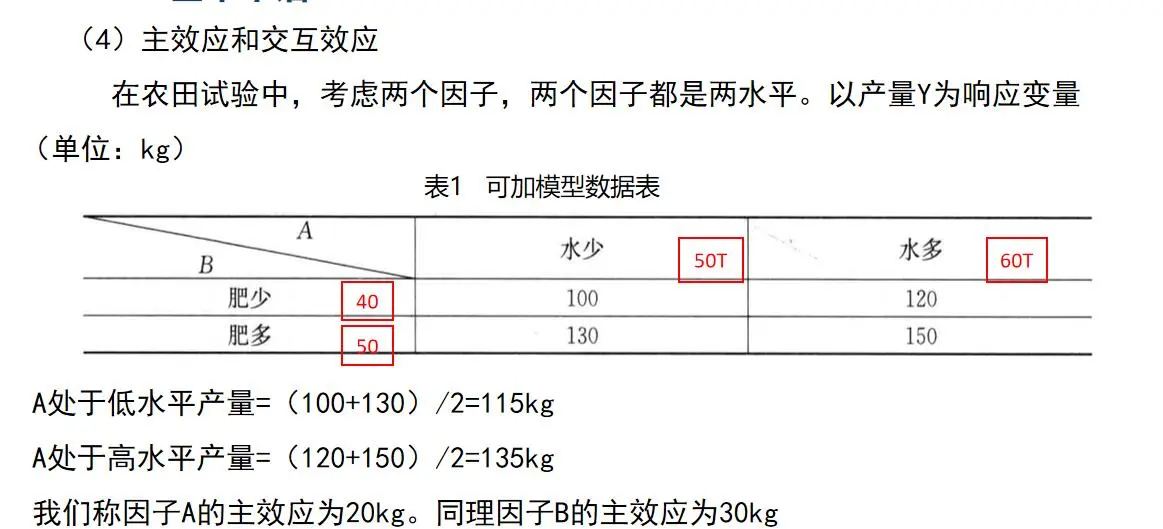

表2 可加模型数据表
A处于低水平产量=(100+130)/2=115kg A处于高水平产量=(120+170)/2=145kg 我们称因子A的主效应为30kg。同理因子B的主效应为40kg 定义两因子间的交互作用为:如果因子A的效应 依赖于因子B所处的水平时,则称A与B之间有交互作用 定义交互效应为下式: AB交互效应=[(170-130)—(120-100)]/2=10kg 有时一个因子主效 应很小,但只要某个含它的交互效应显著, 则这个因子就是重要的,就得予以保留 2 为什么做试验设计 世界最著名的发明家爱迪生一生艰苦奋斗,经历了无数次的失败之后,为人类发明了许多重要科技产品。他的座右铭是“天才靠的是百分之一的灵感和百分之九十九的汗水”。他的助手特勒撒( Nicola Telsa)于爱迪生去世后第二天在1931年10月19日的《纽约时报》发表纪念评论写道:”如果在爱迪生工作的黑屋中能有一支蜡烛照亮他前进的方向的话,以他蜜蜂般的勤奋,他将会获得远比他已发明的东西多得多的成果”。“我非常同情地观察到他的工作状况,但凡有一点点理论和计算能帮助他的话,将节省他百分之九十的精力”。 爱迪生是靠苦干拼出来的,他是在边试验边分析后确定下次试验该怎么做的。这种方法速度太慢,而且只能从已经得到的偶然出现的好结果出发,摸索着前进,无法预测何处将有更好的结果。这种凭直观猜测的方法已无法适应当代需求。 另一种在多因子试验中,常用的方法是单因子变化。 多个因子中,每个因子依次改变,而其他因子则保持在固定或选定的水平上。这样做肯定能比全面搭配所需要的试验次数少。 缺点:无法估计某些交互作用;对初始值敏感,会错过最优因子设置 全部因子全部水平进行搭配都进行至少一次试验的安排方法称为全因子试验。 缺点:试验次数多 8因子2水平:28=256 38=6561

3 试验设计的分类 3.1、根据试验的因子的个数,可以分为单因子、多因子。 3.2、根据试验的目的,可以分为因子筛选设计、回归设计、稳健性设计。 我们进行试验有两个基本目的:一是明确哪些自变量 x显著地影响着y;二是找出y与x间的关系式,从而进一步找出自变量x取什么值时将会使y达到最佳 值。“因子筛选设计”。由于这种试验的目的是针对因子的,因此这种试验设计属于“因子设计”,或称“析因设计”或“因析设计”。 因子设计和回归设计间确有相通之处:它们都 要建立回归方程。但因子设计只要线性的,而这里的回归设计指的是二阶的(通过RSM)。 3.3 试验设计的基本原则 有三个基本原则在试验设计中必须要考虑:完全重复(replication)、随机化 (randomization)和区组化(blocking)。 完全重复是指一个处理要施于多个试验单元。完全重复有时也简称为“复制”、“仿 行”等。一定要进行不同单元的 完全重复(replicate),而不能仅进行同单元的重 复取样(repetition)。 当然,完全重 复不一定要对所有处理全都重复,下面会介绍一些 方法来节省试验次数,例如可以安排只在“中心 点”处进行完全重复,别处只进行一次试验,这将大大节省试验费用。 随机化是试验设计的第二个原则。随机化的含义是以完全随机的方式安排各次试验的顺序和/或所用试验单元。 目的是防止那些试验者未知的但可能会对响应变量产生某种系统的影响。 随机化并没有减少试验误差本身,但随机化可 以使不可控因素对试验结果的影响随机地分布于各 次试验中,因此可以防止未知的但可能会对响应变 量产生某种系统影响的出现 区组化是试验设计的第三个原则。在实际工作中,各试验单元间难免会有某些差异,如果能按某种方式把它们分成组,每组内可以保证差异较小, 即它们具有同质齐性(homogeneous),而允许区组间有较大差异,这将使我们可以在很大程度上消除由于较大试验误差所带来的分析上的不利影响。 将全部试验单元划分为若干区组的方法称为区组化(blocking)或分区组。 例如,假定在白班、夜班时段内差异不大,而白班、夜班差异可能较大,就把白 班、夜班当作两个区组。这时在分析中就可以去除 掉白班、夜班间差异的影响,或尽可能把试验全都 安排在白班(或夜班)进行 4 试验设计的流程 粗略地说,试验设计包含计划、实施及分析三 个阶段。 1.计划阶段 这里又可以分为下面几个步骤: (1)阐述目标。究竟是为了筛选因子还是为 了找寻关系式?最终要达到什么要求? (2)选择响应变量。在一个试验中若有多种响应,则要选择起关键作用的且最好是连续型指标 作为响应变量。 (3)选择因子及水平。用流程图及因果图先列出所有可能对响应变量有影响的因子清单,然后 根据数据和各方面的知识及专业经验,也可以借助些工具,比如FMEA等进行细致分析并作初步的筛 选。(“宁多毋 漏”) (4)选择试验计划。根据试验目的,选择正确的试验类型,确定区组状况、试验次数,并按随机化原则安排好试验顺序及试验单元的分配,排好计划矩阵。 2.实施阶段 严格按计划矩阵的安排进行试验,除了记录响应变量的数据,还要详细记录试验过程的所有状 况,包括环境(气温、室温、湿度、电压等)、材 料、操作员等。试验中的任何非正常数据也应予以 记录,以便后来分析时使用。 3.分析阶段 分析中应包括拟合选定模型、残差诊断、评估模型的适用性并设法改进模型等。当模型最终选定后,要对此模型所给出的结果做必要的分析、解释 及推断,从而获得重要因子的最佳设置及响应变量的预测。当认定结果已经基本达到目标后,给出验 证试验的预测值,并做验证试验。 “全因子试验设计”(full factorial design) 的定义是:所有因子的所有水平的所有组合都至少 要进行一次试验的设计。 当因子水平超过2时,由于试验次数随因子个 数的增长而呈指数速度增长,因而通常只做2水平的全因子试验。但通常认为,加上了中心点之后的2水平试验 设计在工程实践中已经足够,在相当大程度上它可 以代替3水平的试验,而且分析简明易行,现已被工程师普遍使用。 1)将k个因子的2水平的全因子试验记为:2k试验。 实施的时机 大约是:先用部分实施的因子设计进行因子的筛选,让因子个数最后不超过5个,然后用全因子试验设计进行因子效应和交互效应的全面分析。进一步筛选因子直到因子个数 不超过3个时,则最后可以用响应曲面方法 (RSM)确定回归关系并求出最优设置。 2)代码化及计算 所谓代码化 (coding),就是将该因子所取的低水平设定的代 码(code)值取为-1,高水平设定的代码值取为 1,中心水平定为0。 好处:1、代码化后的回归方程中,自变量及交互 作用项的各系数可以直接比较,系数绝对值大者之 效应比系数绝对值小者之效应更重要、更显著 2、代码化后的回归方程内各项系数的估计量间是不相关的 3、在自变量代码化后,回归方程中的常数项(或称“截距”)就有了具体的物理意义。截距值是全部试验结果的 平均值,也是全部试验范围中心点上的预测值。 全因子试验分析 分析的第一要点是分析评估回归的显著性 关于ANOVA表的分析。这里包含三点:(1)看ANOVA表中的总效果。 H0:模型无效 H1:模型有效 无效:1)试验误差太大。 2)试验设计中漏掉了重要因子。 3)有可能是模型本身有毛病,例如模型有失 拟(lack of fit),或数据本身有较强的弯曲性 (2)看ANOVA表中的失拟现象。H0:无失拟 H1:有失拟 失拟:说明模型漏掉了重要的项(例 如高阶交互作用项等),应该补上 (3)看ANOVA表中的弯曲项。 H0:无弯曲 H1:有弯曲 本项计算的依据是:最初是以重复试验间的差异及失拟项的误差作为试验误差的估计,将高低水平的2个数据连同中心点的试验数据,构成自变量的3个不同的观测值,扣除线性项后可得二次项的平方和,将二次项误差的均方和与试验误差的均方和相比较,经过F检验即可判明是否呈现弯曲。 分析的第二要点是分析评估回归的总效果 (1)两个确定系数R2及R2adj 拟合的总效果可以用确定系数R2(也称为多元全相关系数 )及调整的确定系数R2adj(也称为调整的多元全相关系数。 (2)对于S值或S2的分析 平均离差平方和(adj MS)的数值则恰好是σ2的无偏估计量, 我们将其记为均方误MSE(mean square of error),而此量与其平方根S一并输出,可以认为 S值是σ的估计。 (3)对于预测结果的整体估计 我们特别要警惕得到的方程是受个别点影响而形成 的“虚假”回归方程。这种方程从表面上看,可能 拟合得还不错,但用作预测则效果并不好。为了鉴别回归方程究竟是不是虚假的,引入R-Sq(预测)。 分析的第三要点是分析评估各项效应的显著性 要注意的是:如果一个高阶项是显著的,则此高阶项所包含的低阶项也必须包含在模型 中。例如,二阶交互作用BC项显著,则B及C这两 个主效应项也一定要包含在模型中,即使表面上看 这两个主效应项本身并不显著。