产品
在讲解第三章课后习题的过程中，我给大家拓展了一些讲义中没有介绍的新函数，本文将对这些新函数进行总结，方便大家学习。
第三章课后习题的讲解视频：
下面表格中列举了这些函数的名称和功能，上方的讲解视频中也有介绍这些函数的使用方法，大家可以找到对应题目的讲解视频进行学习。另外，表中最后一列给出了各个函数的重要性，大家需要重点掌握重要性大于等于四颗星的函数，它们在后续的章节中可能会频繁使用；重要性小于等于三颗星的函数大家了解即可，它们用的频率不高。
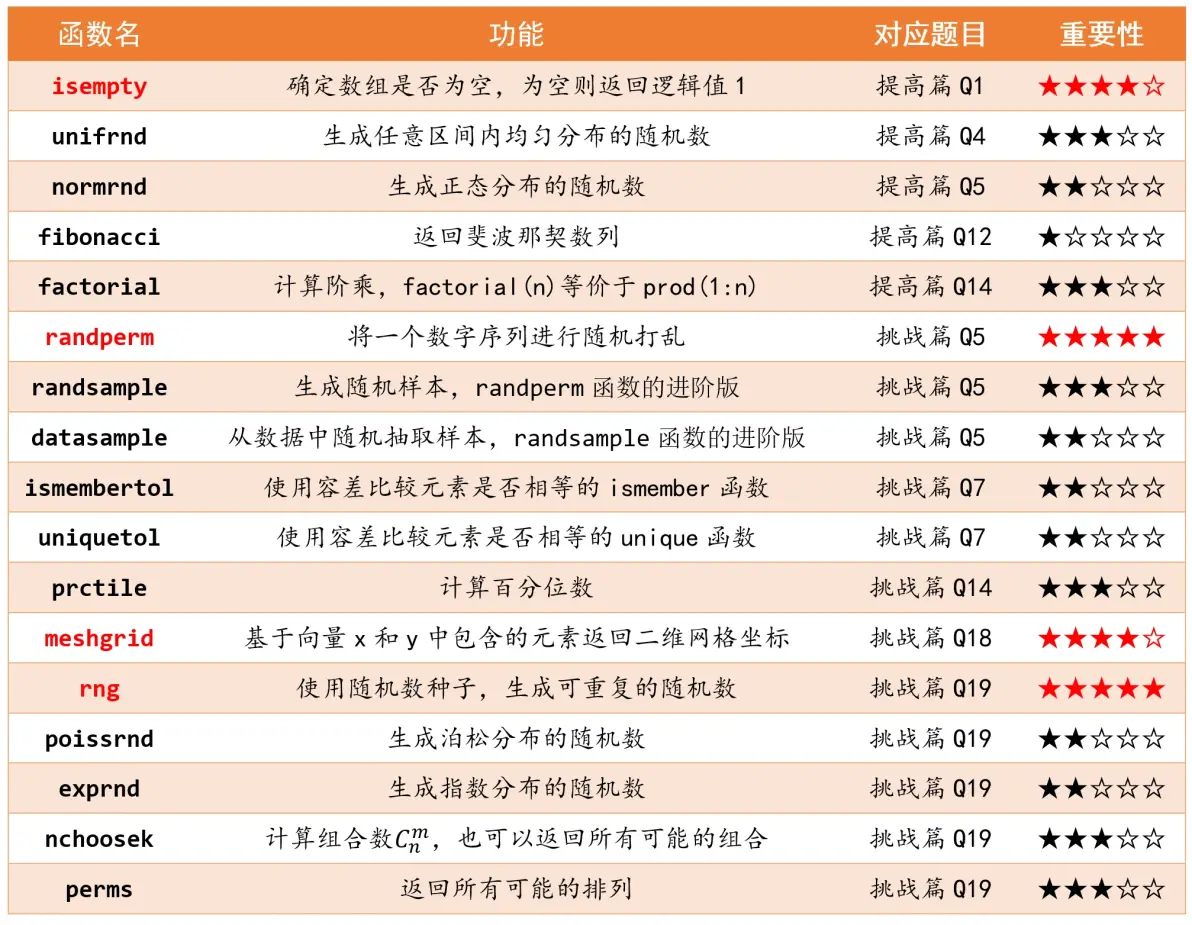
（1）isempty函数（★★★★☆）
如果 A 为空数组 [ ]， isempty(A) 返回逻辑值 1 (true)，否则返回逻辑值 0 (false)。
下面举个例子：假设我们想判断常数x是否是数组A中的某个元素，如果是则返回逻辑值1，不是则返回逻辑值0。我们可以使用下面两种方法：
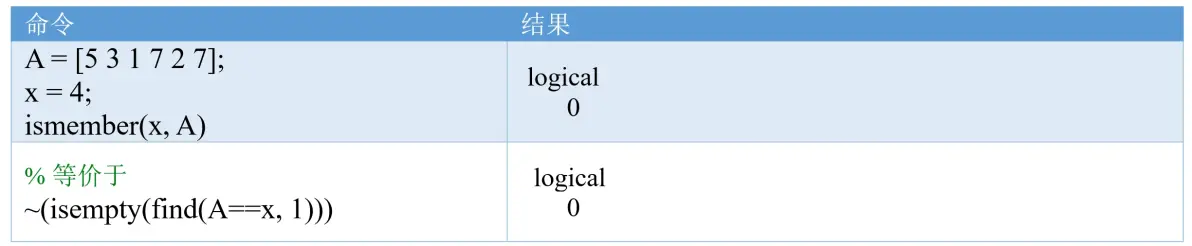
解释：find函数可以查找非零元素的索引，如果数组中所有的元素均为0，那么find函数返回空向量[ ]。因为A中所有的元素和x都不相等，所以A==x返回一个元素全为逻辑值0的逻辑向量，此时find(A==x, 1)返回空向量[ ]，因此isempty(find(A==x, 1))会返回逻辑值1，我们对这个结果进行逻辑非~运算，就会返回逻辑值0，即x不是A中的某个元素。
拓展：如果A是一个数组，那么命令length(A) == 0 的返回结果和isempty(A)的返回结果一样，MATLAB推荐大家使用后者判断A是否为空数组[ ]，后者的运行效率更高。
（2）unifrnd函数（★★★☆☆）
unifrnd 函数可以生成任意区间内均匀分布的随机数，该函数需要统计和机器学习工具箱Statistics and Machine Learning Toolbox。
例子：
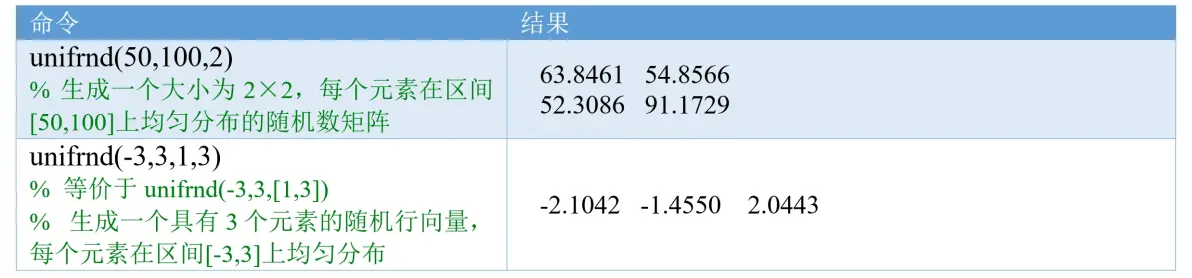
拓展：a + (b - a) * rand(m,n)等价于unifrnd(a,b,[m,n])或unifrnd(a,b,m,n).
（3）normrnd函数（★★☆☆☆）
normrnd函数可以生成正态分布的随机数，该函数需要统计和机器学习工具箱Statistics and Machine Learning Toolbox。（注意：randn只能生成标准正态分布的随机数）
例子：
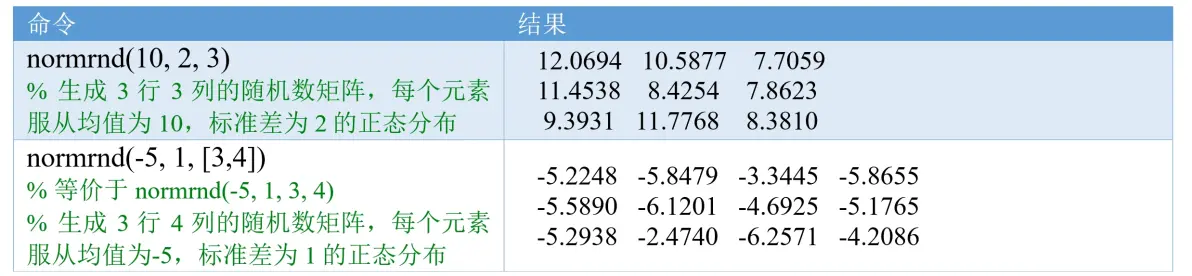
拓展：p + q*randn(m,n)等价于normrnd(p,q,[m,n])或normrnd(p,q,m,n).
（4）fibonacci函数（★☆☆☆☆）
fibonacci函数可返回斐波那契数列，该函数需要符号数学工具箱Symbolic Math Toolbox。
例如返回斐波那契数列的前十项可以使用代码fibonacci(1:10)
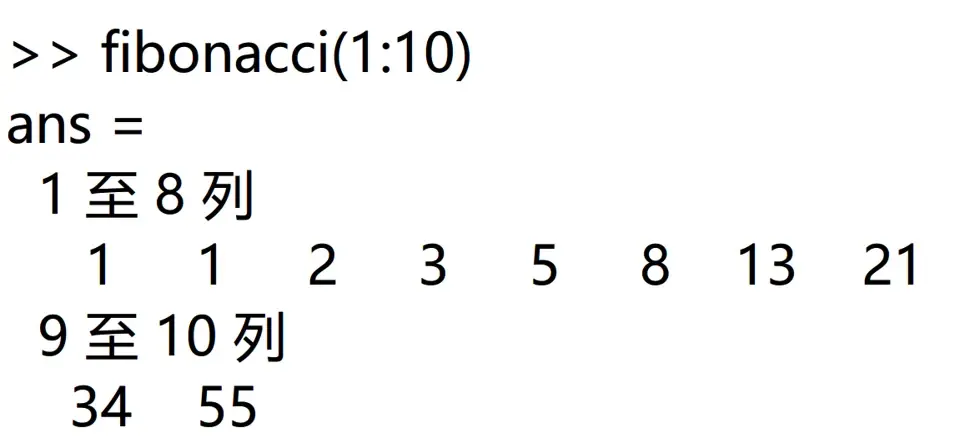
返回斐波那契数列的第50项可以使用代码fibonacci(50)
另外，斐波那契数列有通项公式：
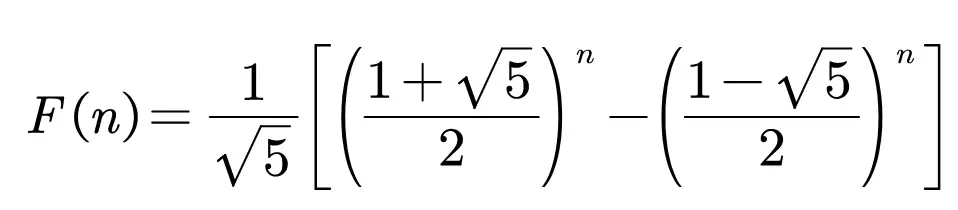
我们也可以使用通项公式进行计算。
例如计算斐波那契数列前10项的代码为：
fib_10 = 1/sqrt(5)*(((1+sqrt(5))/2).^(1:10)-((1-sqrt(5))/2).^(1:10))
（5）factorial函数（★★★☆☆）
factorial函数用于计算阶乘，如果n是一个正整数，那么factorial(n)就是计算n!。
例如我们计算3的阶乘和10的阶乘：
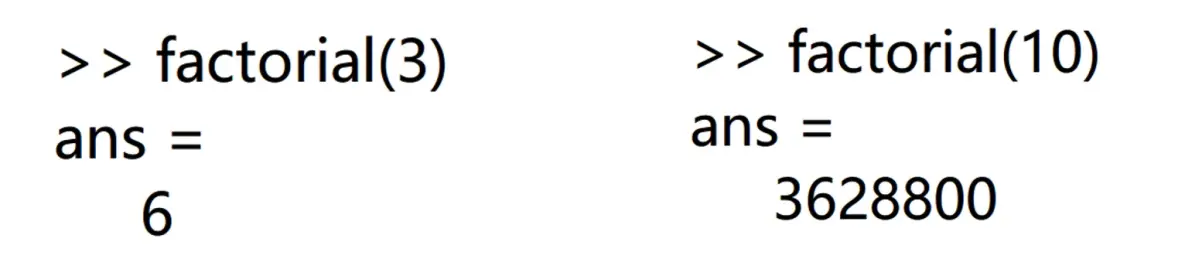
拓展：n为正整数时，命令prod(1:n)也可以计算n的阶乘。
（6）randperm函数（★★★★★）
randperm函数是一个非常有用的函数，它能够将一个数字序列进行随机打乱。它有两种主要的使用方法：
用法1：randperm(n)可以将向量1:n中元素的顺序随机打乱，生成一个长度仍为n的新向量，因此所有可能出现的情况共n!种（全排列）。例如，当你运行randperm(4)时，你可能得到[1 4 3 2]，也可能得到[3 2 4 1]。
用法2：randperm(n,k)表示从打乱的1:n序列中随机的选择k个数出来，显然这k个数都不相同，且k要小于等于n。例如，当你运行randperm(10,3)时，你可能得到[5 3 10]，也可能得到[6 1 8]。
randperm函数在实际的场景中应用的非常广泛，第三章课后练习挑战篇中的第五题举了几个例子，大家一定要看本讲义最上方的作业讲解视频学习。
（1）模拟商品推销员访问城市（旅行商问题、TSP）
（2）模拟课堂上随机选取同学答题
（3）模拟抽奖能获得多少金额
（4）模拟斗地主游戏为地主和农民发牌
注意：randperm(n,k)和randi(n,k,1)的区别在于：randperm相当于无放回的抽样，而randi相当于有放回的抽样。因此，randperm函数返回的结果中的各元素都不相同，而randi函数返回的结果中的各元素可能相同。
拓展：对randperm函数背后原理感兴趣的同学可以自行搜索Fisher–Yates shuffle 算法（洗牌算法）。
（7）randsample函数（★★★☆☆）
rand取自单词random，翻译成中文表示随机；单词sample翻译成中文表示样本，因此根据字面意思理解randsample函数用于生成随机样本，它是randperm函数的进阶版本，该函数需要统计和机器学习工具箱Statistics and Machine Learning Toolbox。
下面我们介绍它的主要用法：
（1）y = randsample(n,k) 返回从整数1到n中无放回随机均匀抽取的k个值。
y = randsample(n, k)等价于y = randperm(n, k)，只不过randsample返回的是列向量，randperm返回的是行向量。
（2）y = randsample(n,k,true) 返回从整数1到n中有放回随机均匀抽取的k个值。
y = randsample(n, k, true) 等价于y = randi(n, k, 1)。
（3）y = randsample(population,k) 返回一个向量，其中包含从向量 population 的值中无放回随机均匀抽取的 k 个值。
（4）y = randsample(population,k,true) 返回一个向量，其中包含从向量 population 的值中有放回随机均匀抽取的 k 个值。
（5）y = randsample(n,k,true,w) 使用长度为 n 的非负权重向量 w 来确定整数 i 被选为 y 的元素的概率（这里一定是有放回的抽样，因此第三个输入参数只能为true）。
以下是权重向量w的介绍：
（6）y = randsample(population,k,true,w)使用与向量 population 长度相同的非负权重向量 w 来确定值 population(i) 被选为 y 的元素的概率（这里一定是有放回的抽样，因此第三个输入参数只能为true）。
（8）datasample函数（★★☆☆☆）
datasample函数是randsample函数的进阶版，和randsample函数相比，datasample函数还可以随机抽取矩阵的行或者列。函数可以设置是有放回还是无放回的抽取，也能指定权重。
下面我们通过代码了解datasample函数常见的用法：
dim等于1时，表示沿着行方向进行随机抽取，此时得到的是随机的行；dim等于2则表示沿着列方向进行随机抽取，此时得到的是随机的列；另外，输入参数 'Replace' 后面的false表示无放回的随机抽样， true则表示有放回的随机抽样。
当然，我们也可以使用randsample函数来实现随机抽取矩阵的行或者列，只需要随机生成行或列的下标索引即可。因此datasample函数可以由randsample函数代替。
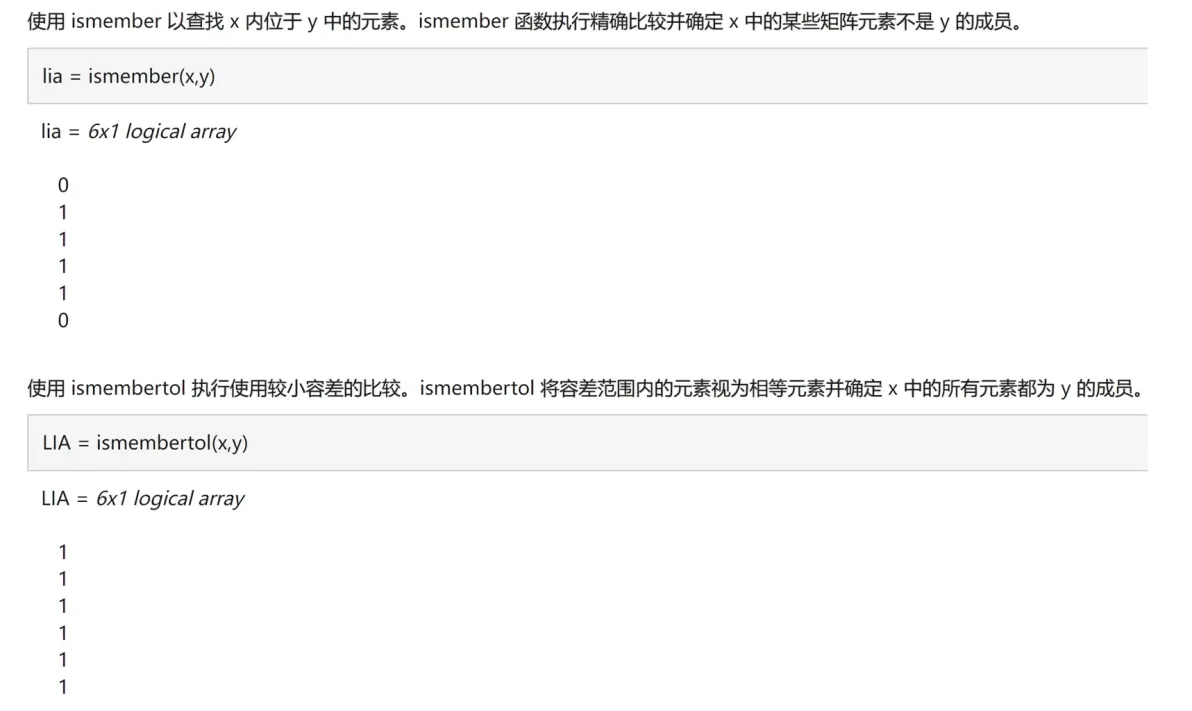
（9）ismembertol函数（★★☆☆☆）
ismembertol函数和ismember函数的功能类似，它在比较元素是否相等时考虑了一定的容差。
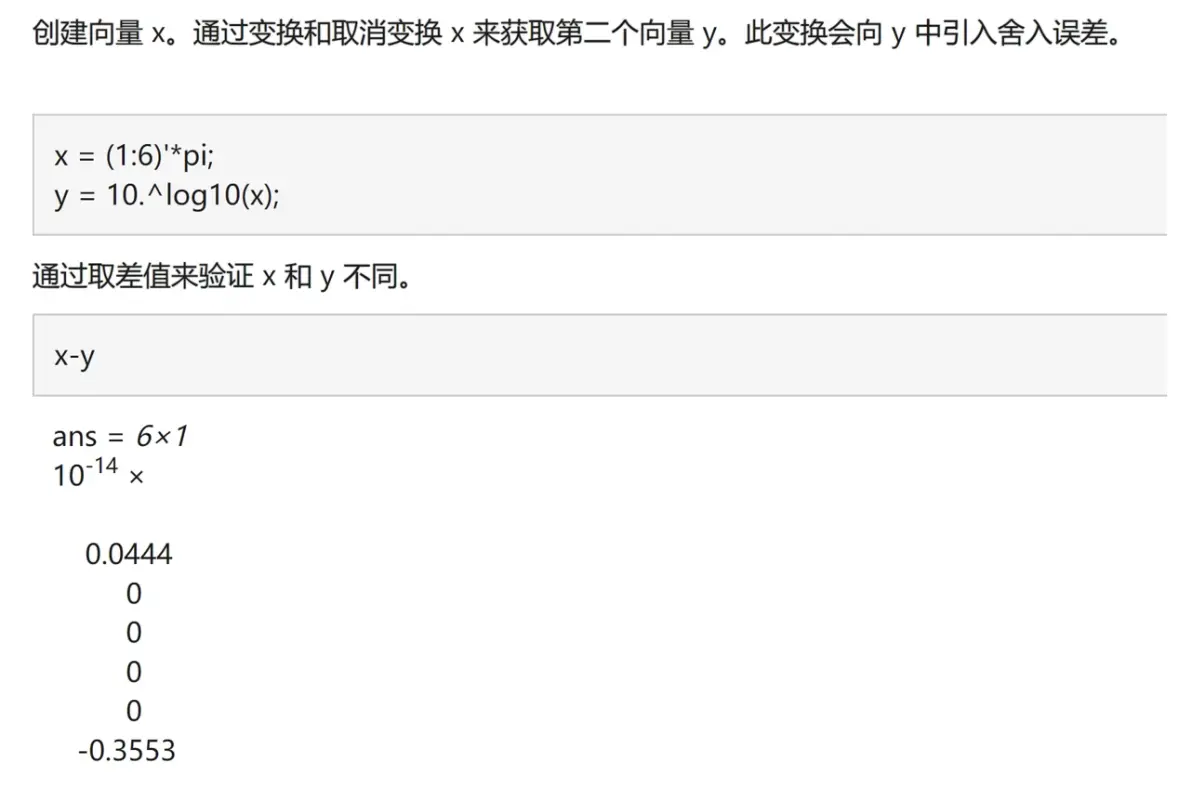
我们可以看官网这个例子：
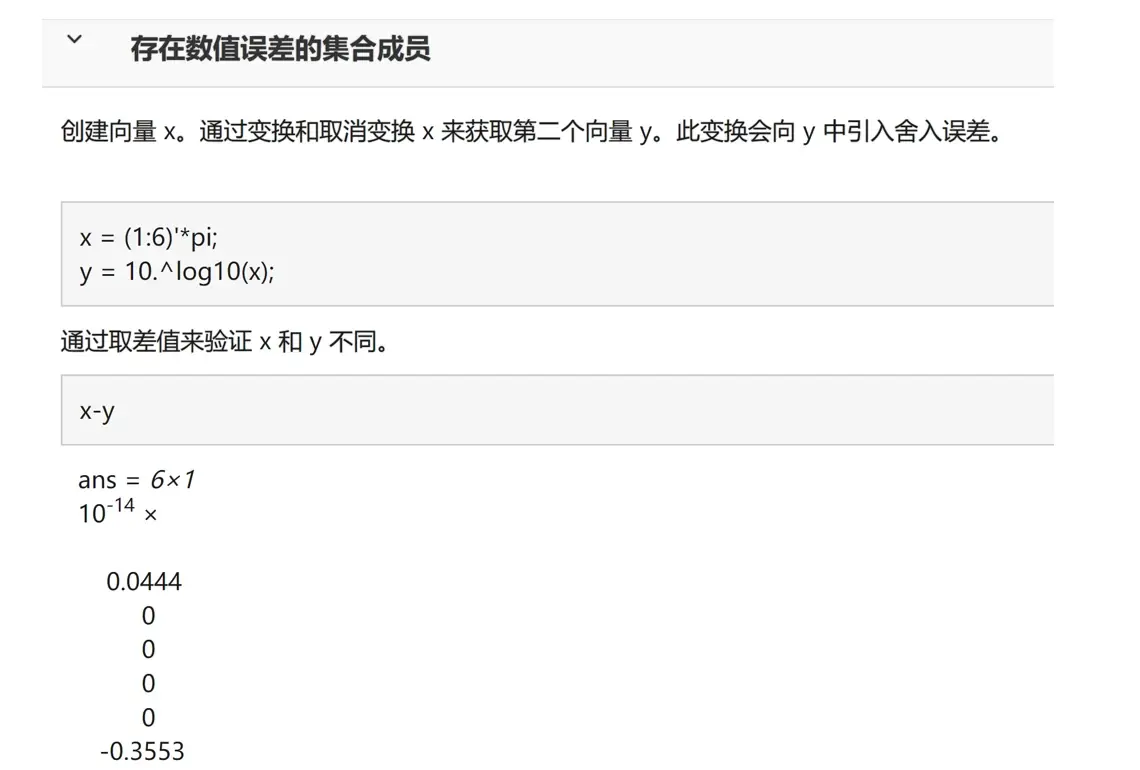
理论上x和y是相等的，因为.
但由于浮点数计算带来的误差，x和y的部分元素之间有非常小的差异。
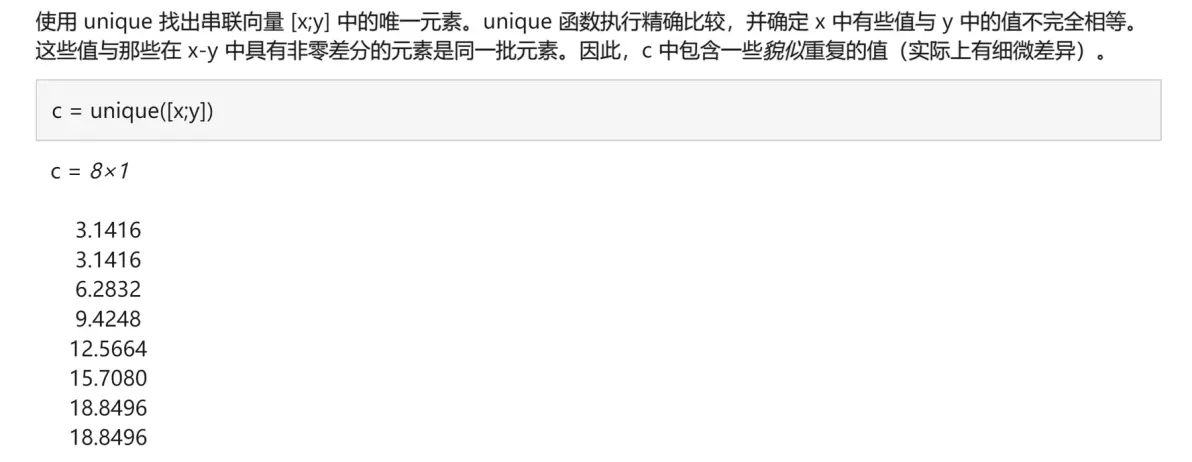
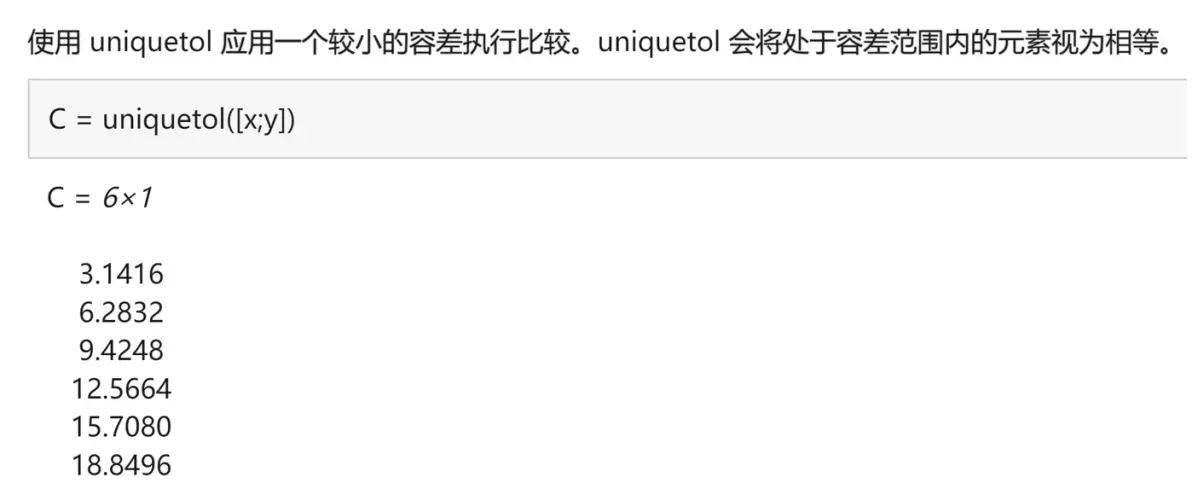
（10）uniquetol函数（★★☆☆☆）
uniquetol函数和unique函数的功能类似，它在比较元素是否相等时考虑了一定的容差。
我们可以看官网这个例子：
（11）prctile函数（★★★☆☆）
prctile函数可计算百分位数。百分位数（percentile）是统计学术语，若将一组数据从小到大排序，并计算相应的累计百分点，则某百分点所对应数据的值就称为这个百分点对应的百分位数。你可以认为将一组数据升序排列后，处于位置的数就是这组数据的第百分位数，我们记为。
例如，大家熟悉的中位数就是排序后处于中间位置的数，因此中位数也被称为第50百分位数，我们可以记为，有时也记为.
下四分位数则是位于排序后的数据25%位置上的数，我们用Q1表示；上四分位数则是处在排序后的数据75%位置上的数，我们用Q3表示。
下面我们来看prctile函数的使用方法：
（1）Y = prctile(X,p) 根据区间 [0,100] 中的百分比 p 返回数据向量或数组 X 中元素的百分位数。
（2）Y = prctile(X,p,dim) 返回运算维度 dim 上的百分位数。
如果X是一个矩阵，那么dim等于1时表示沿着行方向进行计算，得到每一列元素的百分位数；dim等于2时表示沿着列方向进行计算，得到每一行元素的百分位数。
（12）meshgrid函数（★★★★☆）
meshgrid函数可以基于向量x和y中包含的坐标来返回二维网格坐标。
举个具体的例子帮助大家理解：假设x轴坐标上的取值是[0 1 2 3 4]，y轴坐标上的取值是[0 1 2 3]，现在请使用x轴坐标和y轴坐标共同创建下图所示的二维网格坐标：
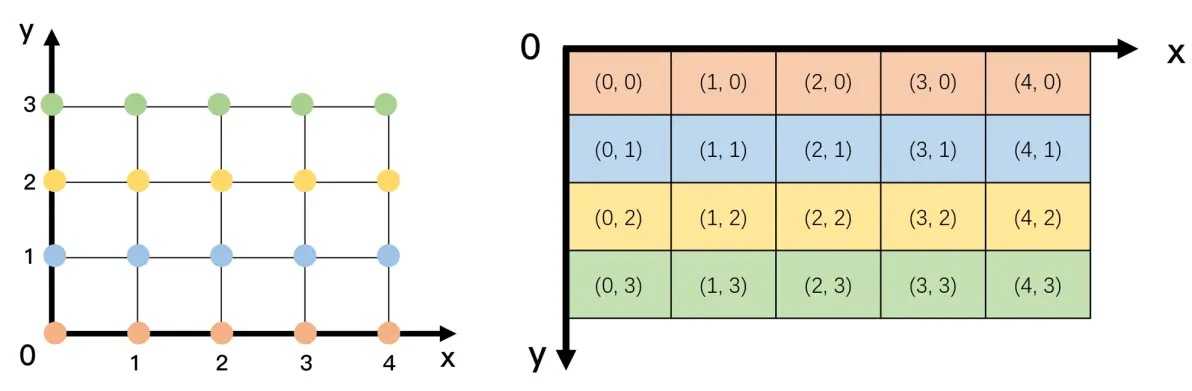
分析：x轴坐标上的取值有5种，y轴坐标上的取值有4种，将取值进行组合有20种，因此上方左图有20个交点，每个交点对应一个网格坐标。如果指定交点的排列顺序为沿着x轴的正方向和y轴的正方向，这样就能表示这20个交点的网格坐标，结果在上方右图中。
在MATLAB中，会将点的坐标(x, y)拆分成横坐标矩阵和纵坐标矩阵分别保存，我们可以使用meshgrid函数得到这两个矩阵：
进一步地，如果我们想在这20个交点构成的二维网格上计算二元函数的值，我们可以使用下面的代码：
另外，如果我们只给meshgrid函数一个输入变量，那么命令[X,Y] = meshgrid(x) 得到的结果和 [X,Y] = meshgrid(x,x)得到的结果完全相同。
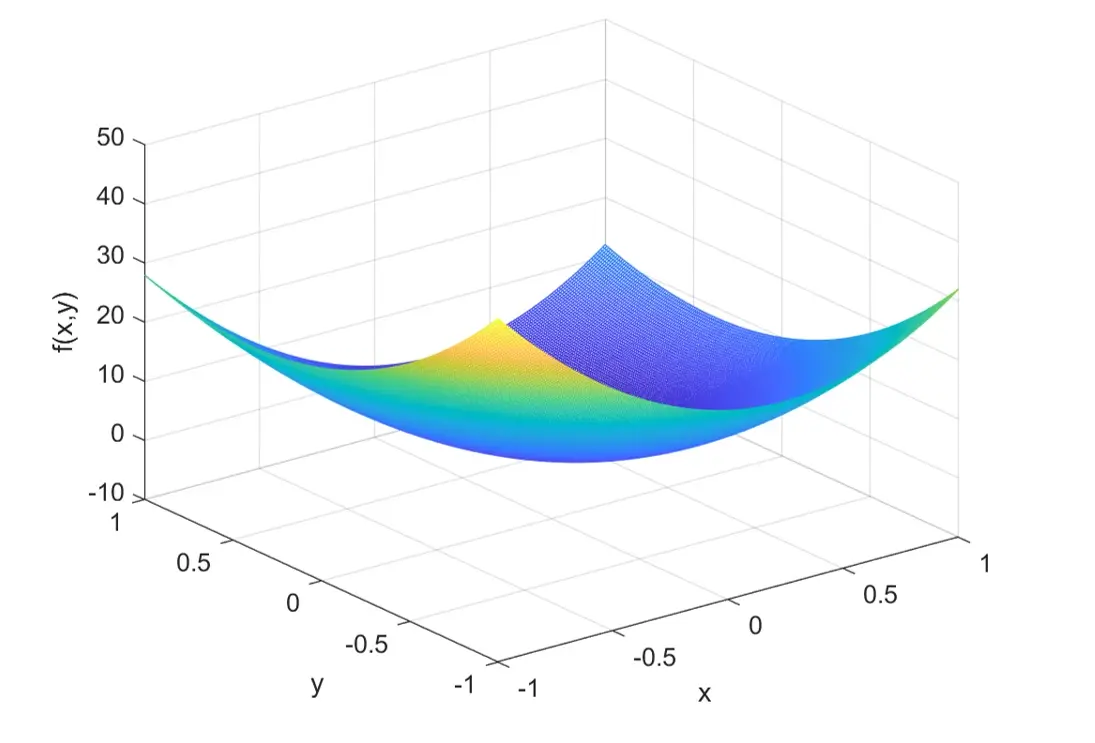
事实上meshgrid函数在三维图的绘制中用的比较多，我们先给大家看个例子，后续章节中会系统讲解三维图的绘制方法。
绘制 在𝑥和𝑦都位于区间[−1,1]上的图形。
d = 0.01;
x = -1:d:1;
y = -1:d:1;
[x,y] = meshgrid(x,y); % 直接用meshgrid函数返回的x和y矩阵替换原来的输入变量x和y
z = x.^3 - y.^3 + 18 * x.^2 + 12 * y.^2 - 9 * x - 9 * y;
close all
mesh(x,y,z) % mesh函数可用来绘制三维网格图，你也可以改成surf函数来绘制三维曲面图
xlabel('x');ylabel('y');zlabel('f(x,y)')
（13）rng函数（★★★★★）
rng函数可用来设置随机数种子，这样能生成可重复的随机数。
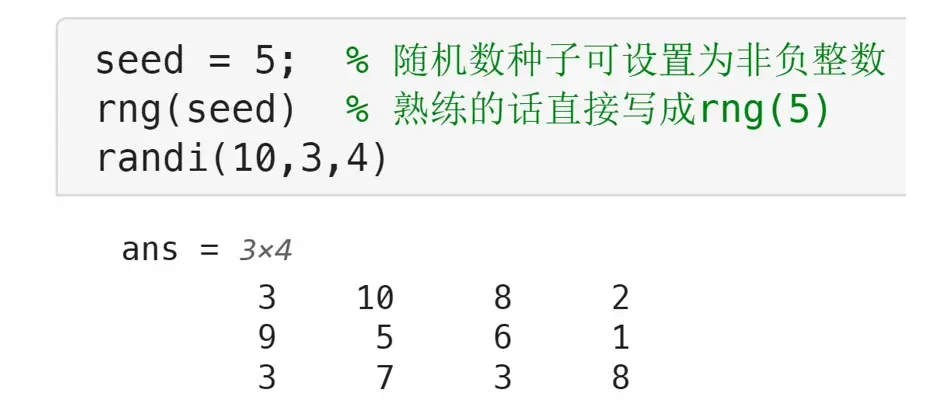
使用随机数生成函数(例如rand, randi等)之前，使用rng(seed)命令设置随机数种子，这样能保证生成的随机数被固定下来。设置不同的随机数种子生成的随机数通常都不相同。
拓展：每次重新启动 MATLAB 时，随机数生成器均复位到相同的状态，这样使用生成随机数的命令会返回相同的结果。我们可以使用 rng('shuffle') 命令，它可以根据当前的时间使用不同的种子重新设定生成器的种子，这样能避免重复生成相同的随机数。
（14）poissrnd函数（★★☆☆☆）
poissrnd函数用于生成泊松分布的随机数，该函数需要统计和机器学习工具箱Statistics and Machine Learning Toolbox。
设随机变量X所有可能的取值为0,1,2,...，而取各个值的概率为：
其中λ>0是常数，则称随机变量X服从参数为λ的泊松分布，可以证明：参数为λ的泊松分布的期望和方差均为λ.
泊松分布适合于描述单位时间内随机事件发生的次数，参数λ就是单位时间内随机事件的平均发生次数，有时也被称为事件发生的速率。
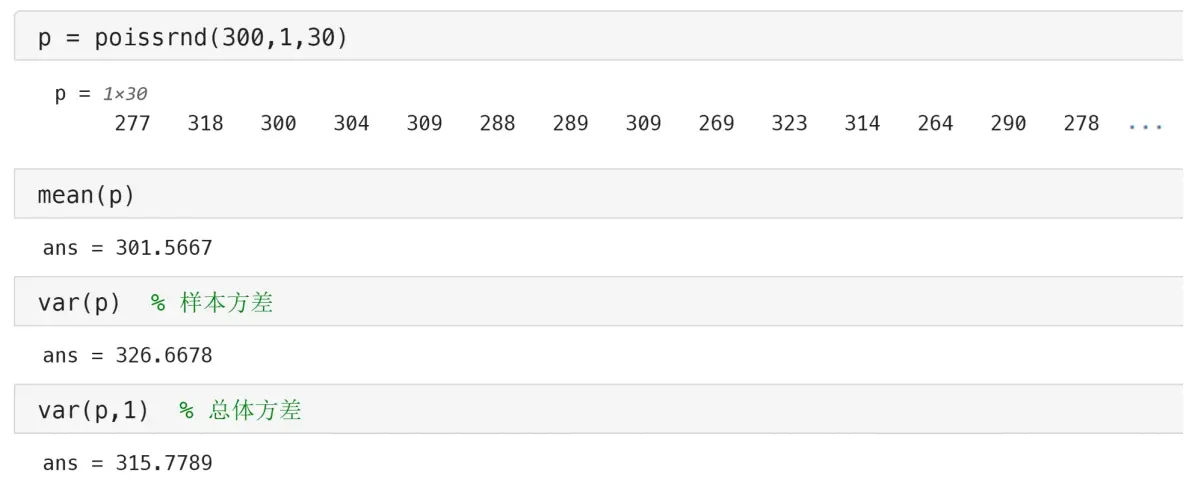
例子：假设某商店每天的客流量服从λ=300的泊松分布，请模拟这个商店最近一个月每天的客流量，并计算均值和方差。
（15）exprnd函数（★★☆☆☆）
exprnd函数用来生成指数分布的随机数，该函数需要统计和机器学习工具箱Statistics and Machine Learning Toolbox。
若连续型随机变量X的概率密度函数为：
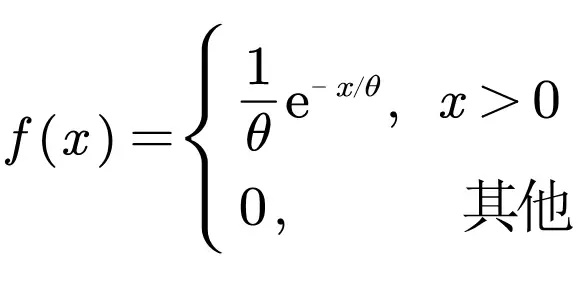
其中>0为常数，则称X服从参数为的指数分布。
若X服从参数为的指数分布，则记为X~EXP() ，可以证明X的期望为
，方差为
.
如果使用随机变量X表示一件物品的寿命，例如灯泡的使用寿命，那么的含义可以代表平均寿命。
例子：假设某工厂生产的二极管的使用寿命服从均值为2000小时的指数分布，请随机生成1000个二极管的使用寿命，并计算均值和方差（结果请四舍五入）。
拓展：有些教材也使用下面的概率密度函数定义指数分布：
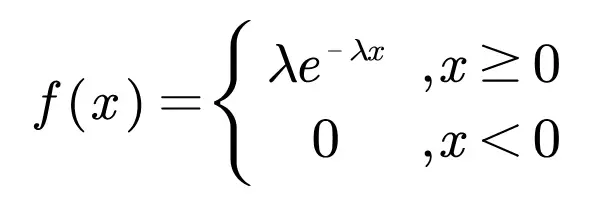
这种定义方法和上面的定义方法是等价的，此时λ=1/.
（16）nchoosek函数（★★★☆☆）
nchoosek函数主要用来计算组合数，也能返回从向量v中抽取k个元素的所有组合。
例如计算：
下面是nchoosek函数的第二种用法：返回从向量v中抽取k个元素的所有组合。
（17）perms函数（★★★☆☆）
perms函数可用来返回向量v中各元素所有可能的排列情况。
拓展：（1）如果v中有k个元素，那么返回的矩阵的行数为k的阶乘；（2）randperm(n)得到的结果实际上就是从perms(1:n)返回的矩阵中随机的抽取一行。
下一篇文章：
更多文章可点击下方合辑：
155-2731-8020
