注意:绿色高亮为易错或认识难点,黄色高亮为新知识;
W1S2-变量类型(在W2S2讲解)
W2S2.逻辑运算+字体设置 P6 - 36:02 饱和
int8存储最大整数为127(∵其为-128...-1,0,1...127),
int16同理;
uint8最大数为2^8-1;
int8最大数为2^8/2-1;
W1S4-常数&随机数
1.当虚数单位i或j被占用时,可以在前面加上‘1’使i或j仍为虚数单位;
2.产生随机数时,使用“rng('shuffle')”可以保证随机种子不同,产生的随机结果也就不同;
3.rng函数使用括号内的非负取整部分;
4.randn产生正态分布随机数,randi([a,b])产生a到b的整数随机数。
5.Inf表示无穷,NaN表示未定义数;
W2S1-字符型变量简介
详见C语言ascii码相关概念
W2S2-逻辑运算
1.‘==‘表示判断是否等于;’~=‘表示判断是否不等于;
2.’&&‘与’||‘的使用同C语言(注意:&&左0则不执行右;||左1则不执行右——“短路运算”),‘~’表示非;
3.xor(A,B)为语句A与B当且仅当只有一个正确时返回1;
4.运算符优先级如下:

5.注意:连续比较时应当注意顺序:5>4>3➡(5>4)>3➡1>3➡0;
6.浮点数计算后比较涉及舍入误差,故经常使用两者差的绝对值来比较;
W2S2.逻辑运算+字体设置 P6 - 37:36 浮点数比较
W2S3-基本函数
1.sin()输入弧度,sind()内输入角度;
2.fix()取整去掉小数部分,floor向负无穷取整,ceil向正无穷取整,round()向最近整数取整(四舍五入);
3.round(C,x)保留C的x位小数;
4.mod(A,B) == A除以B的余数,mod&rem不同点查看help;
5.sign(x)返回x的符号;
6.sqrt()求平方根,nthroot(x,y)求x的y次方根;
7.deg2rad()角度转换弧度,rad2deg()同理;
8.log()默认以e为底,logn()表示以n为底;
9.exp(x)表示e的x次方;
W2S3-行向量
1.[]或用”x:d:y“输入从x到y,公差为d的等差行向量,d省略则默认公差1;
2. linspace(x1,x2,d) 建立从x1到x2,有d个数的等差数列;logspace(x1,x2,d)建立从10^x1到10^x2,有d个数的等比数列;
3.[u v]将两个向量组合;
4.u(x)访问u的第x个元素,matlab中数组编号以1开头;
5.u([x y])访问u的第x与第y个元素并以向量形式返回;
6.u(end-n)返回倒数第n个数,u(a:end-n)返回第a个到倒数第n个数;
W2S4-列向量&矩阵
1.[x;y;z]分号表示一行结束,共轭转置为单引号;单纯转置为.'
2.返回值与原向量相同形式,而非指标向量;
3.rand(x,y)输出x行y列随机数方阵,randi([x,y],a,b)输出从x到y的随机整数a行b列矩阵;
4.zeros()0矩阵,ones()1矩阵,eye()单位矩阵,diag()对角矩阵;
5.diag(,n)表示第n个对角线元素赋前面的值;
6.访问值时线性下标:

7.W2S4.列向量+矩阵 P8 - 39:08 矩阵大小相关函数
length()返回max{行数,列数};size()返回行数,列数;[n_row,n_col]=size()行数&列数分别赋值;numel()返回元素数;
8. matlab中0,Inf,NaN理解成数列极限;
W3S1-向量&矩阵常用函数
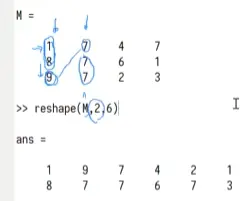
1.reshape()改变矩阵的形式且原矩阵不变;元素数必须一致;
2.flipud()纵向翻转,fliplr()横向翻转;flip()以列向量翻转(flipud);
3.rot90()逆时针旋转90°;
4.repmat(A,x,y)-repeat matrix将A纵向复制x次,横向复制y次;
repelem(A,x,y)-repeat element

5.空矩阵-用以存储数组,NaN(x,y)产生x行y列空矩阵;

掷骰子
W3S2-向量运算&矩阵运算
1.三维数组用T(:,:,k),k=1,2,3...;(把纸叠在一起)
2.min()返回一维向量最小值,矩阵每一列最小值,max()同理;
3.sum()返回所有元素和,prod返回所有元素之积(向量情况),矩阵看help;
4.cumsum()&cumprod()&cummin()&cummax()

5.diff()➡x(2)-x(1),x(3)-x(2)……;
6.矩阵运算 .*为两个数组对应元素相乘,./同理,.^;

W3S3-逻辑向量&逻辑矩阵
0.产生逻辑数组;
1.v(v>x)返回v中所有大于x的元素;
2.logical()强制转换成逻辑数组;或者在后面跟修饰'logical';
3.any()逻辑数组中是否至少有一个是真值,all()同理;
4.find()返回逻辑数组中为真值的数字位置,find(x,k)x中的前k个真值位置;
5.all(x1==x2)比较x1与x2对应位置元素是否相同;isequal(x1,x2)类似;
6.例题1

剔除vec中所有负数
P.S.>>第二行语句将负数赋予空值,即剔除;
7.例题2
W3S3.逻辑向量和逻辑矩阵 P11 - 32:45 例2
numel(find(differ(V) == 1))
sum(differ(V == 1))更简洁;
W3S3.逻辑向量和逻辑矩阵 P11 - 41:14 例2.2
找出数组中所有1➡2的次数
法(1)将0改成NaN;
法(2)
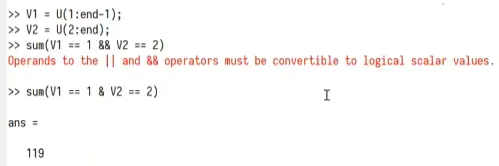
8.对于向量用&连接,标量&&连接;
W3S4-矩阵乘法
1.".^2"元素自身平方;点积".*"后求和或转置乘;叉积cross();
2.希尔伯特矩阵hilb(),帕斯卡矩阵pascal(),幻方阵magic();
3.[I,J]=ind2sub(size,ind)将线性下标转换成行、列序号;
W3S4-变量输出显示
1.disp();
W3S4.矩阵乘法+变量的输出和显示(上) P12 - 25:33 disp
2.num2str(,x)将整型,实型转换成字符串型并保留x位
3.fprintf()(C语言printf())
W3S4.矩阵乘法+变量的输出和显示(上) P12 - 36:54 fprintf
4.ctrl r注释ctrl t取消注释;
5."%+"正号有则输出符号;
W5S3
function被存储在同名文件中成为公共函数,跟在脚本后成为局部函数
W6S2
事先赋予变量空间提高计算效率

W7S4
1.同名静态变量在不同函数中的值不相互影响;
2.函数中才可以定义静态变量