离散时间序列频谱分析：MATLAB实现方法

摘要：在MATLAB上，用傅立叶变换、自相关函数法以及最大熵估计法对一组离散的时间序列进行谱分析，并作出对应的频谱图，进行比较。

关键词：离散时间序列，MATLAB，傅立叶变换，自相关函数法，最大熵估计（MESE）

               

1． 概述：

利用傅立叶变换，自相关函数法以及最大熵估计法对离散数据进行谱分析，找到数据的相关特性，并比较几种方法的特点。

 

2． 谱分析原理：

时间序列是以时间为参考基准进行记录的，从直观图上无法获得数据内部的基本特性，通过谱分析的方法，将时域的数据转换到频域上去，通过分析频域的特征来获取数据的特性，从而达到分析数据的目的。

 

可以用傅立叶变换、自相关函数法、最大熵估计三种方法，将时域的数据转换到频域上进行分析。

 

利用MATLAB的相关工具来实现。

 

3． MATLAB实现：

3.1数据说明：

程序中所用的数据是由

xn=A1*sin(f1*2*pi*n)+A2*sin(f2*2*pi*n)+e    （e为白噪声）

来产生的，其中：

n=0:0.001:1;

A1=4;

A2=4;

f1=25;

f2=50;

 

3.2MATLAB计算源程序

   1）创建.M文件，对离散时间序列用傅立叶变换和自相关法进行谱分析，代码如下：

      function FXi(data)

 

figure(1)

Fs=1000;

subplot(3,1,1);

t=0:1/Fs:1;

plot(1000*t(1:50),data(1:50));

xlabel('time(mm)')

title('一元时间序列直观图')

 

Y=fft(data,512)

Pyy2=Y.*conj(Y)/512;

f2=1000*(0:256)/512;

subplot(3,1,2);

plot(f2,Pyy2(1:257));

title('离散数据的傅立叶频谱图')

xlabel('频率（Hz）')

 

Fs=1000;

NFFT=1024;

Cx=xcorr(data,'unbiased');

Cxk=fft(Cx,NFFT);

Pxx=abs(Cxk);

t=0:round(NFFT/2-1);

k=t*Fs/NFFT;

P=10*log10(Pxx(t+1));

subplot(3,1,3);

plot(k,P);

title('谱估计的自相关函数法')

xlabel('频率（Hz）')

      2）创建.M文件，用最大熵法（MESE）对数据进行谱分析，代码如下：

         function MESE(data)

figure(2);

Fs=500;

NFFT=1024;

pyulear(data,20,NFFT,Fs);

       3)载入数据（要具有一定的长度），则输出结果为：

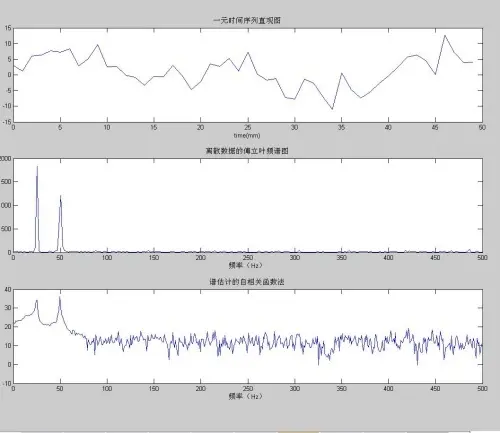
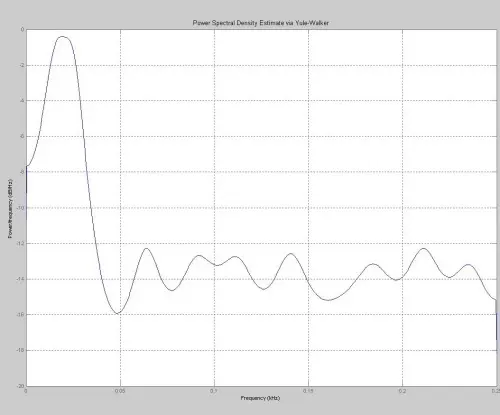
4． 结果与讨论：

由三种方法得到的频谱图表达的信息是类似的，明确的指出了离散数据中的信号特点，可以从谱分析图中得到数据的周期，与数据的原函数拟和的很好。但从图形的直观效果来看，用傅立叶转换的方法得出来的谱分析图对于数据特性的表达更明确，直观。