Fluent传热学习笔记：案例模型分享

物理量

热量：

热流量：

热流密度（热通量）：

方式：热传导、热对流、热辐射

热传导

傅里叶定律：

热流量：

热流密度：

热传导系数： 单位 

热对流

热流密度：

对流换热系数： 单位 

热辐射

黑体：能够吸收外来的全部电磁辐射，不会发生折射和透射。可以辐射放出电磁波，辐射能力和温度相关。

斯特潘-玻尔兹曼定律，黑体表面单位面积辐射出的总功率（物体的辐射度或能量通量密度）与黑体本身的热力学温度T （绝对温度）的四次方成正比，

其中，。

案例分析

1. 对流传热案例计算模型如下图所示，60°的热水以0.5的速度从上方口进入，25°的常温水以0.2的速度从左边口流入，出口采用压力出口。壁面设置为25°。

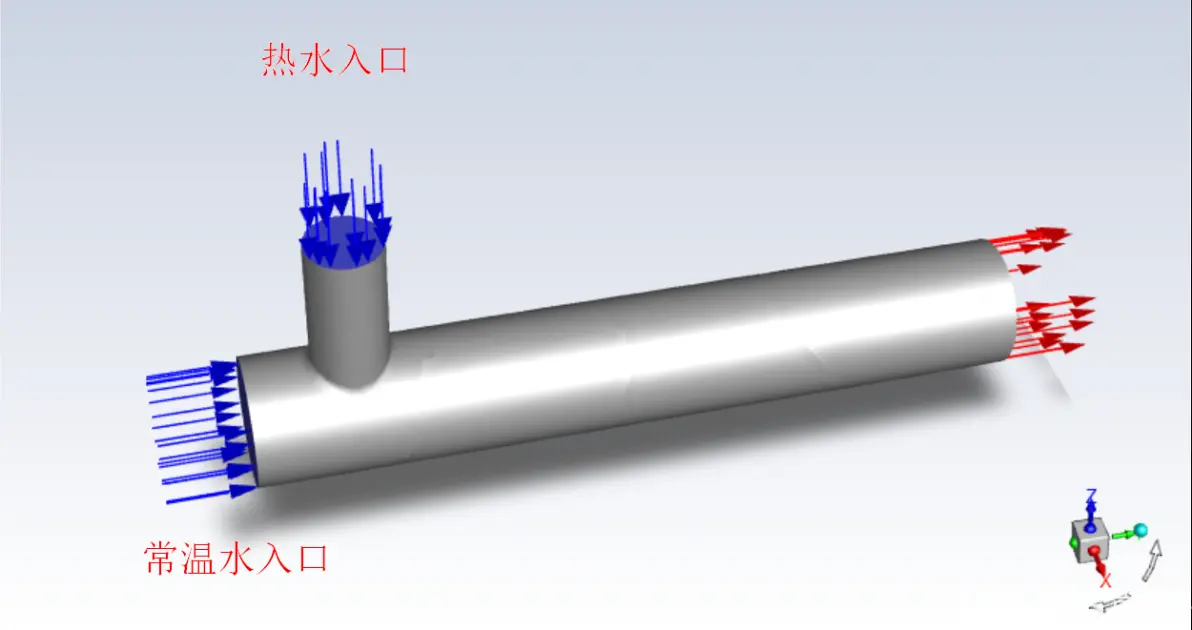
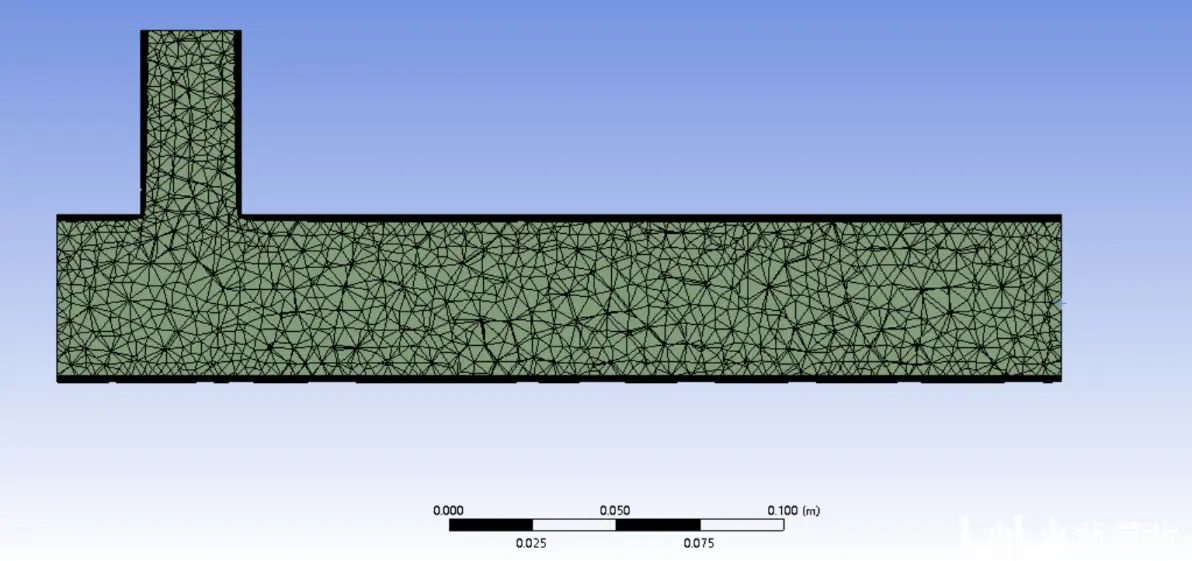
网格如下图，壁面附近添加边界层网格，传热问题涉及到温度边界层，一般要画边界层。

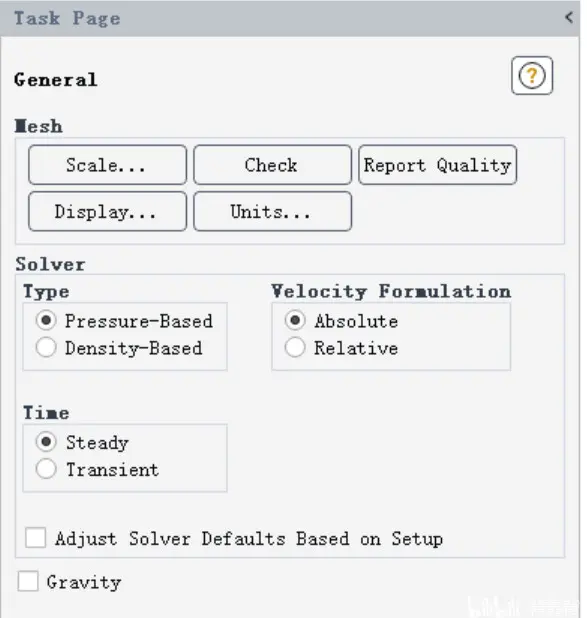
打开Fluent设置如下：

采用压力求解器，稳态求解。

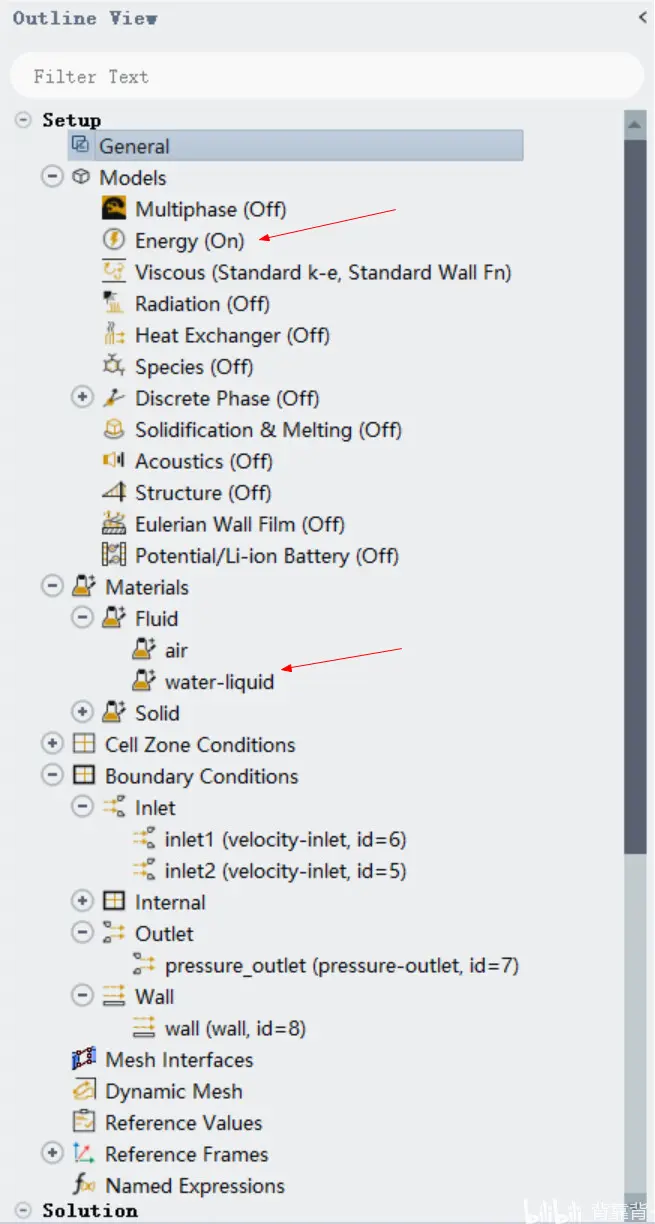
打开能量方程，选择湍流模型。材料添加液态水。

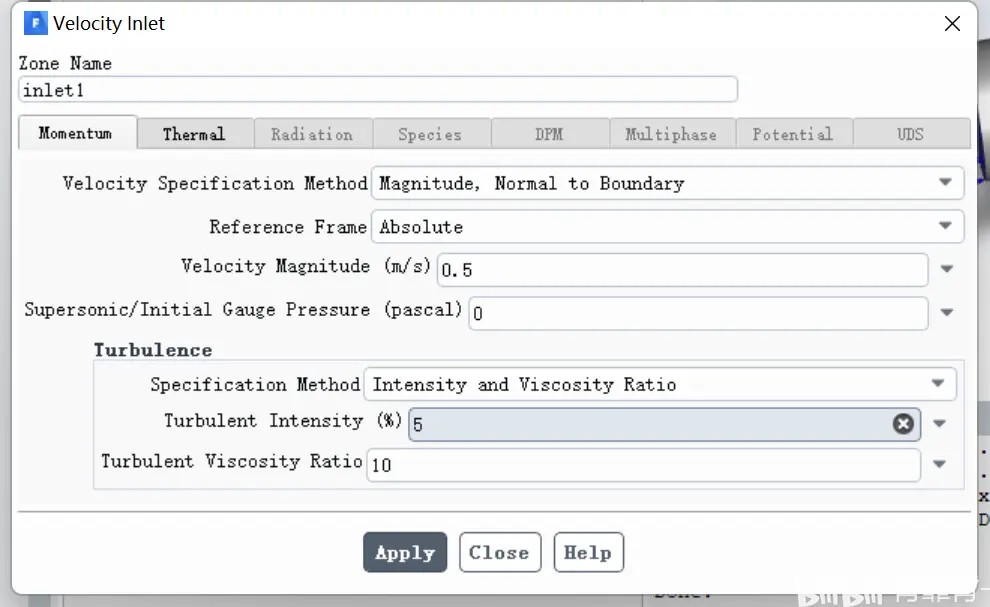
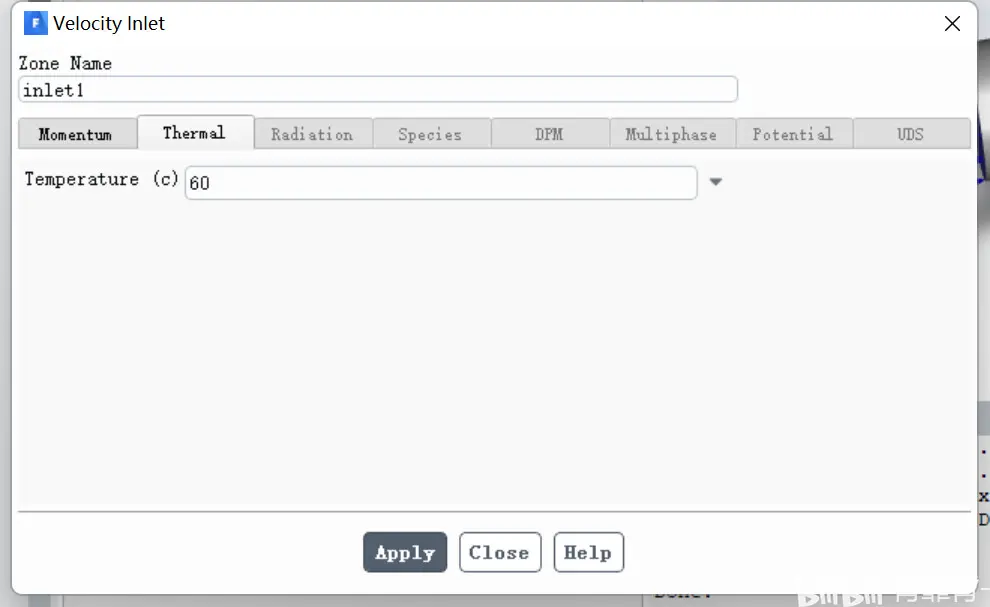
热水进口速度设置为0.5，温度设置为60°：

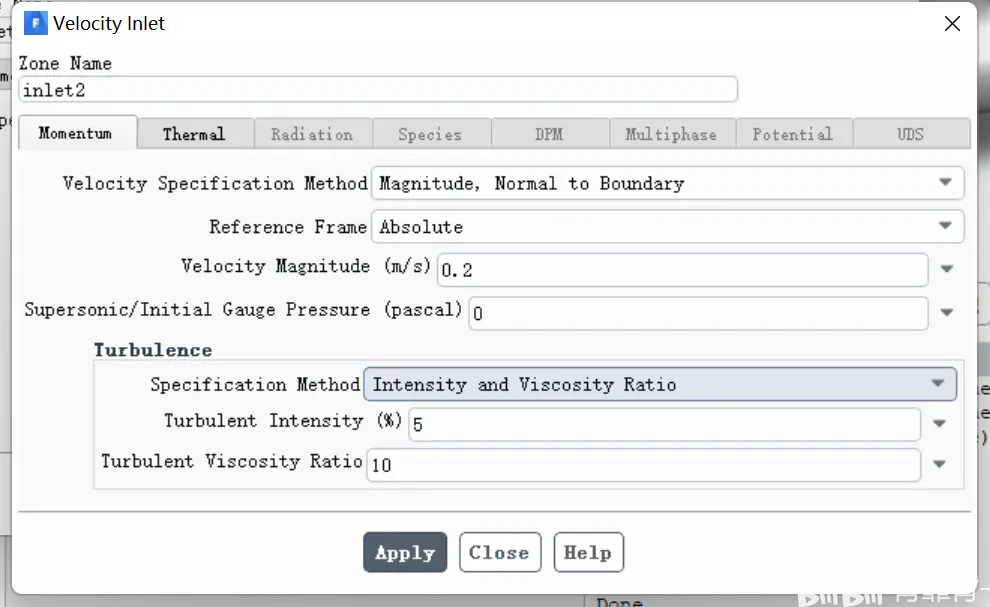
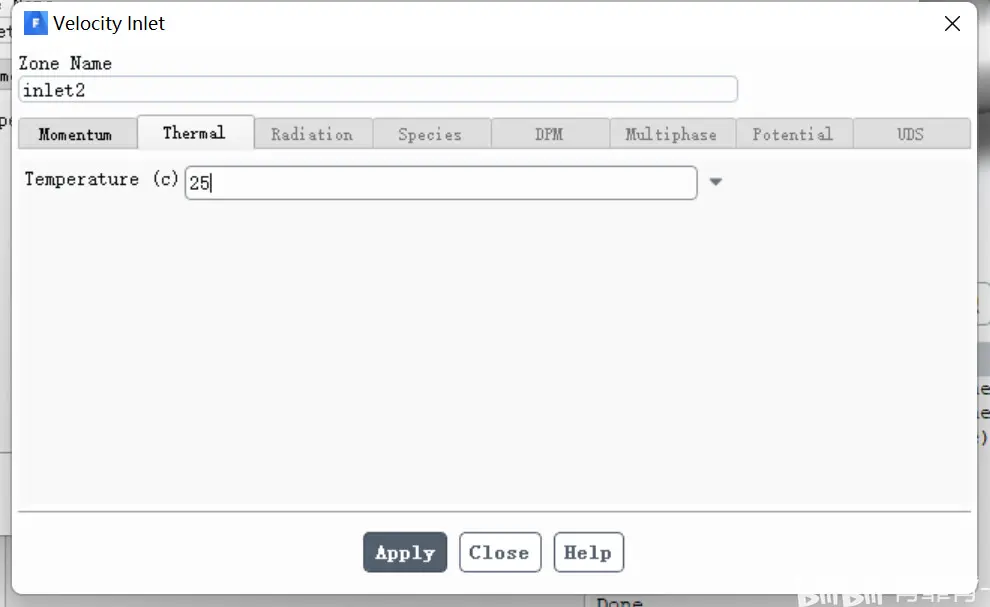
常温水入口速度设置为0.2，温度为25

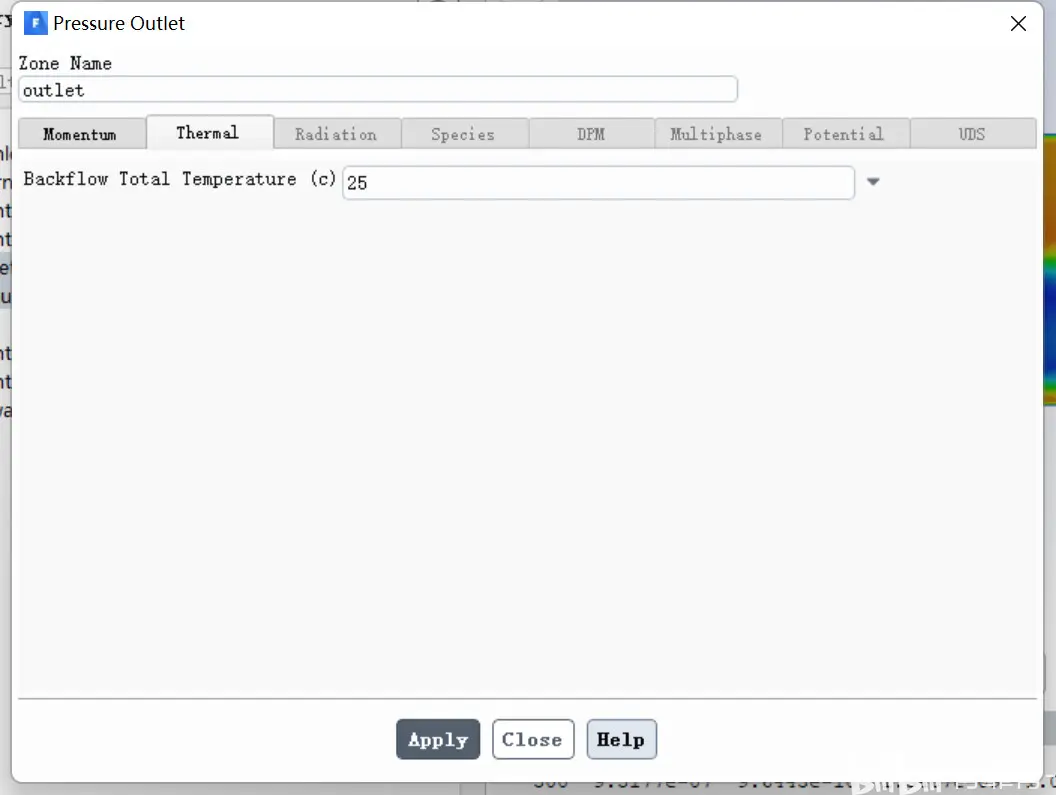
压力出口设置如下：

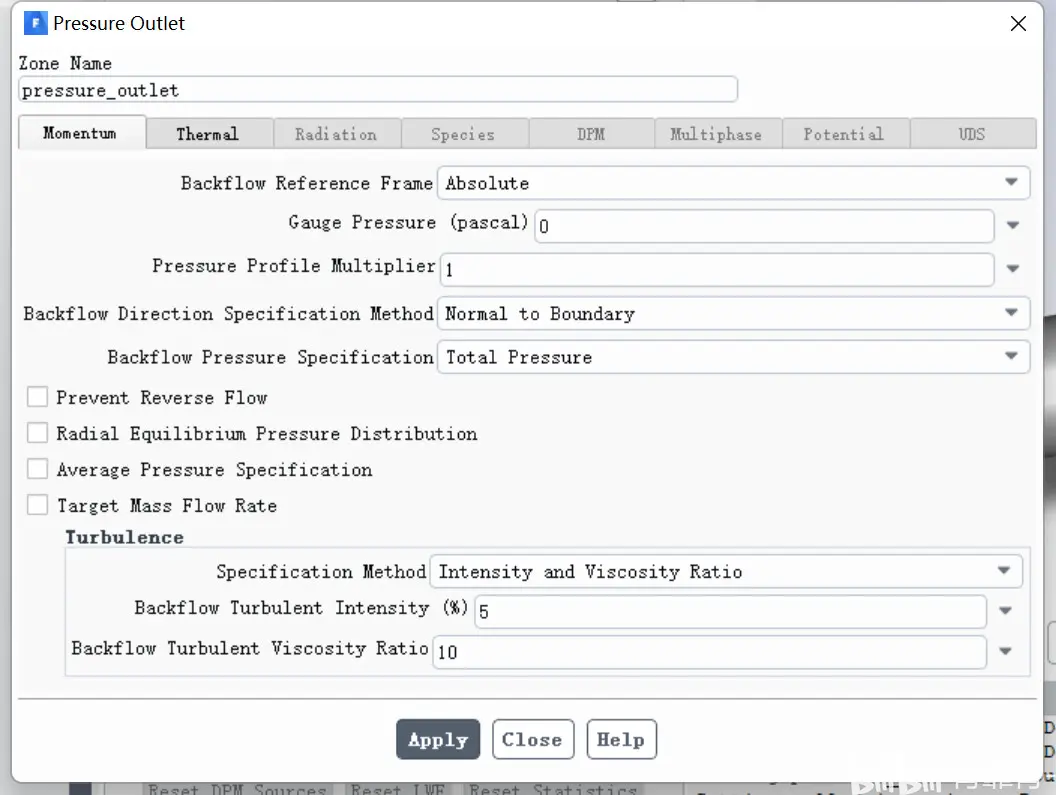
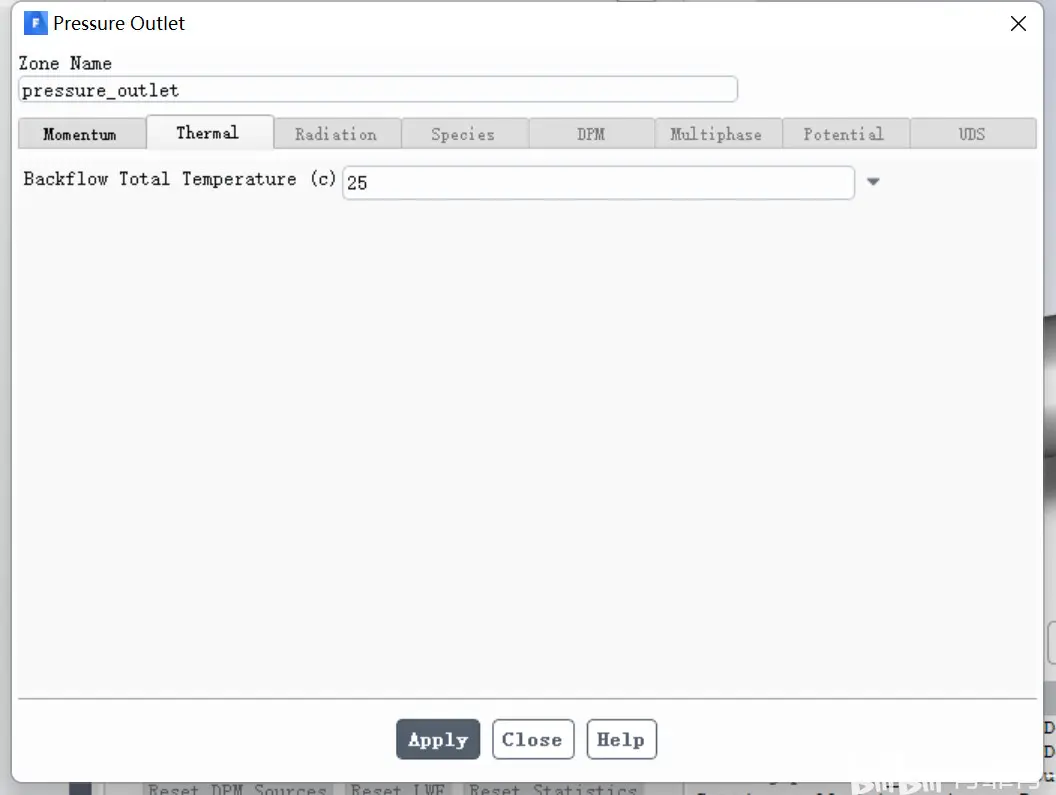
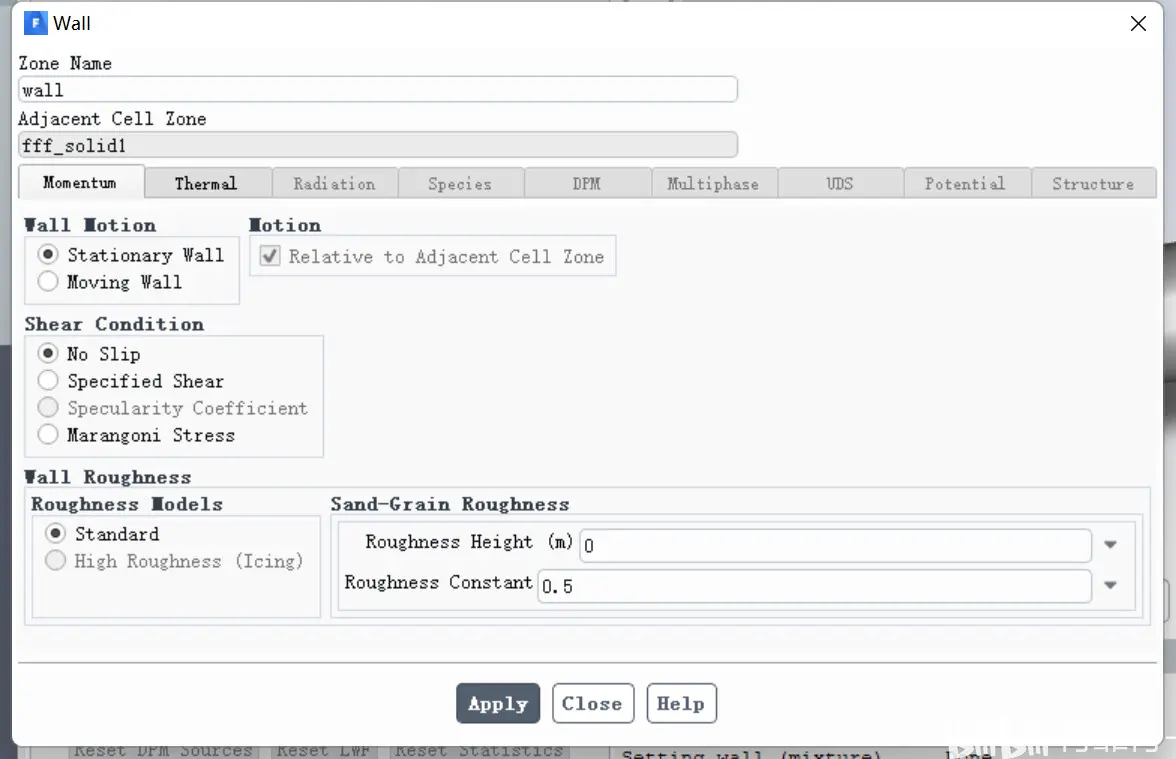
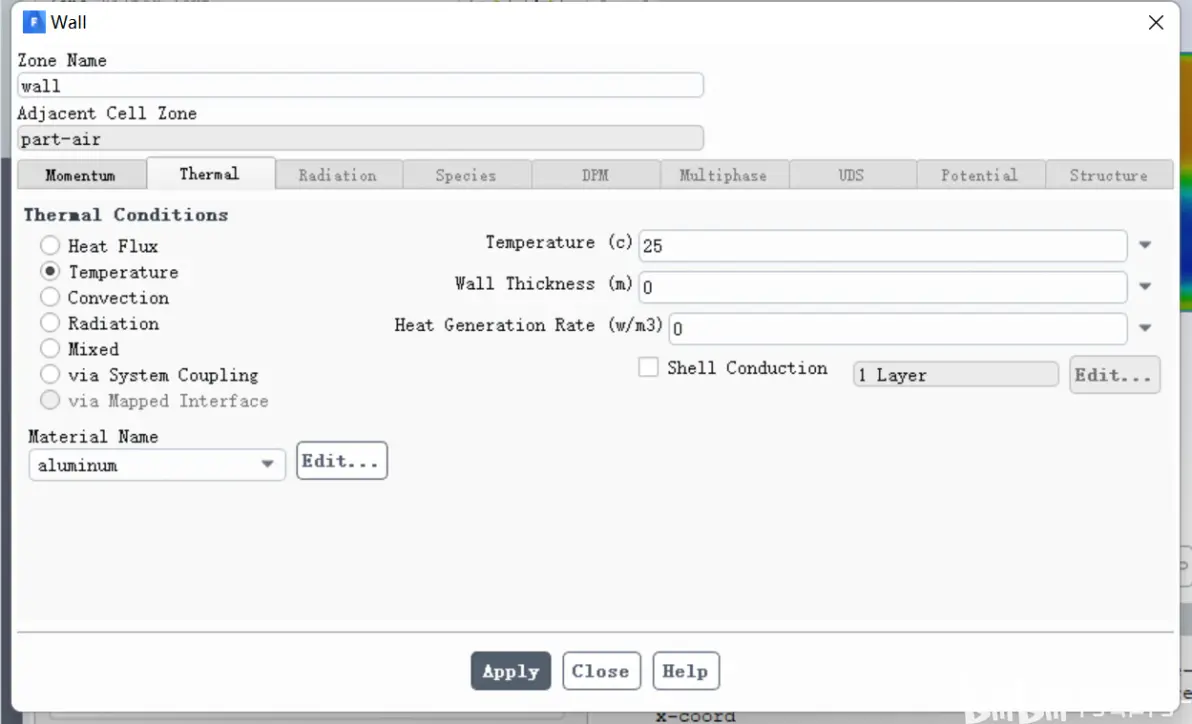
壁面设置如下：

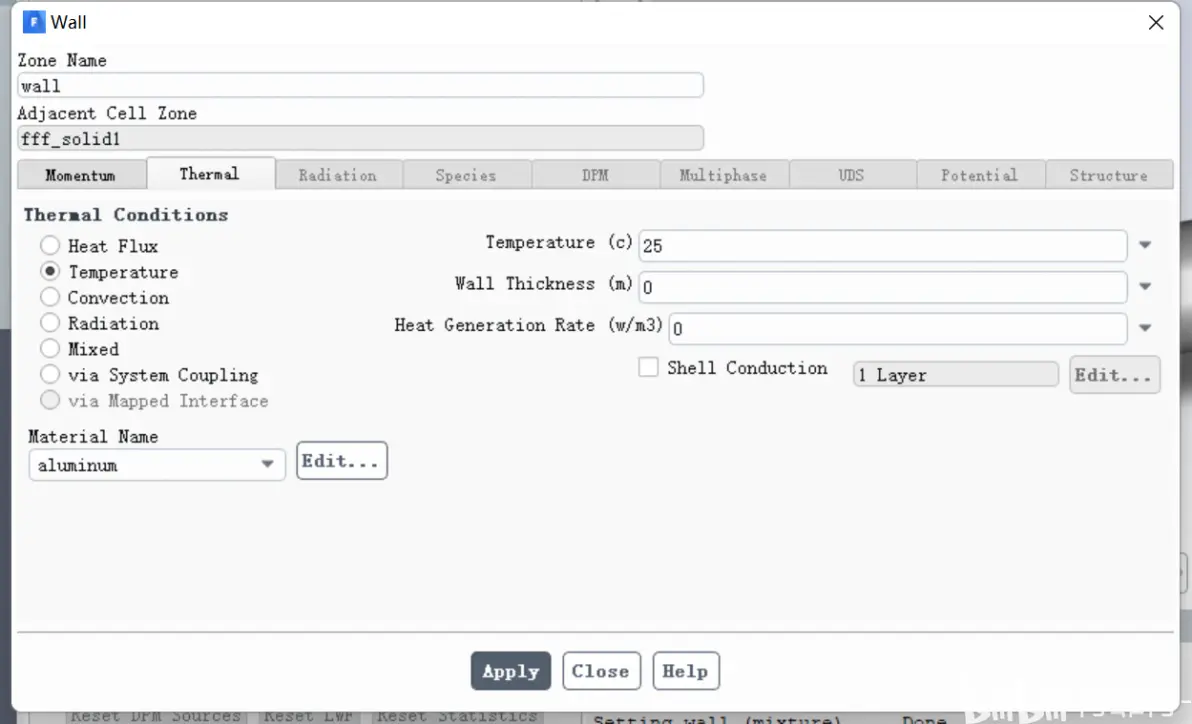
计算完毕后，温度分布如下：

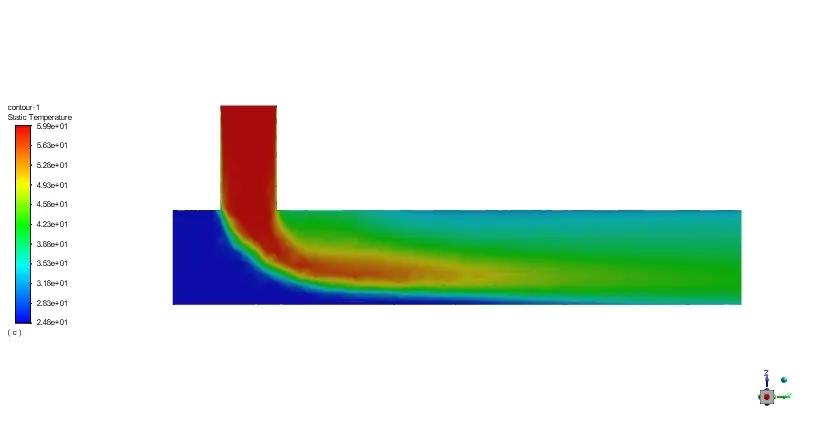
速度分布如下：

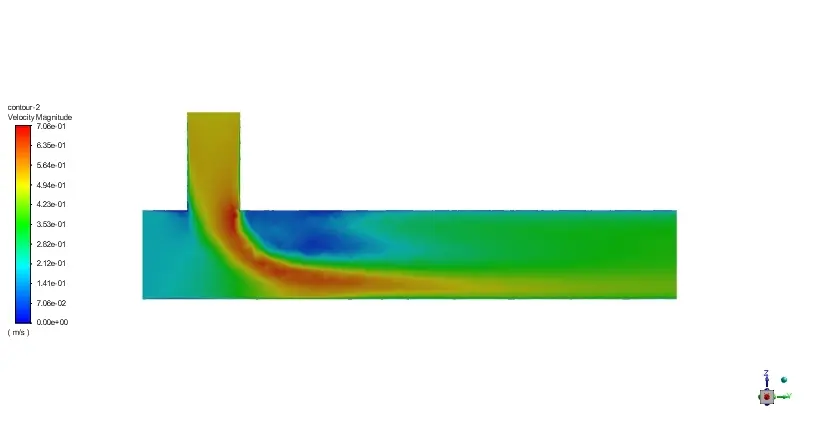
2.共轭传热案例

如下图所示为CPU散热问题计算模型，矩形CPU外部为矩形外流域。

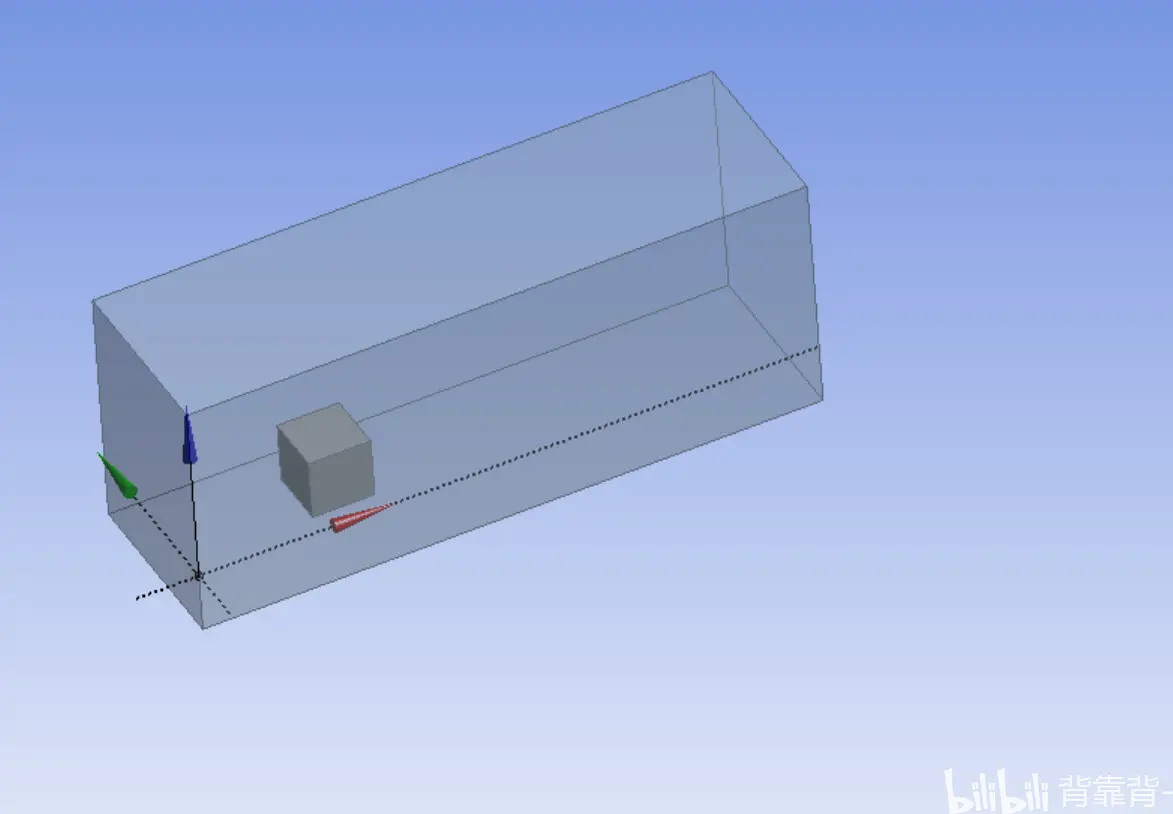
网格如下所示：

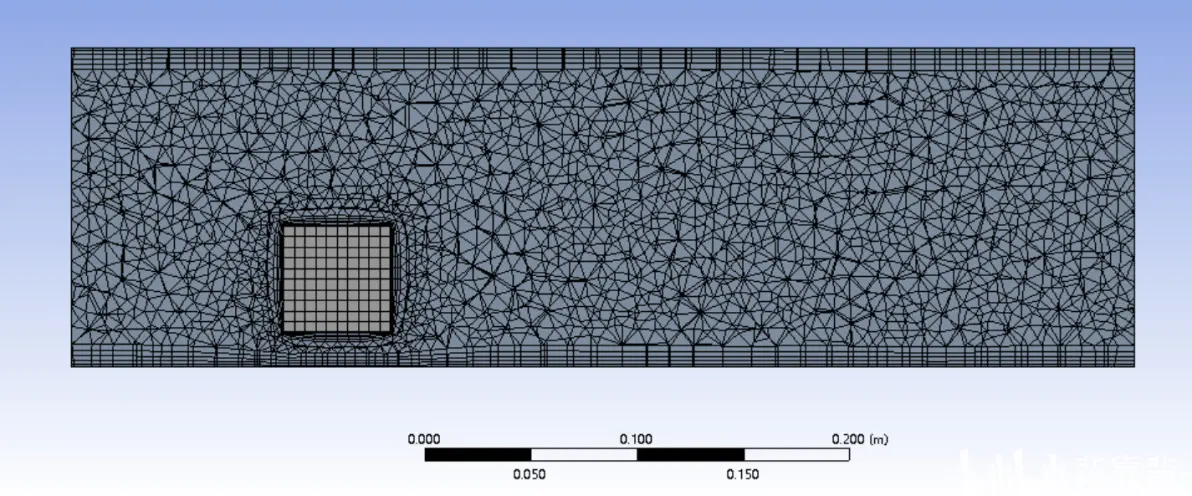
打开Fluent，设置如图，打开能量方程，流体材料为空气，固体材料设置为铜。

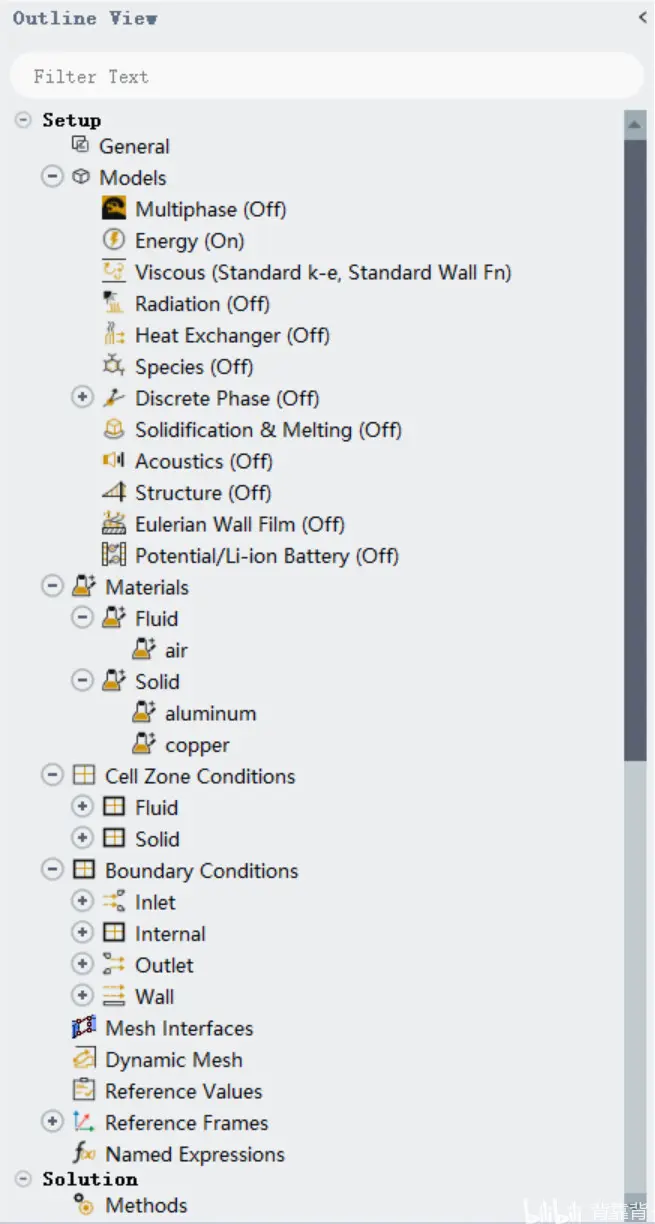
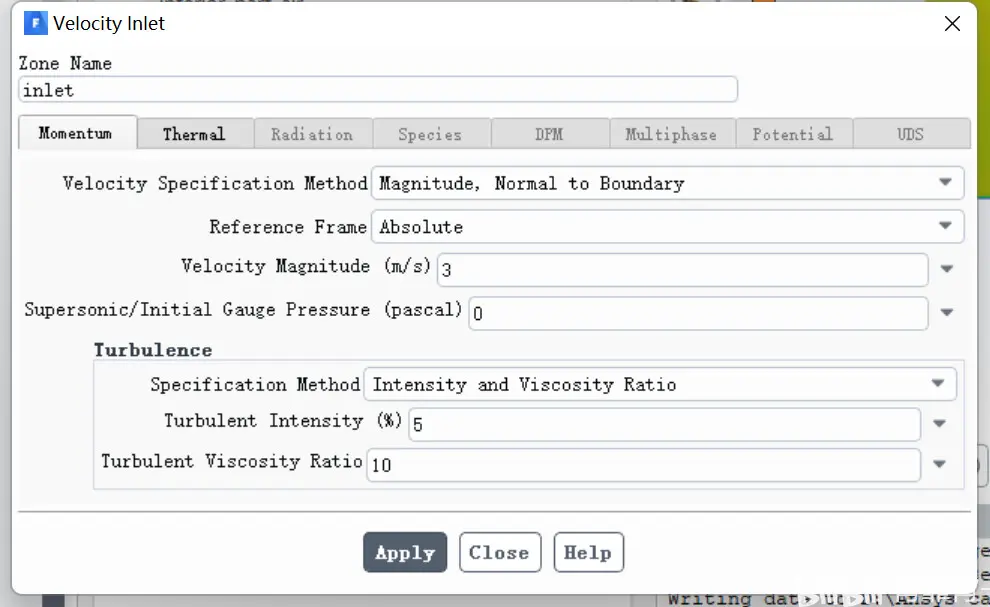
进口给定速度3，温度25度。

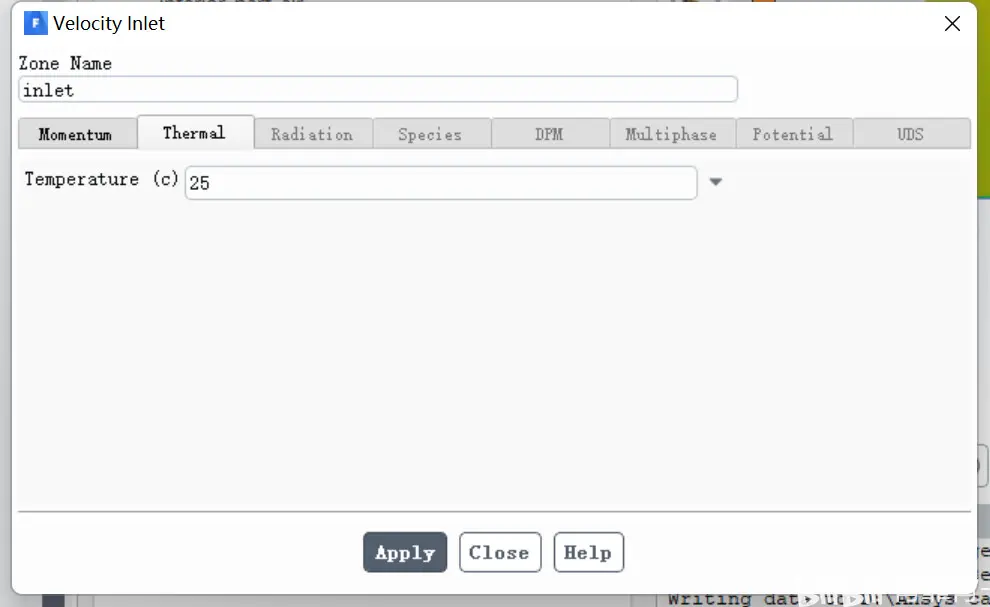
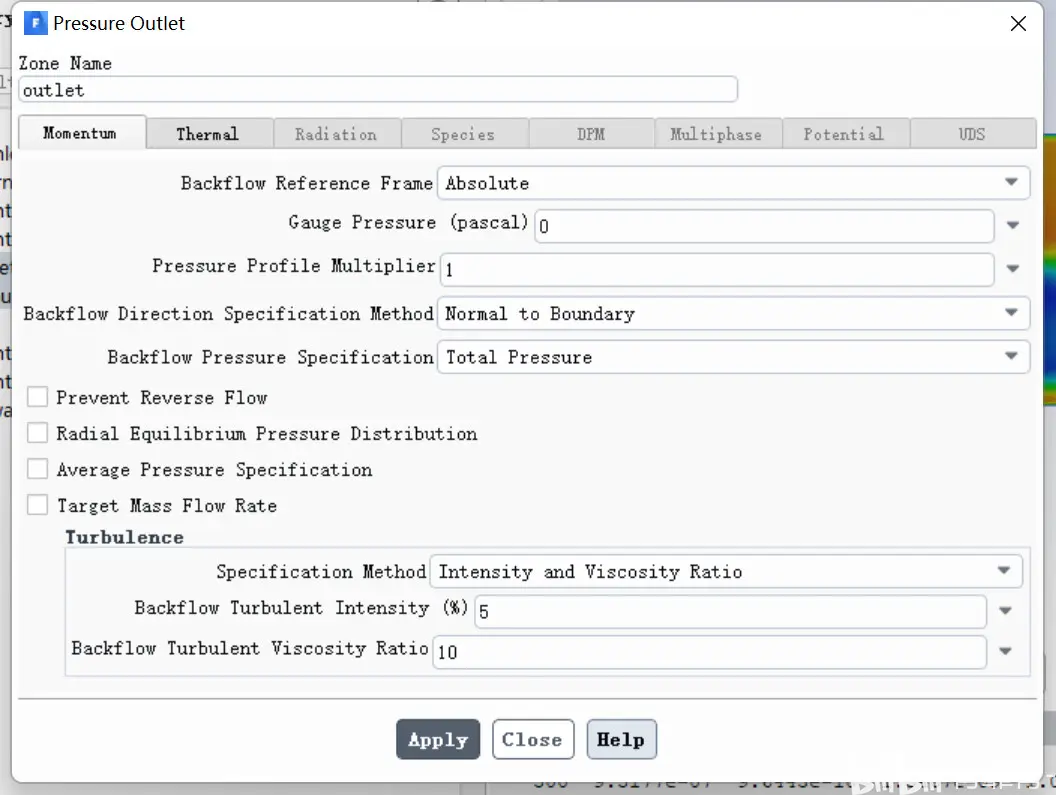
出口设置如下：

壁面设置为：

计算结果如下：

某截面的温度分布为：

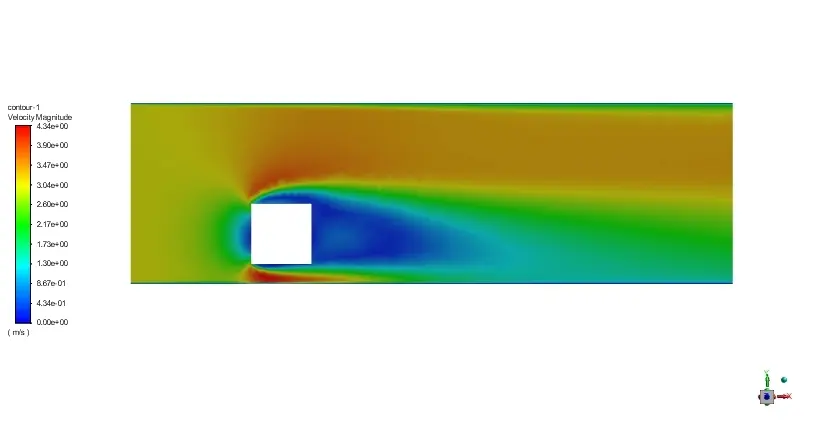
速度分布为：

案例模型文件见评论。

学习原视频为： https://www.bilibili.com/video/BV1mT4y1P7cH/?spm_id_from=333.999.0.0&vd_source=03b97078a665b84af50b20d13a26d2f4