TensorFlow中的激活函数详解

激活函数（Activation Function）运行时激活神经网络中某一部分神经元，将激活信息向后传入下一层的神经网络。

神经网络的数学基础是处处可微的，所以选取激活函数要保证数据输入与输出也是可微的。TensorFlow中提供哪些激活函数的API。

激活函数不会改变数据的维度，也就是输入和输出的维度是相同的。TensorFlow中有如下激活函数：

1. sigmoid 函数

这是传统神经网络中最常用的激活函数之一，公式和函数图像如下：

{\displaystyle S(x)={\frac {1}{1+e^{-x}}}.}

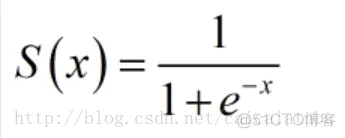
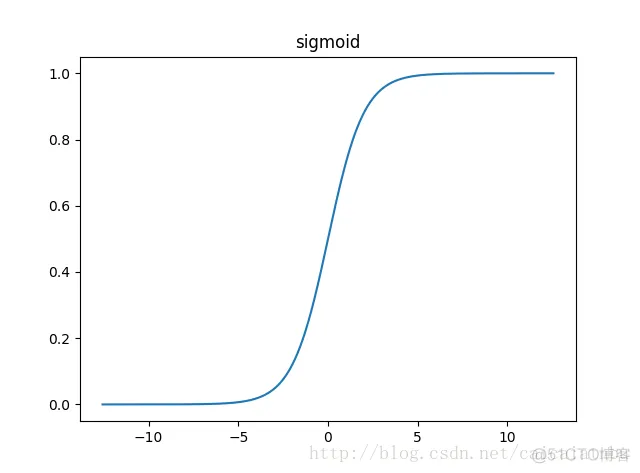
优点：它输出映射在(0,1)内，单调连续，非常适合用作输出层，并且求导比较容易；

缺点：具有软饱和性，一旦输入落入饱和区，一阶导数就变得接近于0，很容易产生梯度消失。

饱和性：当|x|>c时，其中c为某常数，此时一阶导数等于0，通俗的说一阶导数就是上图中的斜率，函数越来越水平。

2. tanh函数

tanh也是传统神经网络中比较常用的激活函数，公式和函数图像如下：

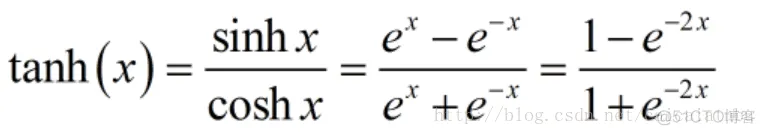
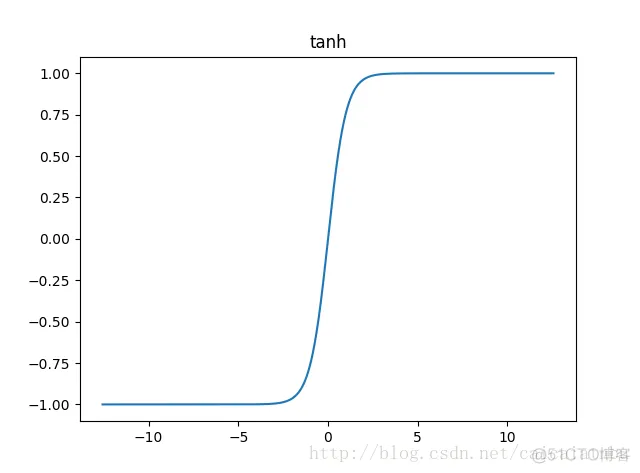
tanh函数也具有软饱和性。因为它的输出是以0为中心，收敛速度比sigmoid函数要快。但是仍然无法解决梯度消失问题。

3. relu 函数

relu函数是目前用的最多也是最受欢迎的激活函数。公式和函数图像如下：

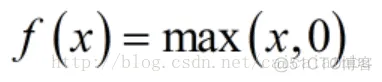
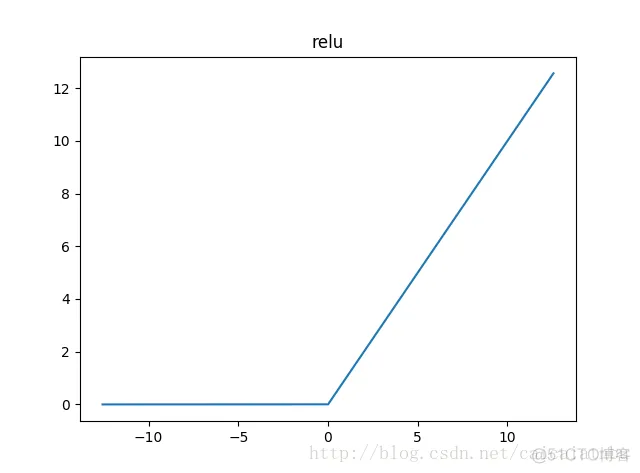
由上图的函数图像可以知道，relu在x<0时是硬饱和。由于当x>0时一阶导数为1。所以，relu函数在x>0时可以保持梯度不衰减，从而缓解梯度消失问题，还可以更快的去收敛。但是，随着训练的进行，部分输入会落到硬饱和区，导致对应的权重无法更新。我们称之为“神经元死亡”。

除了relu本身外，TensorFlow还定义了relu6，也就是定义在min(max(features, 0), 6)的tf.nn.relu6(features, name=None),以及crelu,也就是tf.nn.crelu(features, name=None).

4. softplus 函数

softplus函数可以看作是relu函数的平滑版本，公式和函数图像如下：

5. leakrelu 函数

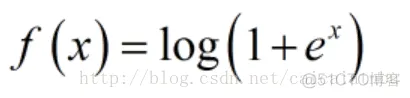
leakrelu函数是relu激活函数的改进版本，解决部分输入会落到硬饱和区，导致对应的权重无法更新的问题。公式和图像如下：

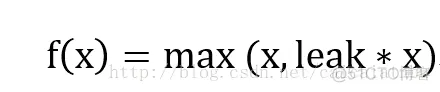
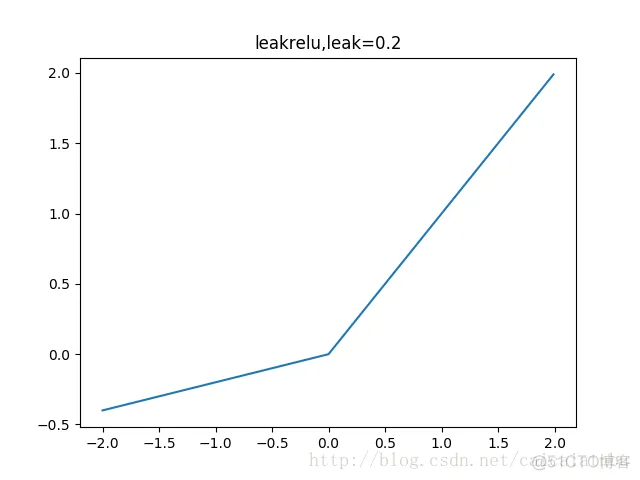
左边缩小方差，右边保持方差；方差整体还是缩小的，而均值得不到保障。

6. ELU 函数

leakrelu函数是relu激活函数的改进版本，解决部分输入会落到硬饱和区，导致对应的权重无法更新的问题。公式和图像如下：

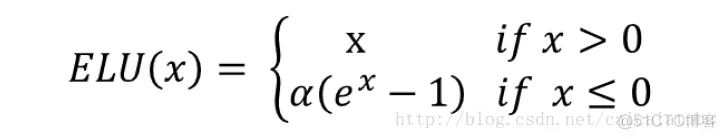
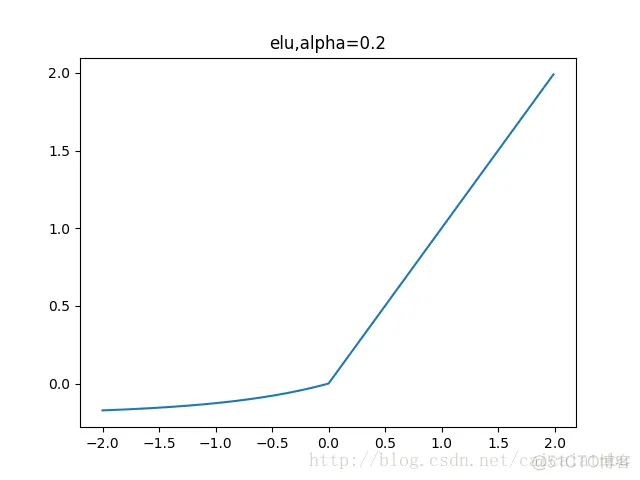
左边缩小方差，右边保持方差；方差整体还是缩小的，而均值得不到保障。

7. SELU函数

最近的自归一化网络中提出，函数和图像如下：

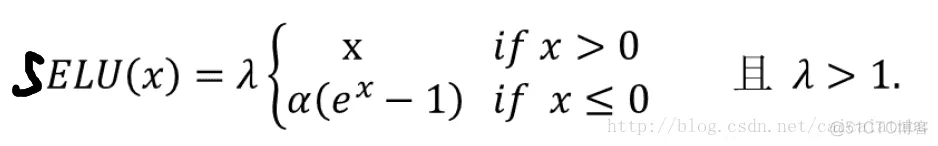
蓝色是：selu，橙色是：elu

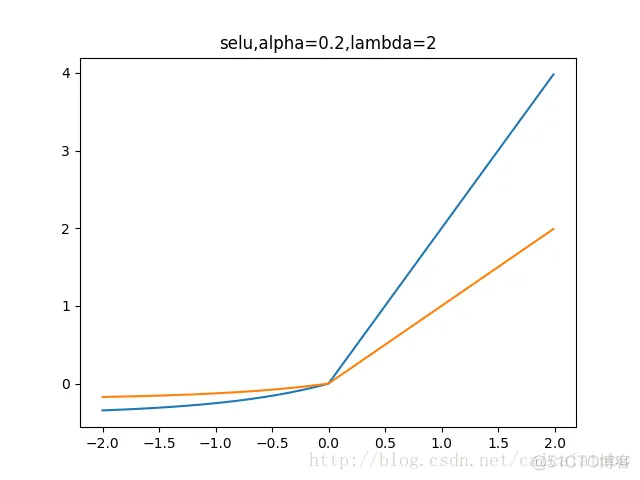
左边缩小方差，右边放大方差，适当选取参数alpha和lambda，使得整体上保持方差与期望。如果选取：

lambda=1.0506，alpha=1.67326，那么可以验证如果输入的x是服从标准正态分布，那么SELU(x)的期望为0，方差为1.

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删