简化版Prony算法参数辨识仿真研究

1.问题描述：

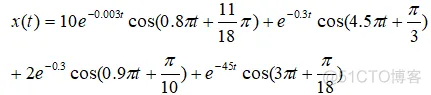
被测信号中包含四个振荡模态，在数据窗宽度同样为10s的前提下，利用不同的采样频率做普罗尼计算。

2.部分程序：
 

登录后复制

function X = func_Prony(Signal,dt);s     = Signal;  
L     = length(s(1:length(Signal)));  Order = ceil(L/2);  
R     = [];  K1    = 0;    K2    = 0; %扩展矩阵  while K1 <= Order      K2  = 1;      
Re = [];      while K2 <= Order          u  = Order - K2 +1;          v  = L - K2;          
m  = Order - K1 +1;          l  = L - K1;          r  = sum(s(u:v).*conj(s(m:l)));          
Re = [Re,r];          K2  = K2 + 1;      end      R = [R,Re'];      K1 = K1 + 1;  
end %计算阶数  Order = func_Order(R); %计算相关参数 K2 = Order-1;  Re = R(2:end,2:K2+1);  
b  = R(:,1);  b  = b(2:end);  a  = pinv(Re)*(-b); R1 = R(1,:);  R1 = R1(1:K2+1);  
a1 = [1 a']; Ep = sum(R1.*a1);  P  = [1 a'];  z  = roots(P); %估计序列X  ks    = 1:K2;  
X(ks) = s(ks); for Order = K2+1 : L      Lij      = 1:K2;      X(Order) = sum(-a'.*s(Order-Lij));      
Order    = Order+1;  end Zh = [];  for mm = 0:L-1      Zh = [Zh,z.^mm];  end Z    = Zh';  Z    = conj(Z);  
Zhh  = Z';  b    = (Zhh*Z)^(-1)*Zhh*X';  %最后得到的四个参数值 A     = abs(b) f     = angle(z)/2/pi/0.001 a     
= log(abs(z))/dt theta = angle(b)/2/pi/dt1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25
.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.

3.仿真结论：

注意，这里论文中你所给的那个公式，貌似有点小错误，这里我们使用了两组公式进行计算，一组是你所提供的公式，一组是我们给的测试数据。

仿真结果如下所示：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删