HullWhite短期利率模型的R语言仿真分析

Hull and White（1994）模型解决Vasicek模型对利率的初始期限结构的拟合不佳的问题。该模型定义为：

Wt是风险中性框架下的维纳过程，模拟随机市场风险因素。σ是标准差参数，影响利率的波动，波动幅度有着瞬时随机流动的特征。参数b,a,σ和初始条件r0是完全动态的，并且瞬时变动。

该模型的另一种示形式是：

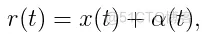
假定a是非负数：

b:长期平均水平。在长期水平下产生一系列r的轨道值。

a:回归速度。代表b的轨道值实时重组的速度。

σ：代表瞬时波动，测量每个时点随机因素进入系统的​ ​振幅​​。

以下是由公式导出的一些数值：

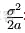:长期方差。计算在长期所有r值围绕平均值重组的轨道值。

a与σ数值相反波动：增加σ会增加随机数进入系统的数量，

当a增加会使方差稳定，围绕长期平均值b以方差值波动。这在看长期方差时十分明显。 当方差值不变时，若σ增加,a减少。此模型是一个奥恩斯坦 - 乌伦贝克随机过程。

这些假设以及 对信贷/流动性风险的简单（并行）调整仍在保险中广泛使用 ，但在2007年次贷危机后被市场抛弃。

有关新的多曲线方法的更多详细信息，请参见例如 ​ ​http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2219548​​。在本文中，作者介绍了一个多曲线自举(bootstrap)过程。

＃清理工作区

登录后复制

rm(list=ls())1.

＃模拟的频率

1. freq <- "monthly"
2.  
3. delta_t <- 1/12

＃数据

1. params <- list(tradeDate=as.Date('2002-2-15'),
2.  
3.                settleDate=as.Date('2002-2-19'),
4.  
5.                payFixed=TRUE,
6.  
7.                dt=delta_t,
8.  
9.                strike=.06,
10.  
11.                method="HWAnalytic",
12.  
13.                interpWhat="zero",
14.  
15.                interpHow= "spline")

＃构建利率期限结构的市场数据

＃存款和掉期

1. tsQuotes <- list(d1w =0.0382,
2.  
3.  
4.                  s2y = 0.037125,
5.  
6.                  s3y =0.0398,

＃具有相应期限和期限的掉期波动率矩阵

1. swaptionMaturities <- c(1:5)
2.  
3. swapTenors <- c(1:5)
4.  

＃为掉期定价

登录后复制

pric <- Swaption(params, swaptionMaturities, swapTenors,1.

＃构建利率的即期期限结构

＃根据输入的市场数据

1. times <- seq(from = delta_t, to = 5, by = delta_t)
2.  
3.  
4. maturities <- curves$times
5.  

############## Hull-White短期利率模拟

＃模拟次数，频率

1. horizon <- 5
2. sims <- 10000

＃校准Hull-White参数

1. a <- pricing$a
2.  
3. sigma <- pricing$sigma

＃使用模拟高斯冲击

登录后复制

simshos(n = nb.sims, horizon = horizon )1.

＃使用模拟因子x

＃我使用远期汇率。由于每月的频率较低，

＃我认为它们是瞬时远期汇率

1. fwdrates <- ts(replicate(nb.sims, curves$forwards),
2.  
3.                 start = start(x),
4.  
5.                 deltat = deltat(x))

＃ α

1.  
2.  
3. alpha <- fwdrates + param.alpha

＃短期利率

登录后复制

r <- x + alpha1.

＃随机贴现因子（当前的数值积分是非常基本的）

＃由随机贴现因子得出的蒙特卡洛价格和零利率

1.  
2. montecarlozerorates <- -log(montecarloprices)/maturities

＃市场和蒙特卡洛价格之间的差异的置信区间

1. conf.int <- t(apply((Dt - marketprices)[-1, ], 1, function(x) t.test(x)$conf.int))
2.  
3.  

1. par(mfrow = c(2, 2))
2.  

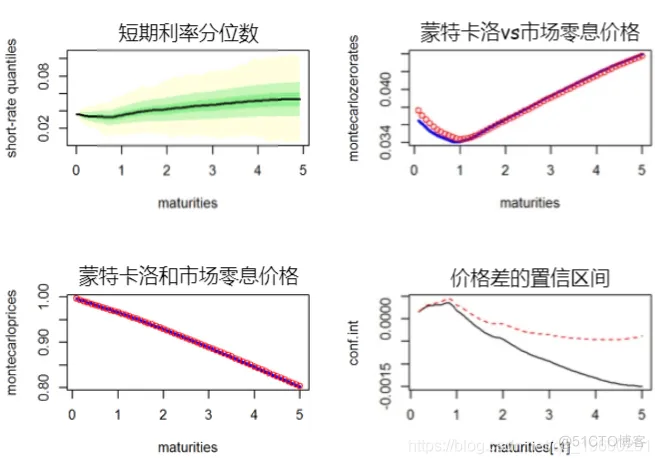
＃短期利率分位数

＃蒙特卡洛vs市场零利率

1. plot(maturities, montecarlozerorates, type='l', col = 'blue', lwd = 3,
2.  
3. points(maturities, marketzerorates, col = 'red')

＃蒙特卡洛vs市场零息价格

1. plot(maturities, montecarloprices, type ='l', col = 'blue', lwd = 3,
2.  
3. points(maturities, marketprices, col = 'red')

＃价格差的置信区间

登录后复制

matplot(maturities[-1], conf.int, type = 'l'1.

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删