调制解调原理深度剖析

调制与解调是通讯中非常常见的技术，其实在微弱信号采集中也会用到此技术，那么调制与解调究竟是怎么一回事呢？

1.    让我们先建立直观应用概念，以调幅调制为例，理解调制解调的作用结果，然后再来从原理进行分析。

例1：微弱信号放大。

假如当前有一信号X = sin(2πt)+ 1；其包含了一个1V的直流成分，时域、频域波形见下图。

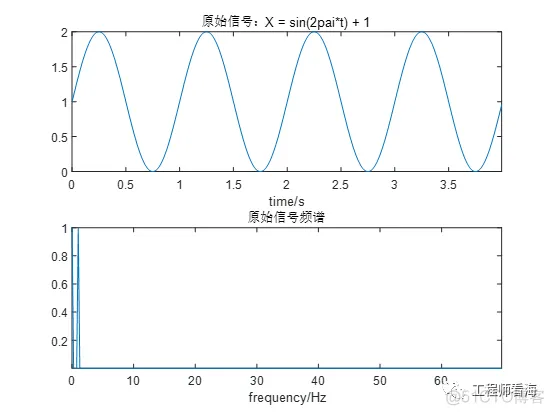
如果想去直接放大原始信号，那么它包含的直流信号也会被直接放大，后续电路可能主要处理放大后的直流，甚至会进入非线性区域，影响后续电路正常工作。

我们可以加一个隔直电容，或高通电路，来抑制这个直流，然后在进行交流放大，然而这个缺点是对于有一定带宽的信号，在去除直流成分的同时，也去除了一部分有用的低频信号，伤敌1000自损800，这是我们不希望看到的。

调制与解调为此给出了一种解决方案，其思路是用一个高频信号去调制我们采集的原始信号，把原始信号的频谱搬移到高频去，经过AC放大后，再把频谱搬移回去，实现放大的目的，一箭双雕。

现在我们用一个高频信号去调制原始信号，其过程就是用频率为Fc的高频信号Xc去乘原始信号X，这个高频Fc的频率要远大于原始信号的频率。

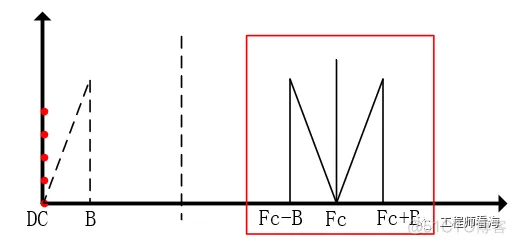
从下图可以看出，调制后的信号以Fc为载波，频谱被搬移到了高频，我们此时可以对其进行放大。如果电路里又引入低频干扰，此时就可以用隔直电容，因为此时低频直流与目标信号频带（Fc±B）已经分离，对引入的直流隔直，就不会造成影响。

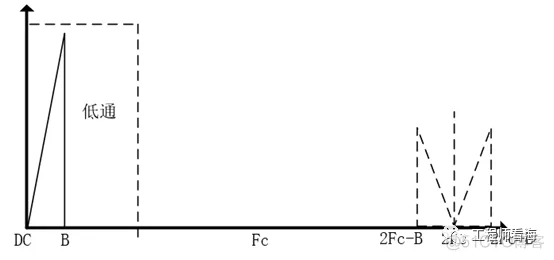
经过调制->AC放大->隔直后的信号，再经过解调，也就是再次频谱搬移后，就又回到原始的频带，虽然增加了（2Fc±B）的成分，只要对其进行低通滤波去除新增的高频部分，就可以实现放大的初衷了。

2.    原理解析。

设目标信号为X = cos(2πB*t)，其频率为B，调制信号Xc=cos(2πFc*t)，其频率为Fc。

二者调制后

Vm = X*Xc = cos(2πB*t)*cos(2πFc*t) = 0.5cos(2π(Fc+B)t)+ 0.5cos(2π(Fc-B)t)，(高中知识哦，不要说以前的知识没用哦)，我们观察Vm中信号的频带是Fc+B与Fc-B。

对Vm进行A倍AC放大后，就可以用隔直电容或高通滤除低频部分。然后再对Vm进行解调，即再乘下调制信号Xc，得到输出Vo，解调过程为:

Vo = Vm * Xc = A*[0.5cos(2π(Fc+B)t) + 0.5cos(2π(Fc-B)t) ] * cos(2πFc*t) = 0.25A[cos(2π(2Fc+B)t) + cos(2π(2Fc-B)t) + 2cos(2πB*t)]

Vo包含了高频也包含了原始频带，对其进行低通后，就可以得到放大后的信号啦。

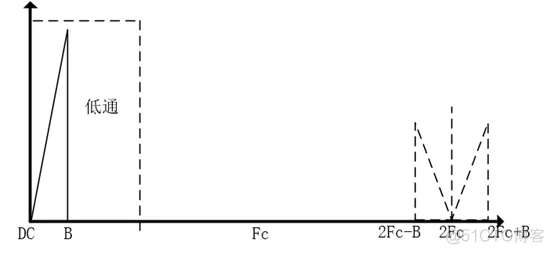
总结调制与解调过程如下：

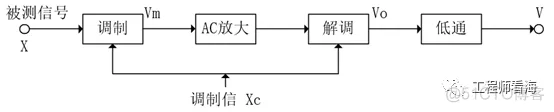
3.    Matlab 仿真

仿真原始信号是(AC1V+DC1V)&1Hz的交流信号

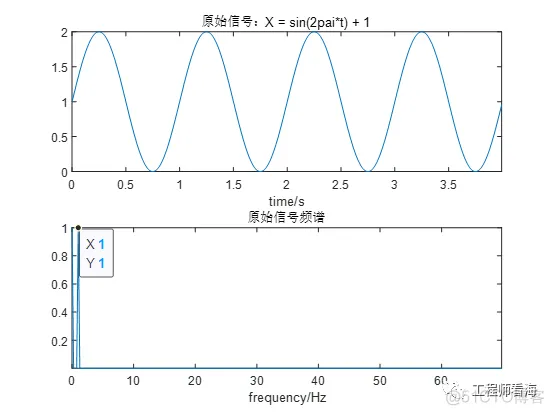
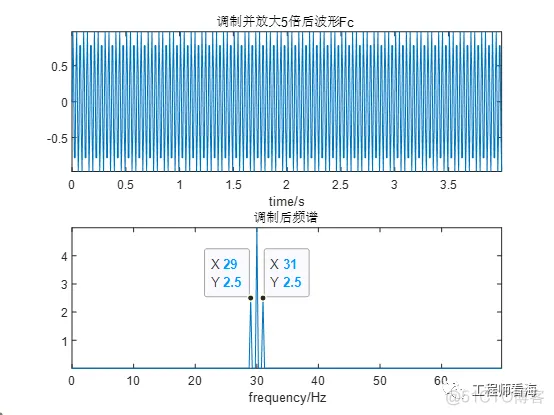
用频率为30Hz的载波调至后，频率被搬移到30Hz±1Hz的位置了，对其进行5倍放大，调制并放大后的时域波形看，其幅值比原始信号要小。

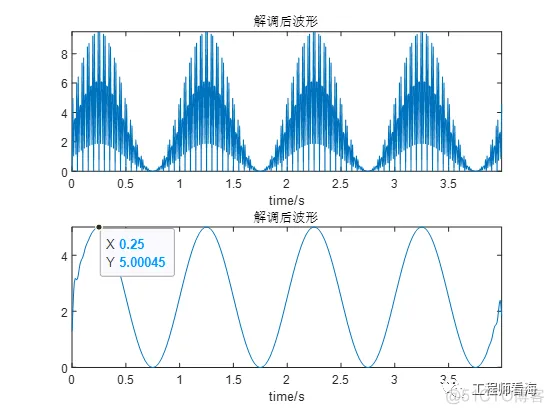
然后对信号解调，再次频谱搬移。原始(AC1V+DC1V)&1Hz的信号，在低频处变为1Hz&(0.25*5*2)=2.5V，与前文理论分析结果一致。

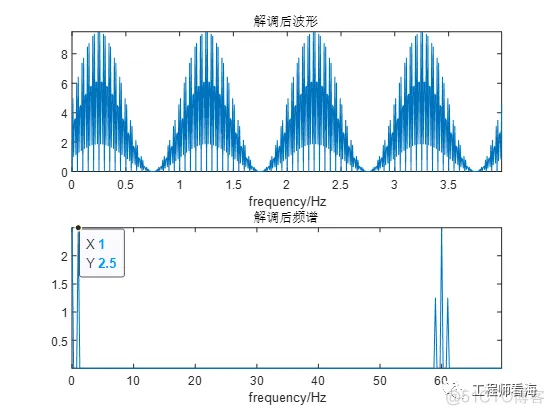
经过低通滤波后的波形如下：

以上就是调制解调的原理介绍，感谢点赞享，让知识变得更简单。

---The end---

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删