图像多重分形谱的MATLAB仿真计算

1.算法仿真效果

matlab2022a仿真结果如下：

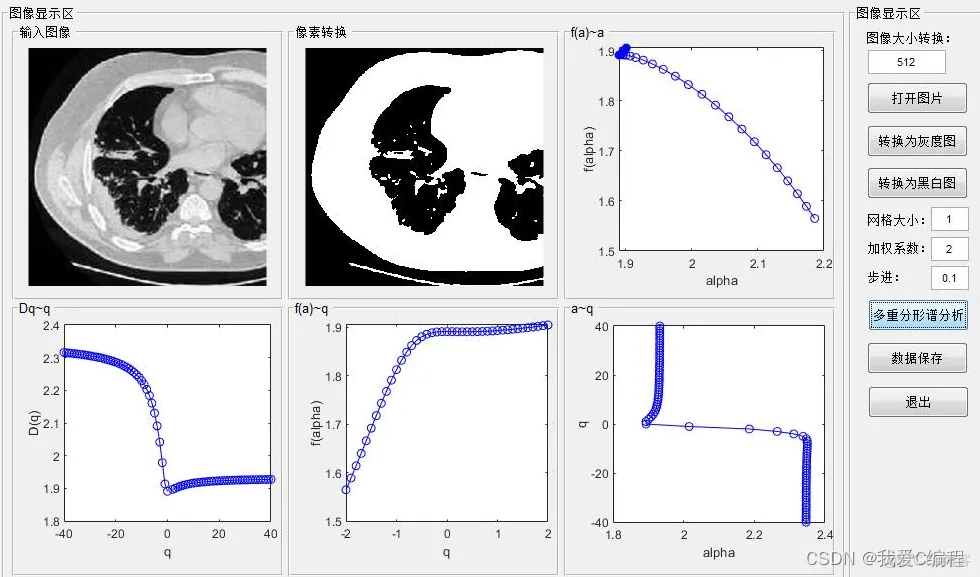
2.算法涉及理论知识概要

多重分形(multifractal)一种分为多个区域的复杂分形结构。为了对分形的复杂性和不均匀性进行更细致地刻画，需引进它的概率分布函数及其各阶矩的计算，由此构成了分形维数的一个连续谱，称之为多重分形或多标度分形。

由于多重分形至今尚无严格的数学定义，以下仅通过实例进行简单的描述.设有一个分布不均匀的分形，首先将它分成若干个小区域，定义第i区域内的密度分布函数为尸，假定尸，存在着标度关系.其中e是一个小的测量单位，a是一个标度指数，称为奇异指数，它是反映分形体内各个小区间的奇异程度的一个量，所以a的数值与其所在的位置有关.进一步将分形上具有相同a值的小区间数记为

f (a)被称为奇异谱，因为它将奇异值a的密度用一个连续函数来表示.另一方面，还可将分布函数进行加权求和，得到

r(y)常称为质量指数.再定义加权后的广义分形维数D。为

登录后复制

从上述公式中可知，当9=。时，D。就是普通的分形维数，而D,称为信息维数，D:称为关联维数.因此，几，被称为广义分形维数.经过简单的计算可得a, 六a)和:<q) }D、这两组参量之间的对应关系式为.

这一系列公式给出了多重分形理论的基本核心.利用多重分形，可把一个复杂的分形分成许多具有不同奇异程度的小区域来研究，从而能分层次地来 [1]  了解分形的内部精细结构.

   计算多重分形谱概率的方法有两种：一种是针对灰度图像的算法，将图像灰度信息转换为高度矩阵，然后分割求高度概率；另一种是针对黑白图像的算法，分割求白色像素概率（黑色为背景）。

具体计算过程：

计算图像尺寸，L×L，尺寸大小应为L=2^n

对图像进行网格划分，每个网格尺寸为s×s，ε=s/L，1<=s<L，s为能被2整除的正整数

一、首先定义配分函数，此函数是对概率的加权求和，即

三、质量指数。配分函数与尺度ε存在幂函数关系Iq(ε)= ετ(q)，两边取对数，则可得到

3.MATLAB核心程序

登录后复制

for kj=1:p
    count    = 0;
    No_boxes = power(Rs,2)/power(power(2,kj),2);
    for q = -Qran:10*qstep:Qran       
        qsum = 0;
        for i=1:No_boxes
            if PsL(i,kj) ~= 0
               qsum = qsum + power(PsL(i,kj),q);
            end
        end
        fqnum  = 0;
        aqnum  = 0;
        smuiqL = 0;
        for i=1:No_boxes
            if PsL(i,kj) ~= 0
               muiqL = power(PsL(i,kj),q)/qsum;
               fqnum = fqnum + (muiqL * log(muiqL));
               aqnum = aqnum + (muiqL * log(PsL(i,kj)));
               smuiqL = smuiqL + muiqL;
            end 
        end
        count         = count + 1;
        fql(kj,count) = fqnum;
        aql(kj,count) = aqnum;
        qval(count)   = q;
    end
end
for i=1:count
    line   = polyfit(logl,aql(:,i),1);
    aq(i)  = line(1);
    yfit   = polyval(line,logl);
    sse    = sum(power(aql(:,i)-yfit,2));
    sst    = sum(power(aql(:,i)-mean(aql(:,i)),2));
    ar2(i) = 1-(sse/sst);
end
for i=1:count
     line   = polyfit(logl,fql(:,i),1);
     fq(i)  = line(1);
     yfit   = polyval(line,logl);
     sse    = sum(power(fql(:,i)-yfit,2));
     sst    = sum(power(fql(:,i)-mean(fql(:,i)),2));
     fr2(i) = 1-(sse/sst);
end
for i=1:count
    Dq(i) = (aq(i)*qval(i)-fq(i))/(qval(i)-1);
end
 
aqs   = aq;
fqs   = fq;
qvals = qval;
Dqs   = Dq;

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删