利用Matlab进行业务数据深度分析

设个观测值构成行向量

其中是样本容量。它是来自某总体的样本，数值从小到大重新排列为：

这就是次序统计量，显然，最小次序统计量与最大次序统计量分别为：

1 中位数

1.1 样本均值

中位数的计算公式为：

中位数是描述数据中心位置的数字特征，大体上比中位数大或小的数据个数为整个数据个数的一半。对于对称分布的数据，均值与中位数较接近，对于偏态分布的数据，均值与中位数不同。中位数的另一显著特点是不受个别极端数据变化的影响，具有较好的稳定性。

1.2 MATLAB编程-中位数

计算中位数使用的是函数median

xmed=median(x);

也可以使用函数prctile,计算分位数，第二个参数为50。

x50=prctile(x,50);

代码中x50和xmed都表示中位数，只是使用函数不同，书写不同以示区分。

2 分位数

2.1 上四分位数、下四分位数、四分位极差、三均值、上截断点、下截断点

对和容量为的样本，它的分位数（又叫100百分数）为：

其中表示的整数部分，当时，定义。大体上整个样本的的观测值不超过分位数。0.5分位数（第50百分位数）就是中位数。实际应用中，0.75分位数和0.25分位数比较重要，分别记作上、下四分位数，记作：

上、下四分位数之差称为四分位极差（或半极差），表示为：

它也是度量样本分散性的重要数字特征，尤其对于具有异常值的数据，它作为分散性的度量具有稳健性，因此它在稳健型数据分析中具有重要作用。

当样本是来自正态总体时，其总体上、下四分位数为：

故其总体四分位极差为：

也即：

当样本存在异常值时，标准差缺乏稳健性。根据上面的讨论，可以得到总体标准差的一个具有稳健性的估计：

它称为四分位标准差。对于任意观测数据，可以作为数据分散性的稳健度量。

我们知道，均值和中位数都是描述数据集中位置的数字特征。计算时，用了样本的全部信息，而只是用了数据分布中的部分信息，因此在正常情况下，用比用描述数据的集中位置更优，但当数据存在异常值，缺乏稳健性，这时可用三均值作为数据集中位置的数字特征。三均值的计算公式为：

在探索性数据分析中，有一种判断数据为异常值的简便方法。称和为数据的下、上截断点。大于上截断点的数据为特大值，小于下截断点的数据为特小值，两者都为异常值。

当总体为正态分布时，理论上、下截断点分别为：

数据落在上、下截断点之外的概率为0.00698，即对于容量较大的样本，其异常值的概率约为0.00698，由模拟研究，对容量为的正态样本，异常值的平均比率近似为0.00698+。

2.2 MATLAB编程-上四分位数、下四分位数、四分位极差、三均值、上截断点、下截断点

计算上四分位数和下四分位数用的是函数prctile,函数的第二个参数分别为75和25。

x75=prctile(x,75);%上四分位数
x25=prctile(x,25);%下四分位数

计算四分位极差根据定义来，利用上面得到的上四分位数和下四分位数：

xr1=x75-x25;%四分位极差

计算三均值根据定义计算：

xhM=0.25*x25+0.5*x50+0.25*x75;%三均值

计算上截断点和下截断点根据定义计算:

xsj=x75+1.5*xr1;%上截断点
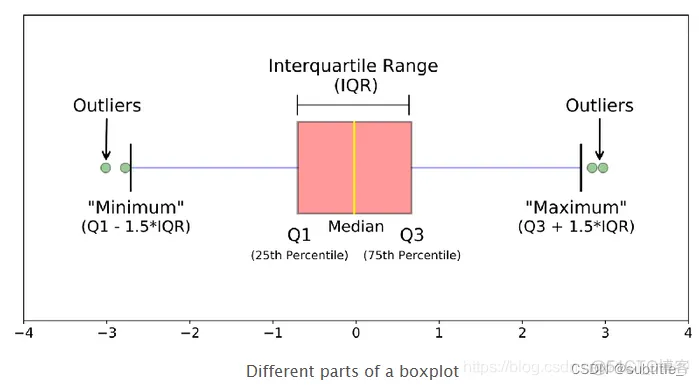
xij=x25-1.5*xr1;%下截断点

最后用一张图说明所有：

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删