只要有先后顺序的序列,都可以称之为“时间序列”(广义上的定义)。因此,科学研究中绝大多数的序列都可以叫做时间序列,而对于时间序列的分析,简称时序分析。
对于一个时间序列,首先要区别其中的一些基本内容,如:采样间隔(采样频率的倒数)、数据点个数N、整个时间跨度T。根据采样间隔的一致性可以分为等间隔数据或不等间隔数据。而基于采样频率的高低可以分为(较)高精度数据、(较)低精度数据等。
无论是等间隔还是不等间隔,都应基于等间隔的推论,因此,对于时间序列自身的采样定理就显得尤为重要(如图一)。

图一. 采样定理
再者,要注意厘清的是无论是什么情况,对于理想的时间序列,肯定都是基于无限长、连续的理想状态,而只要是观测就是有限的,这就是被迫地加上了一种“矩形窗”,就会产生截断效应。然后,因为时间序列是不连续的,经过等距脉冲地“采样”过程,变成了一个离散的等间隔数据序列(后面不做类似赘述)。图一中,Δ相当于时间间隔(采样频率记为Fs=1/Δ)。Δ必须要满足采样定理所约束的条件,否则就会出现频谱混叠。

图二. 频谱混叠和截断效应、常见窗函数的性质
图二中,还提及一些常见窗函数的性质(矩形窗、三角窗、余弦型窗等),这些都是对时间序列进行频谱分析时常常增加的窗函数,默认就是矩形窗。说到这里,不得不先补充一些时间序列的频谱分析内容。
每一个时间序列的分析都有其各自的特点,但也都有共性,基本上均可以表示成多个准周期三角函数的叠加,再叠上趋势和噪声。通常,可以用下式表示:
对于时间序列的频谱分析,通常有:时域分析(自相关法、分段周期叠加法、相位延迟法PDM等)、频域分析(快速傅里叶变换FFT、Lomb-Scargle法等)、时频分析(小波变幻等)。目前,通常用后两种作为实际应用,而用时域分析作为参考依据。由于时序有各自的特点,不能单一地依靠某种频谱分析法得到相关结果,而至少在两种不同的方法中得到印证。在Matlab操作过程中可以见图三:
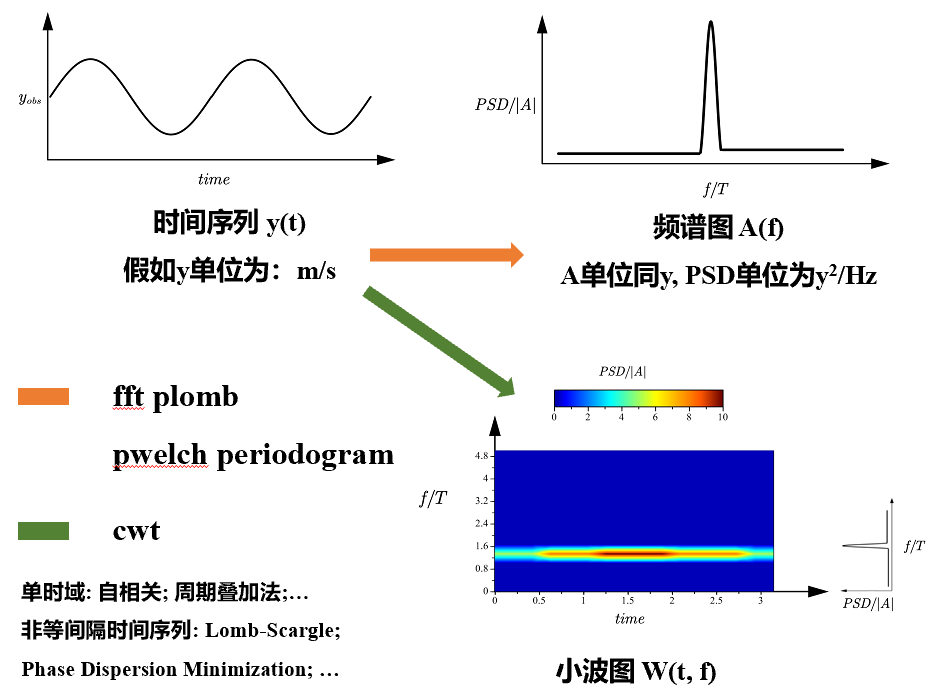
图三. 频谱分析法中Matlab的主要实现函数
在这里,要强调的是,图三中的信号只有唯一一个周期信号,而且信噪比(信号/噪声)明显要搞很多,所以无论是频域还是时频域,都有明显的单峰,对应的频率就是原始信号的周期频率信号或周期。同时,可以看到小波图的右侧其实就可以对应右上的分析结果,这是因为小波共同考虑了时域和频域。
观察到细节的朋友们会发现,这里好像还有好几种坐标表达形式,一是A(振幅谱)、二是PSD(功率谱密度),这些又是怎么进行转化的呢?(见图4)
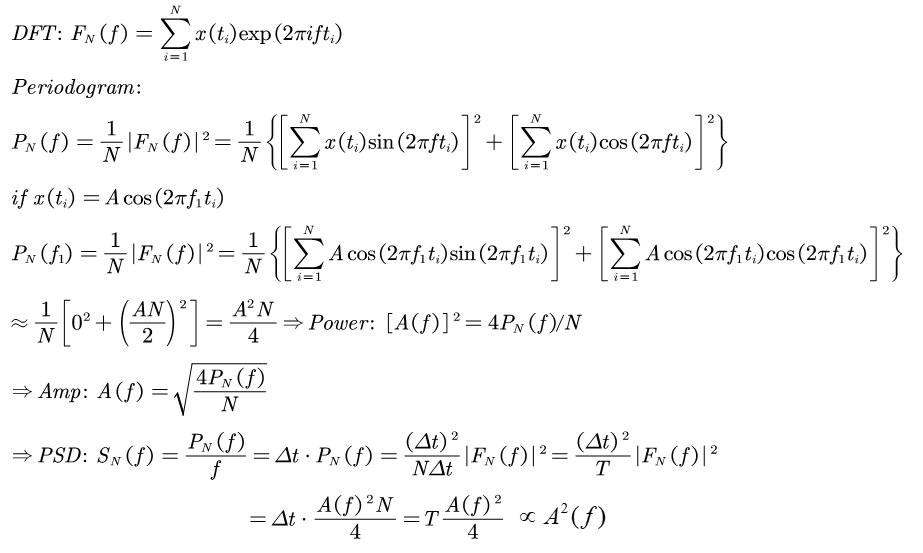
图四. 摘录自C. Aerts, J. Christensen-Dalsgaard, D. W. Kurtz
(2010, Chapter 5, page 354)
所以在Matlab中调用对应方法的函数时,一定要注意最后计算的结果是哪种谱:振幅谱Amp、功率谱Power、功率谱密度PSD。Matlab给出的函数调用指南中,经常也会忽视这一种,用一种Magnitude(dB)的单位,这可不能直接拿来用,因为你得了解它到底是怎么转化的(如图五)。

图五. Matlab中单位的区别
在掌握了这些背景知识后,方能再去对对应的时间序列“对症下药”,不过还是要多多尝试各种方法,有时候“肉眼”观察也是必不可少的环节。对于具体函数的调用,和后续的一些时序处理,将在之后的时序篇继续进行较为细致的表述。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删