MATLAB中的PCA分析方法

pca( )

采用matlab自带的函数pca()进行主成分分析

[coeff, score, latent, tsquared, explained, mu] = pca(x)

假设数据x为n行p列的多变量数据，n为观测次数，p为变量维度。

coeff：为PCA变换系数，也称为loadings。

score：为PCA变换后的主成分（潜变量）。

latent：这里指的是各个主成分解释的方差。

tsquared：Hotelling's T-squared统计量（等价于潜变量的马氏平方距离，即mahal(score,score)）

explained：指的是每个主成分解释的方差所占百分比。

mu：x中每列（每个变量）的均值。

示例

假设x具有6个变量。

coeff

coeff =

0.3523 -0.1291 0.2885 0.1351 0.6760 -0.5483
   0.3405    0.5773    0.6790   -0.0005   -0.2867    0.0865
   0.2557   -0.2643    0.1687   -0.0672    0.4160    0.8116
   0.4491   -0.3097   -0.1197    0.7441   -0.3653    0.0314
   0.5791    0.4562   -0.6329   -0.2062    0.1145    0.0220
   0.3969   -0.5255    0.1114   -0.6173   -0.3757   -0.1779

latent =

0.0024
   0.0003
   0.0002
   0.0001
   0.0000
   0.0000

explained =

80.4144
10.1631
5.5321
2.2133
1.2835
0.3936

mu =

0.0469 0.0407 0.0355 0.0596 0.0614 0.0486

（1）检查主成分score

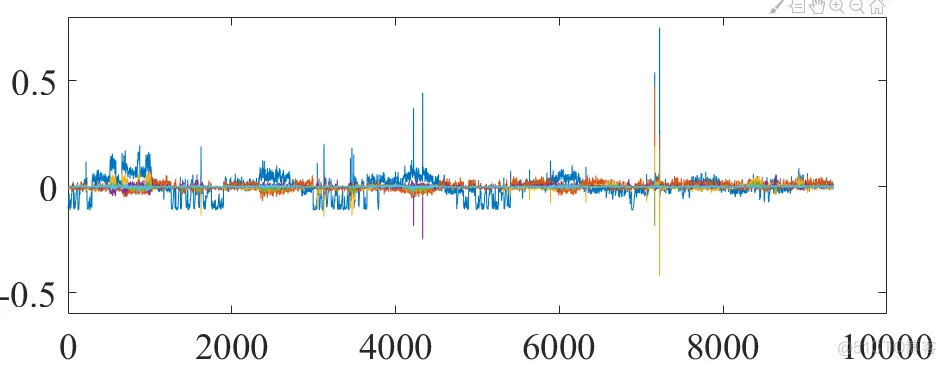
图1 各主成分的分布

(2) 重构

% 重构（减去均值后的数据）
Xcentered = score*coeff'; 

注意pca系数要转置，重构结果是x减去均值mu后的值。

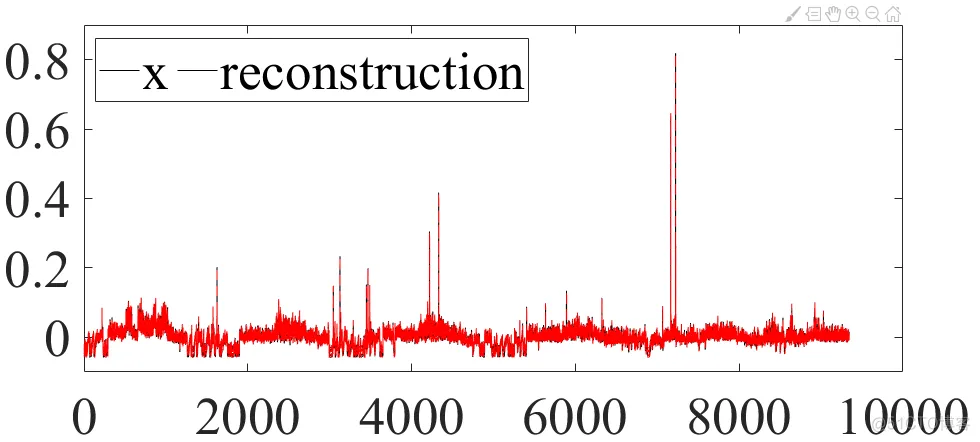
图2 重构结果

(3)  仅保留前n个主成分

% 仅取前n个主成分（T2依然是6个主成分的值）
NumComponents = 1;
[coeff,score,latent,tsquared,explained,mu] = pca(RL2_mean, 'NumComponents', NumComponents);

注意返回的T2依然是6个主成分的值。

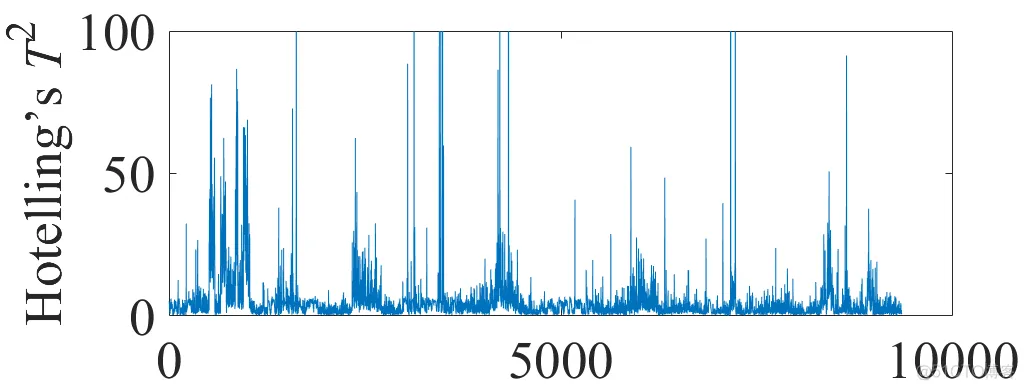
图3 T2统计量

可以计算保留的主成分空间和残差主成分空间的T2统计量

% 保留主成分空间的T2（其实就是马氏平方距离）
tsqreduced = mahal(score,score);
% 残差主成分空间的T2
tsqdiscarded = tsquared - tsqreduced;

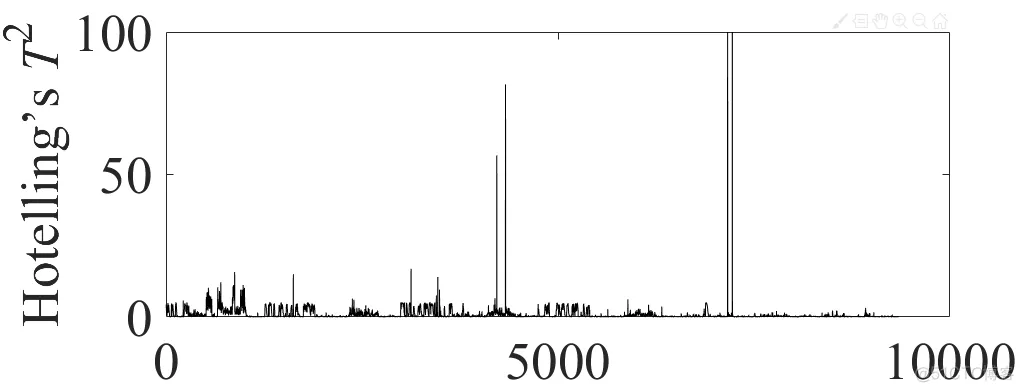
图4 主成分空间T2统计量

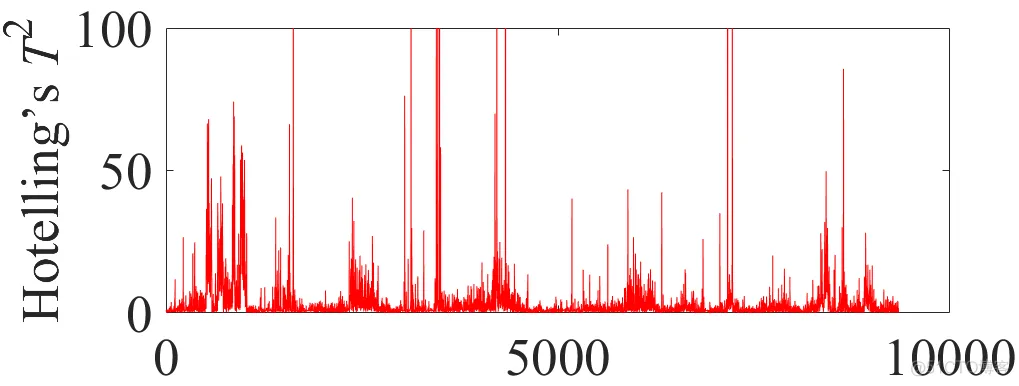
图5 残差主成分空间T2统计量

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删