产品
状态方程模型
1、 状态方程形式1：Linear Polynomial
这个多项式状态方程，单位初始体积的内能呈线性，E由
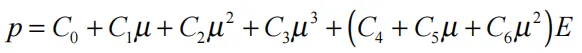（17.1.1）
其中C0，C1，C2，C3，C4，C5和C6是用户定义常数。
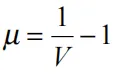（17.1.2）
V是相对体积，在膨胀单元中，的系数设为零，即：
线性多项式状态方程可用伽马定律状态方程来模拟气体。这可以通过设置来实现：
和
其中是比热的比率。压力则由下式给出：
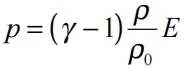
请注意，E的单位是压力的单位
2、 状态方程形式2：JWL High Explosive
JWL状态方程将压力定义为相对体积，V，以及单位初始体积的内能，E，的函数：
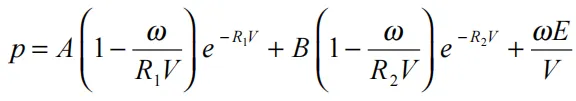（17.2.1）
其中，ω、A、B、R1和R2为用户定义的输入参数。这个状态方程通常用于在涉及金属加速度的应用中确定烈性炸药的爆轰产物的压力。该方程的输入参数由Dobratz [1981]给出了各种高爆炸材料的输入参数，该状态方程与爆炸燃烧（材料模型8）材料模型一起使用，该模型决定了爆炸单元的点火时间。
3、 状态公式形式3：Sack “Tuesday” High Explosives
爆轰产物的压力根据相对体积V和单位初始体积的内能E给出，如[Woodruff 1973]：
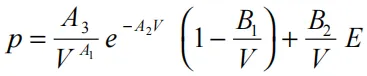（17.3.1）
其中A1、A2、A3、B1、B2为用户定义的输入参数
该状态方程与爆炸燃烧（材料模型8）材料模型一起使用，该模型决定了爆炸单元的点火时间。
4、 状态方程形式4：Gruneisen
具有立方激波速度-粒子速度的Gruneisen状态方程将压缩材料的压力定义为
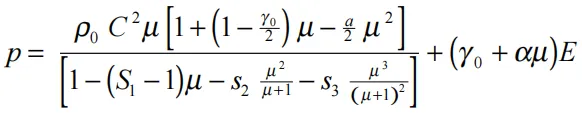（17.4.1）
其中E为单位初始体积的内能，C为vs—vp（剪切-压缩波速）曲线的截距，S1、S2、S3为vs—vp曲线的斜率系数，γ0为Gruneisen gamma，a为对γ0的一阶体积修正。常数C、S1、S2、S3、γ0、a均为输入参数。压缩根据相对体积V定义为：
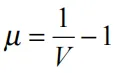
对于膨胀材料，其压力的定义为：
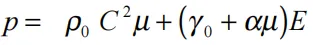（17.4.2）
5、 状态方程形式5：Ratio of Polynomials
多项式状态方程比率将压力定义为：
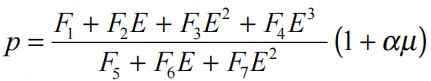（17.5.1）
其中
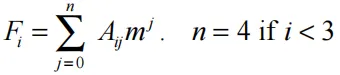（17.5.2）
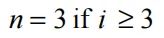
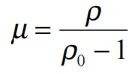
在扩展区域中，F1被F’1=F1+βµ2替代，常数Aij，α和β是用户输入。
6、 状态方程形式6：Linear With Energy Deposition
这个多项式状态方程，单位初始体积，E，的内能呈线性，由
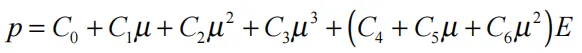（17.6.1）
其中C0，C1，C2，C3，C4，C5和C6是用户定义常数。
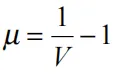（17.6.2）
V是相对体积，在膨胀单元中，的系数设为零，即：
内能E根据能量沉积速率随时间曲线的增加，其ID在输入中定义。
7、状态方程形式7：Ignition and Growth Model
JWL状态方程将未反应高爆物的压力定义为
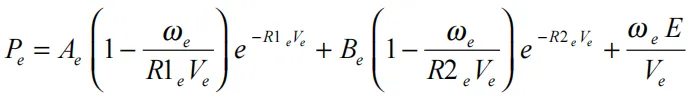（17.7.1）
其中Ve为相对体积，Ee为内能，常数Ae、Be、ωe、R1e、R2e为输入常数。同样地，反应产物中的压力也由另一种JWL形式来定义
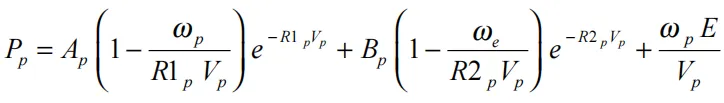（17.7.2）
未反应的炸药和反应产物的混合物由反应的分数F定义（F = 0表示没有反应，F = 1表示从炸药完全转化为产物）。假设压力和温度处于平衡状态，并假设相对体积为添加剂：
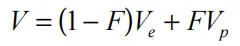（17.7.3）
反应的速率被定义为
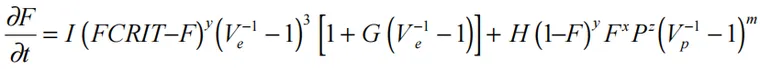（17.7.4）
其中，I、G、H、x、y、z和m（通常是m = 0）是输入常数。
对PBX-9404、RX-03-BB、PETN和铸造TNT四种炸药的JWL状态方程和反应速率拟合了一维和二维冲击起始和爆炸数据。计算方法的细节由Cochran和Chan [1979]描述。Lee和Tarver [1980]给出了这四种炸药的详细的一维计算和参数。Tarver和Hallquist [1981]讨论了PBX 9404和LX- 17对该模型的二维计算。
8、状态方程形式8：Tabulated Compaction
压缩压力为正，容积应变εV为正。表格压缩模型与单位体积内能呈线性关系。压力定义为
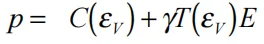（17.8.1）
增加加载（压缩）。卸载发生在峰值（最大压缩）体积应变处的体积模量对应的斜率处，如图17.1所示。重新加载沿着卸载路径一直进行到开始卸载的点，然后继续按照式（17.8.1）描述的加载路径进行。
9、状态方程形式9：Tabulated
表中的状态方程模型与内能呈线性关系。压力为
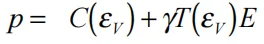（17.9.1）
体积应变εV由相对体积的自然算法给出。在定义表格函数时，最多可以使用10个点，最少可以用2个点。如有必要，可以外插出该压力。与状态方程8不同，加载和卸载是沿同一曲线。
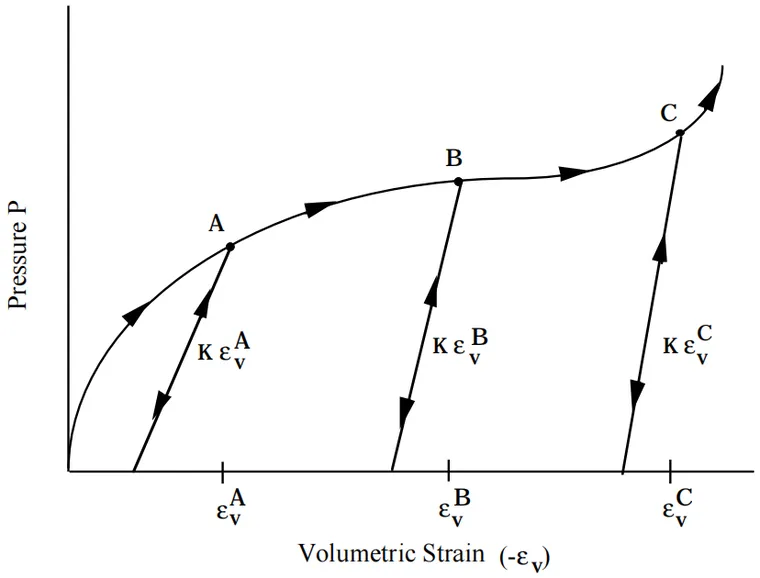
图17.1.8状态方程的压力与体积应变曲线。在压实状态下，体积卸载模量取决于峰值体积应变。
10、状态方程形式10：Propellant-Deflagration
爆燃（燃烧速率）反应性流动模型需要一个未反应的固体状态方程、一个反应产物状态方程、一个反应速率定律和两种（或更多）物质的混合规则。标准点火和生长模型的混合规则[Lee和Tarver 1980]假设，随着反应的进行，压力和温度都是完全平衡的。
然而，可以修改混合规则，不允许反应产物气体热传导或部分加热固体。对于这种相对缓慢的安全气囊推进剂燃烧过程，热平衡和压力平衡假设是有效的。目前在燃烧模型中使用的状态方程是JWL、Gruneisen、范德瓦尔斯共体积和完美气体定律，但其他的状态方程可以很容易地实现。
在这种推进剂燃烧中，燃烧的叠氮化钠产生的气体氮在充满安全气囊的气中时，遵循完美的气体定律，但可能必须被建模为在推进室内产生的高压和温度下的范德瓦尔气体。化学反应速率定律与压力、颗粒几何形状和表面积有关，以及大多数高压燃烧过程。当反应体系的温度分布已知时，可以使用与温度相关的阿伦尼乌斯化学动力学。
由于安全气囊推进剂的组成和性能数据是公司的私人信息，因此很难获得燃烧速率建模所需的信息。然而，帝国化学工业（ICI）公司提供了压力指数、粒子几何形状、堆积密度、反应热和大气压力燃烧率数据，这使我们能够开发他们的叠氮化钠+三氧化二铁驱动安全气囊推进剂的数值模型。[Hallquist等人，1990]描述了爆燃模型及其实现和ICI推进剂的结果。
未反应的推进剂和反应产物状态方程的形式均为：
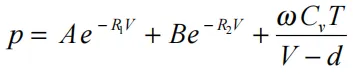
其中p为压力（以Mbars表示），V为相对比体积（相对密度倒数），ω为Gruneisen系数，Cv为热容（以Mbars-cc/cc°K表示），T为温度°K，d为共体积，A、B、R1和R2为常数。设置A=B=0。得到范德瓦尔的上体积状态方程。JWL状态方程通常在超过几千巴的压力下有用，而范德瓦尔方在压力低于该范围和高于完美气体定律成立的范围时有用。当然，设置A=B=d=0可以得到完美的气体定律。如果使用准确的ω和Cv值加上“冷”压缩和内能之间的正确分布，计算出的温度非常合理，因此可以用来检查推进剂的性能。
推进剂爆燃过程所用反应的反应速率如下：
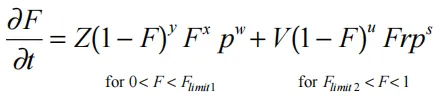
其中F是反应的分数（F = 0意味着没有反应，F = 1是完整的反应），t是时间，p是压力（以Mbars），r、s、u、w、x、y、y、极限1和极限2是用于描述反应速率的压力依赖性和表面积依赖性的常数。如果推进剂是混合物或在某种压力或温度下表现出反应速率的急剧变化，则包括两个（或更多）与压力有关的反应速率。燃烧表面积的依赖关系可以用（1-F）y Fx项来近似。
其他形式的反应速率定律，如与阿伦尼乌斯温度相关的e-E/RT型速率，也可以使用，但这些需要非常精确的温度计算。虽然LS-DYNA理论手册17.8压力的理论证明还不完整，但大量的实验燃烧速率与压力数据确实证明了这种效应，使用压力依赖燃烧的水动力计算准确地模拟了这种实验。
爆燃反应流模型被反应材料中一个或多个区域边界上的任何压力或粒子速度的增加所激活。这种增加在这些区域产生了压力，并开始分解。如果压力减轻，反应速率就会降低，并可以降为零。
这一特征对于短时间的部分分解反应很重要。如果压力保持不变，反应的分数最终达到1，材料就完全转化为产物分子。用该模型计算出的几种推进剂通过推进剂的爆燃前推进速率与实验观察到的燃烧速率与压力曲线非常接近。
为了获得与实验爆燃数据的良好一致性，该模型需要准确地描述未反应的推进剂状态方程，要么对实验压缩数据进行分析拟合，要么基于以前使用类似材料的经验进行估计拟合。对于反应产物的状态方程也是如此。现有的实验燃烧速率、压力产生和能量传递数据越多，反应速率方程的形式和常数就越好。因此，在燃烧子例程中使用的压力方程
其中，Vu和Tu分别为未反应的推进剂的相对体积和温度。相对密度显然是相对体积的倒数。反应产物中的压力Pp为：
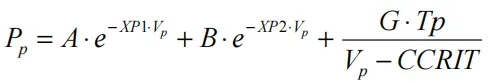
随着反应的进行，假设未反应和产物压力和温度是平衡的（Tu=Tp=T p=Pu=Pp），相对体积是相加的：
其中，V为总相对体积。其他的混合假设可以并且已经在不同版本的DYNA2D/3D中使用过。反应速率定律的形式：
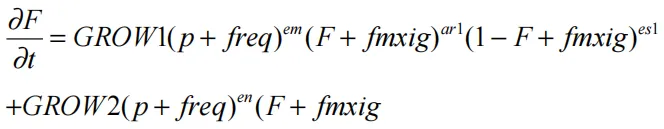
如果F超过FMXGR，则将GROW1项设为零，如果F小于FMNGR，则GROW2项为零。因此，两个独立（或重叠）的燃烧速率可以用来描述推进剂分解的速率。
这个状态方程子程序与一个材料模型一起用于描述推进剂。在安全气囊推进剂的情况下，可以使用零材料模型（type#10）。当确定剪切模量和屈服强度时，材料类型#10通常用于固体推进剂或炸药。推进剂材料由材料模型和反应开始前的无反应状态方程来定义。使用计算出的混合态，直到反应完成，然后使用反应产物的状态方程。假设反应热ENQ是一个常数，在F的所有值下都是相同的，但可以实现更复杂的能量释放定律。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
