Isight中三类优化算法比较
Isight优化算法可分为梯度算法、直接搜索法和全局优化法。梯度算法通过在设计空间中的当前位置设定一个前进方法和搜索步长从而获得设计空间中的另一个位置,并判断收敛性,Isight中梯度优化算法有三种NLPQL,LSGRG和MMFD。直接搜索法不用计算函数的梯度,仅需要函数值评估,可以有效探索初始设计点周围的局部区域,Isight中提供的直接法有HJ(Hooke-jeeves)和DS(downhill simplex)方法。全局优化法具有搜索全局最优解的,但计算耗时多,Isight中提供的全局优化算法有MIGA,ASA和PSO。本文通过一个双峰的不完全可行域问题来比较三类优化算法求解全局最优解的效率。
优化问题:
max f(x)=60/(1+(x1+1)^2+(x2-3)^2)+20/(1+(x1-1)^2+(x2-3)^2)+30/(1+x1^2+(x2+4)^2)
s.t. –((x1-2)^2+x2^2<-4.0
-5<x1<5
-5<x2<5
优化算法分别选用NLPQL,HJ和MIGA。
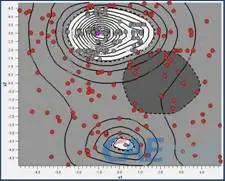
局部解(0,-4),f(x)=31.57;全局解(-0.97,3),f(x)=64.63,如图1所示。
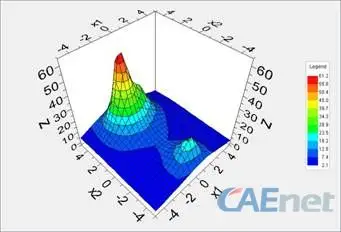
图1 目标函数的等值面
isight优化步骤:
1、构建优化流程,application组件采用calculator,process 组件选用optimization;
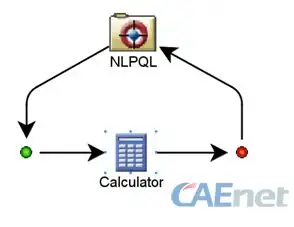
图2-优化流程构建
2、设置优化算法、设计变量、约束及目标,设计变量初始值等;
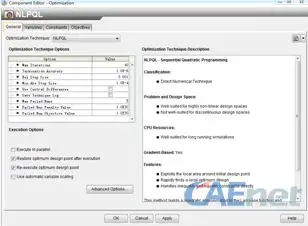
图3-优化算法及参数设置
3、查看优化结果,并比较3种算法搜寻全局最优解的效率。
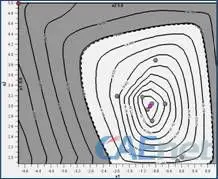

a)NLPQL,迭代28次
b)Hook-jeeves,迭代96次
c)MIGA,计算次数=1000
图4给出了三种算法的搜寻历程,初始点为(0.0,2.0),NLPQL算法迭代28次能搜寻到全局最优解(-0.972,3.000),Hook-jeeves算法迭代96次找到全局最优解(-0.972, 2.998),MIGA计算1000次找到全局最优解(-0.9693,2.7964)。图5给出了初始点(0,-2.0)两种算法的迭代历史,NLPQL迭代23次搜寻到局部最优解(0,-3.995),Hook-Jeeves迭代96次搜寻到局部最优解(0 -3.993)。以上结果可以发现,梯度算法NLPQL和直接算法Hook-Jeeves受初始点影响较大,因而有可能陷入局部最优解,但梯度算法NLPQL搜寻速度更快。而全局算法MIGA能用相对多的计算次数搜寻到一个全局最优解。
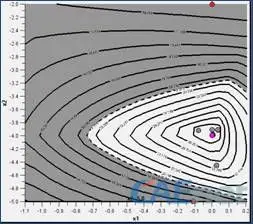

a)NLPQL,迭代23次
b)Hook-Jeeves,迭代96次
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删