注:自己做的作业,截图的时候有点混乱,有许多漏洞,望多多包涵。
一、建立物理模型
波浪理论采用微幅波,波浪的周期T=0.89s,水深h=0.4m,波高H=0.125m。二维数值波浪水槽总长13m,高1m,水槽底面的前3m是水平的,后10m是坡度为1/15的倾斜坡面。

图1 整体模型
二、网格划分
本模型采用CFD专业网格划分软件ICEM划分流体计算域的网格,网格划分选择非结构化网格。为了更好地捕捉到自由液面(及水气交界面)并得到水底流场的变化情况,在水平面处进行网格加密,且水下网格的整体尺寸小于空气网格的尺寸。网格节点加密时主要通过Exponential2和BiGeometric两种划分原则,使节点呈不均匀分布。图2是划分结构化网格时的Block分布。
图3是入口处的截图,可以明显看到网格的分布情况,其中上部分为空气,下部分为水,中间是自由液面。

图2 Block分布

图3 入口处网格分布
一共有133272个单元,图4是网格总体质量分布图,网格质量基本接近于1,说明网格总体的质量较好。图5是网格长宽比值的分布,其中单元的最大长宽比为11.4,最小长宽比2.08,长宽比越接近于1越好,最好不要超过18,所以网格质量符合计算的要求。
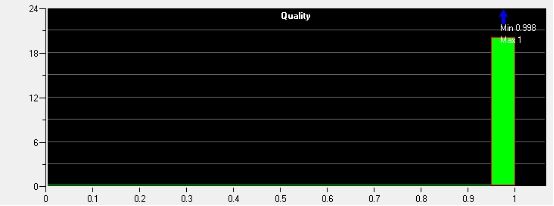
图4 网格总体质量
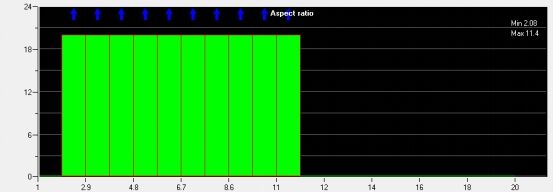
图5 网格长宽比值分布
三、Fluent计算过程设置
整个过程采用瞬态分析,由于本文中y为竖直方向,所以在y方向施加重力加速度9.81m/s^2。波浪自由液面的捕捉采用VOF方法,主要通过求解流体体积输运方程,前面已给出方程形式。总体为两相流模型,所以整个模型只有水相和气相。然后借用明渠模型进行造波,体积分数参数方程采用隐式算法,体积力方程中采用隐式体积力,设置过程如图6所示。
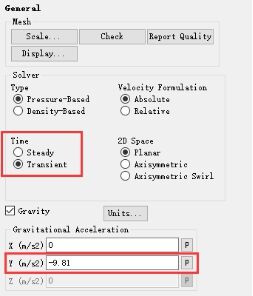
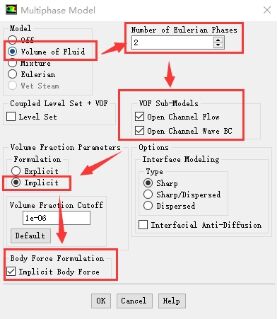
图6 通用设置和VOF设置
湍流模型选用RNG k-epsilon两方程模型。壁面函数选用Scalable Wall Function,该壁面函数对于任意细化的网格,能给出一致的解。空气的密度为1.225kg/m^3;水的密度为998.2kg/m^3,动力粘度为0.8937kg/(m·s)。
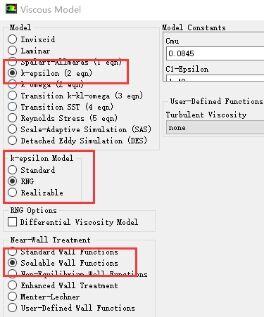
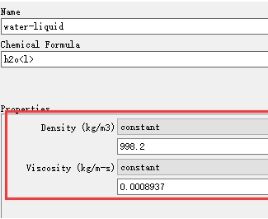
图7 湍流模型和材料参数设置
相设置中,空气为主相,水为次相。操作环境设置为标准大气压101.325kpa,参考压力的位置为自由液面处,即y=0.4m处
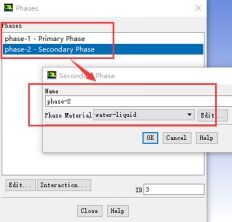
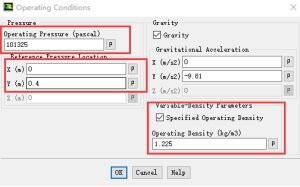
图8 相和操作环境设置
边界条件的设置如图9所示,因为模型为斜坡海岸的简化模型,所以底部设置为固壁边界条件,入口设置为速度入口,出口和顶部均设置为压力出口,计算域设置为Mixture混合流体。
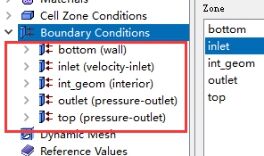
图9 边界条件设置
速度入口要选用Open Channel Wave BC,在多相设置中设置波浪边界条件为中浅水波,自由液面离底部的高度为0.4,水底为y=0m处,波浪理论选用二阶Stokes波浪理论,波高为0.125m,波长为1m,波浪的相位差和波头角均为0。压力速度耦合方法采用SIMPLE算法,压力项为PRESTO格式,对流项采用二阶迎风格式,。
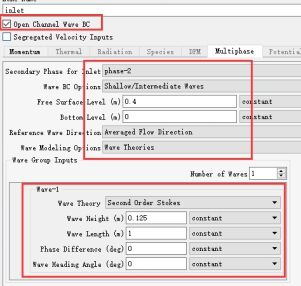
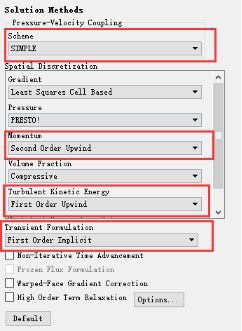
图10 造波和求解方法设置
初始化采用从入口的混合初始化,初始化方法为Flat初始化。时间步长设置为0.01s,总步长数为4000步,最大迭代次数为50。
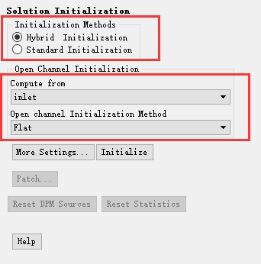
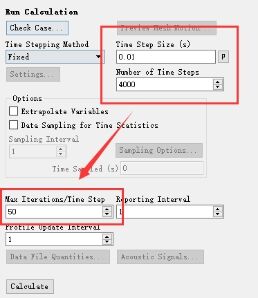
图11初始化和时间步长相关参数设置
五、计算结果分析
计算完成后,通CFD-POST软件进行后处理,分别得到速度矢量云图和压力云图。
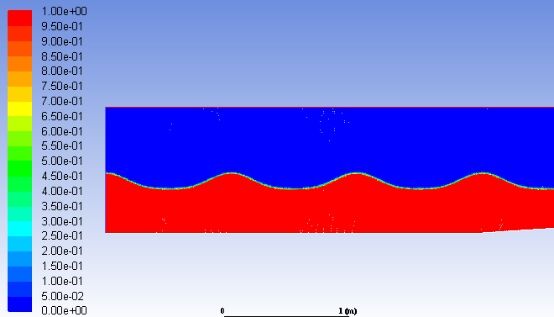
图12 二阶Stokes波浪形状

图13 稳定过后的波浪形状
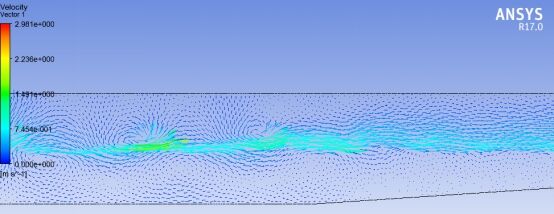
图14 速度矢量图
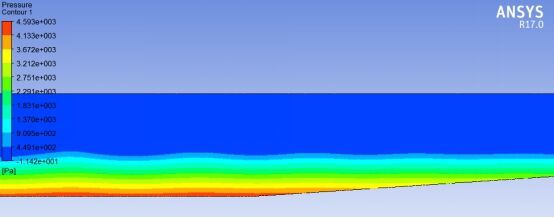
图15 压力云图
从速度矢量图中可以看出流体质点环形运动,符合基本的物理现象,压力随水深呈梯度变化,同时可以看出数值水槽可以较好地模拟波面变化。论文不足的地方是:波峰应随水深变浅而逐渐变陡,但在Fluent中由于波浪衰减较快,波浪能量耗散较大,此现象不是很明显。
图16是利用Xflow模拟出的结果,由于相关参数和边界条件设置大同小异,这里不再展示具体过程,此软件与Fluent不同的是:它采用的计算方法是格子-玻尔兹曼方法,网格采用的是笛卡尔网格。可以看出Xflow模拟的效果更好,同时可以间接说明Fluent为了得到较好的稳定性而使数值耗散比较严重。图17是卷浪的局部放大图,可以看出格子-玻尔兹曼方法在观察某一质点的细节运动时较Fluent具有明显的优势。

图16 Xflow中模拟的结果

图17 粒子追踪的卷浪效果
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删