摘 要:
目前对电厂疏水管道阀门泄漏多采用基于传热原理的内漏自动检测计算方法,但是已有研究尚未对阀门泄漏时管道内流体的流动和传热进行分析,且对温度测点如何布置以及温度测量的精度要求也缺乏研究。针对以上问题,采用计算流体力学仿真的方法,研究了阀门泄漏时管道内传热和流动情况,分析了不同的管道直径和保温材料对所测温差和泄漏量的影响。研究结果为实时监测阀门附近流量的动态变化,进行工程现场诊断疏水阀门的泄漏故障提供了模型方法和参考。
关键词:疏水;阀门;计算流体力学;Fluent软件;
热力系统阀门内漏是目前我国火力发电厂普遍存在的重大节能问题,通常由于运动部件卡死、阀片变质、弹簧应力松弛等原因造成阀门损坏[1],防止阀门内漏是火力发电厂节能减排的重要举措。阀门主要用于控制电厂锅炉和电气设备的流体介质的通路和断路调节,是电厂广泛使用的热力设备。阀门的基本功能是接通或者切断管路介质的流通,改变介质流动方向,调节介质的压力和流量,保护管路和设备正常运行[2]。
但是由于各种原因,阀门泄漏经常发生在火力发电厂当中,无论哪一个疏水阀门发生内漏,都会为电厂带来超出想象的损害[3]。目前,电力、石化、制冷等企业检测阀门内漏的方法主要依靠定期维修,对阀门进行拆卸、检修和更换。
经调查统计,超过50%的阀门并不需要进行拆卸修理,过度拆卸会浪费大量人力、物力和财力,阀门维修更换费用约占了电力企业、石油化工企业维修更换费用的15%[4]。当旁路阀门的泄漏量达到主蒸汽流量的2%时,将使供电煤耗上升4 g/(kW·h)[5]。针对现场使用的阀门监测及检修等易耗品不易购买的问题,陶长兴等[6]提出基于CRIO的嵌入式阀门诊断系统。
常毅君等[7]总结了阀门温度变化智能监测的判断依据,为电厂疏水管道的实时监测提供了新的方法。张秀华等[8]提出利用金属波纹管摇摆实验监测阀门泄漏的新方法,给出产品实验技术的研究和实施过程,为后期产品设计提供了有效的数据。
汪洋等[9]提出利用霍尔传感器监测球阀的变化状态,利用移动网络报告球阀动作时间及状态。陈启卷等[10]提出基于物联网的阀门智能系统,通过远程采集安装在水电站的阀门实时运行信息,判断阀门的运行状态,并及时监测维修。
因此,科学的管阀检修能够防止因管阀问题而产生的外泄漏事故,不仅降低了对附近设备以及工作者造成事故的几率,还防止了发电厂可能出现的不必要损失。
目前,疏水管道阀门常用的检漏方法主要有以下几种:示踪检漏、声发射检漏、红外测定法检漏、超声波检漏和压力检漏[11]。
但对于系统庞大、结构复杂的火力发电厂来说,以上各种检漏方法均存在一定的缺陷,往往达不到预期效果。同时,温度测点的布置对于泄漏量的监测起着重要作用,对疏水管道温度测点的合理布置,能有效监测泄漏量。
前人的研究多集中在对传热学的研究,而对管内流体的流场和温度场的模拟涉及的不多。对于温度测点的布置几乎没有文献涉及,合理布置温度测点,才能正确监测阀门泄漏量。
因此,本文基于已有的基于传热原理的电厂阀门内漏自动测试方法,结合电厂现场测量实例,运用传热学和流体力学的相关知识,模拟阀门泄漏时疏水管内工作流体的流场和温度场变化,从而判断温度探点的合适位置,为电厂阀门泄漏实时监测与维修提供判据,有利于在实际生产中减少阀门拆卸的次数,更加精确地判定阀门实时工作状况,从而给工作人员监测、预防电厂阀门泄漏提供合理的依据。
电厂蒸汽疏水管道-阀门监测系统主要由蒸汽管道、疏水管道、温度传感器、疏水阀门和疏水扩容器(或凝汽器)组成。系统的一端与蒸汽管道(或联箱、气缸等蒸汽容器)相连,另一端与疏水扩容器(或凝汽器)相连。电厂疏水管道-阀门监测系统示意图如图1所示[12]。其中,L1表示疏水管道竖直段长度,m; L2表示水平段到温度传感器1之间的距离,m; L3表示温度传感器1和温度传感器2之间的距离,m。
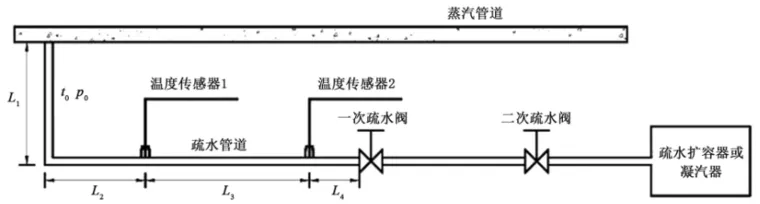
图1 电厂中疏水管道-阀门监测系统示意图[12]
当疏水管道阀门严密、未发生泄漏时,疏水阀前两温度传感器之间由于没有气体流动,只有热传导而无热对流,此时疏水管内工质流动趋于稳定,散热量为定值,管壁的温度分布趋于稳态。当疏水管道中的阀门发生泄漏时,疏水管道内部有高温工质流动。此时管内工质通过对流和热传导经过管壁和保温层向室外环境放热,随着泄漏量的增加,管道内外温差越来越小。因此,监测温度传感器1和温度传感器2的温度,通过泄漏量与温度之间的非线性关系,可以求得泄漏量的大小。
对疏水管道内流体进行建模时,考虑到主蒸汽管道入口为过热蒸汽,出口不考虑截止阀后流体流动时也可近似为过热蒸汽。由于流速较低,可视为不可压缩流体。湍流采用雷诺平均控制方程的Favre方法建模[13]。
稳态的不可压缩的单相流控制方程组包括质量、动量、能量和k-ε湍流方程:
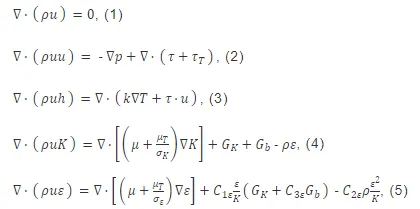
其中,ρ是流体密度,u是速度矢量,p是流体的压力,τ是应力张量,k是流体的导热系数,T是流体的温度,K是流体的湍动能,μ和μT分别是流体的动力黏度和湍流的动力黏度,σK是K的湍流普朗特数,ε是湍流耗散率,σε是ε的湍流普朗特数,GK表示由平均速度梯度产生的湍流动能,Gb是由浮力产生的湍流动能,最后,C1ε、C2ε、C1ε常数取决于使用的k-ε湍流模型。
通常,对于电厂中管路内部流体复杂的流动,通过试验进行可视化是很困难的,但疏水阀门内漏也会给企业造成巨大的损失。因此,本文利用Solidworks软件进行疏水管道的三维建模,假设阀门处有轻微泄漏,故出口假设成一根微小的管路,相较于输水管路内径可以忽略不计;用ANSYS ICEM CFD进行网格划分和流体域、固体域的创建,用商业软件Fluent进行管内流场的模拟,具体计算步骤如图2所示。
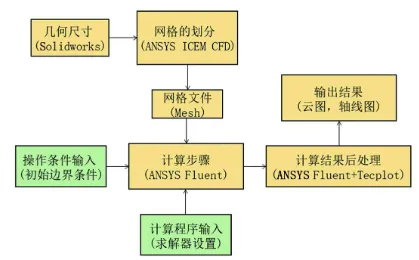
图2 阀门监测计算步骤
本文采用基于压力的求解器求解管道内流体流动,压力的求解器被用在低速不可压缩流动中。近壁面的处理和y+的设置在不同的湍流模型中有不同的差异,主要取决于使用的湍流模型,由于数学结构的特点,本文采用的k-ω湍流模型不需要近壁面处理。入口边界条件设置为速度入口,出口边界条件为压力出口。将湍流边界条件设置为水力直径和湍流强度。在压力-速度耦合项,采用SIMPLE方法对压力求解,扩散项采用二阶中心差分格式,对流项采用二阶迎风格式,当质量方程、动量方程和能量方程的残差都小于10-6时,可视为计算收敛[14]。使用理想气体模型对过热蒸汽进行处理,计算流体力学(computational fluid dynamic ,CFD)求解方法如表1所示。
表1 CFD求解方法
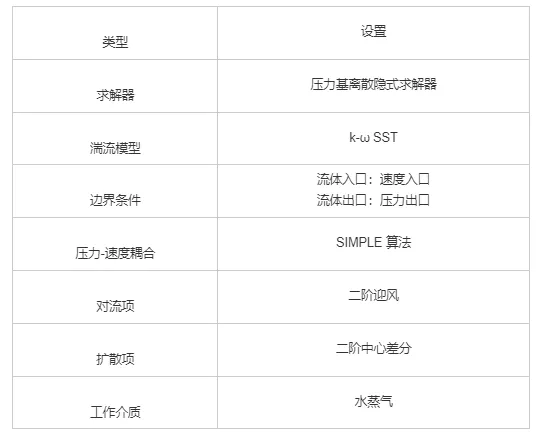
本文设计的蒸汽疏水管道-阀门监测系统根据文献[12]中的实验工况和实验数据,对比模拟和实验数据结果的误差。实验工况:进口工质压力为16.7 MPa, 温度为537 ℃,疏水管道环境温度32 ℃。实验采用了两种疏水管道,内径分别为50 mm和70 mm, 壁厚都为3.91 mm, 保温层厚度都为90 mm, 疏水管道长度均为25 m。本文验证了上述论文实验中测点(温度传感器)1和测点2的实验温度与本文程序所计算出来的管壁温度,对比结果如图3所示。从图中可以看出测点1和测点2的最大误差分别为2.46 ℃和3.13 ℃,平均相对误差分别为0.20%和0.23%,模型结果与刘功春[12]的实验结果基本吻合,表明模型准确可靠。
为了保证后续数值计算的正确性,采用文献[12]相同的边界条件,并将设计程序理论计算获得的管道出口温度与CFD模拟结果进行比较。 图4为对比结果,从图中可以看出模拟值与实验数据误差均在0.5%以内,误差在允许范围内。因此,本模型可以用于疏水管道沿管壁的温度场分布的预测。
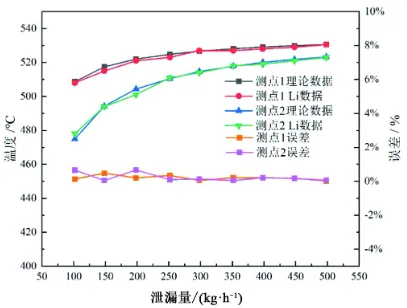
图3 模型计算与刘功春[12]实验结果对比图
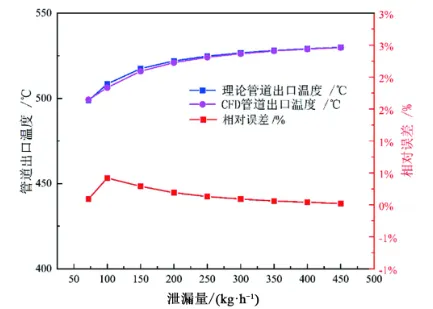
图4 理论管道出口温度与CFD模拟管道出口温度的对比
在流体力学计算中,建立优质的网格结构是计算的重要前提,决定了计算是否会收敛和结果的准确性。网格无关性验证是在保证网格质量和模拟准确性的前提下,将网格数量降低至符合运行要求的最低值。本文中的模型采用了1 347 262、2 122 552和3 525 712三种不同网格数量的喷射器二维结构,如图5所示,不同网格数的计算结果误差均符合要求,与1 347 262相比,其他两个误差为0.23 %和 0.05 %。在满足计算精度的情况下,考虑计算资源的合理利用,本文选取1 347 276网格模型作为计算网格,计算结果具有网格独立性。
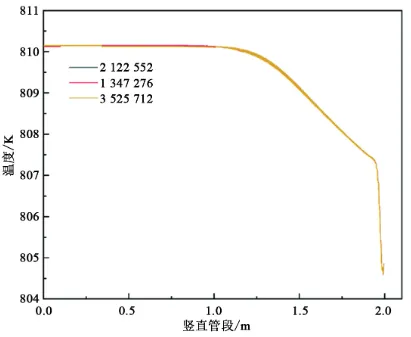
图5 竖直管段温度沿轴向变化曲线
图6为在不同泄漏量的情况下,疏水管道沿流动方向温度变化云图。从图中可以看出,随着流动距离的逐渐增大,流体温度逐渐降低,一方面是流动过程中的流动阻力和沿程阻力导致过热蒸汽在输水管道流动时有能量的损失,温度下降;另一方面为在流动过程中管内流体沿径向与管壁和保温层之间的导热,将热量散发到外界环境,导致温度逐渐降低。此外,随着泄漏量的增大,沿流动方向相同测点(测点1和测点2)的温度逐渐升高且温度沿径向分布越来越均匀,越来越趋于流体中心温度,也进一步验证了泄漏量越大,测点温度越高。

图6 不同泄漏量下疏水管道沿流动方向温度变化云图
测点布置的位置对于监测阀门外壁面温度具有重要意义,准确的测量位置能够更准确地预测阀门泄漏量。图7为疏水管道弯头前后径向温度分布云图。流体在管道内流动时,在转弯处由于局部阻力的影响,温度会发生剧烈的变化,而疏水管道上测点的布置对于合理监测管内水流量的变化具有重大意义。从图中可以看出,温度在弯管前0.50 m沿径向分布相对均匀,随着流体流动的方向,温度沿径向分布开始发生变化,表现为分布不均匀,不利于对管内流体温度的监测,随着流体的流动,在弯管后4.00 m左右,截面温度不再发生明显变化,温度沿径向分布趋于均匀。因此,在实际操作中,疏水管道阀门温度的检测位置应在距离弯管后4.00 m以上的位置布置,可以避免因为测点布置而导致测量误差的产生。
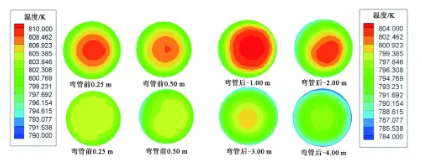
图7 疏水管道不同截面径向温度分布云图
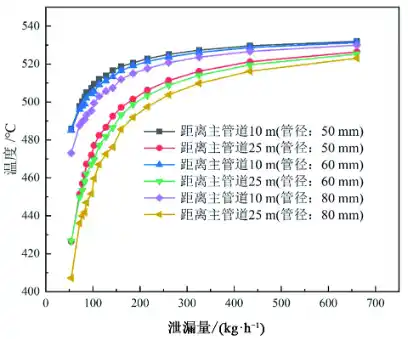
图8 不同管径下泄漏量对两测点温度的影响
通常,电厂工作人员利用测温点测得的温度与GB/T 34618—2017规范[15]中的标准进行比较,来判断是否泄漏,但是此方法不能实时给出泄漏量的大小。因此,实时计算测温点处管壁温度和泄漏量的关系对阀门内漏的在线监测具有重大意义。如图8所示,图中表示了疏水管道管径为50、60和80 mm时,不同泄漏量对两测点温度的影响,测点1距主蒸汽管道10 m(L1+L2),测点2距主蒸汽管道25 m(L1+L2+L3),测点位置如图1所示。从图8中可以看出,随着泄漏量的增加,测点1和测点2的温度均呈上升趋势,且逐渐趋于平缓。相同温度时,管径越大泄漏量越大,这是由于管径越大,管道对环境的散热量越大,相同的壁面温度下则管道内流动的泄漏工质越多。此外,相同泄漏量时,80 mm的疏水管道在测点1和测点2的温度总是低于50 mm的疏水管道。这是因为泄漏量相同时,管径越小,横截面积就越小,疏水管内工质流速越大,对流换热系数越大,流体从主蒸汽管道流到测点1和测点2的所需时间就越少,管道的热量损失少,所以温度会升高。
图9为疏水管道径向温度的分布,由于钢管的厚度为0.003 91 m, 相比于保温层的厚度0.09 mm小得多,故忽略钢管的厚度。图中可以看出A为距离主蒸汽管道1.0 m处的温度分布,B为距主蒸汽管道1.5 m处的温度分布,A处温度分布均匀,沿径向温度逐渐降低,B处温度较A处分布不均匀,尤其是保温层区域内温度有明显的波动。这是因为过热蒸汽从主蒸汽管道进入疏水管道,随着流动距离的变化,流动损失逐渐增大,在遇到转弯处流体会发生剧烈的变化,导致温度场分布不均匀,而B处距离转弯处较A处更近,故温度分布不均匀。
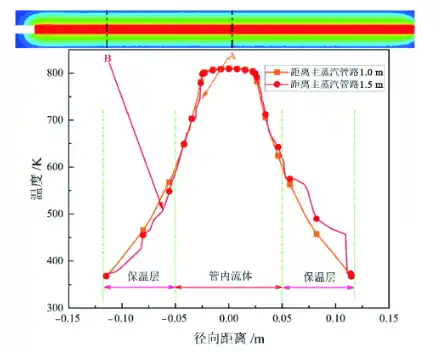
图9 疏水管道径向温度分布
图10表示在不同泄漏量下疏水管道内速度沿轴向中心线的分布。从图中可以看出,随着泄漏量的增大,管内流体流速整体呈上升趋势,转弯处,速度变化剧烈,这是由于在转弯处,流体受到来自管壁的阻力被迫改变方向,此时纵向速度急剧变化,横向速度慢慢上升,从而呈现出整体速度产生剧烈变化。此时管内流体会产生局部阻力从而导致局部损失,随着管段的增长,速度又逐渐变大。因此,在布置压力传感器时,为保证测量准确应尽可能地布置在远离速度变化剧烈处。
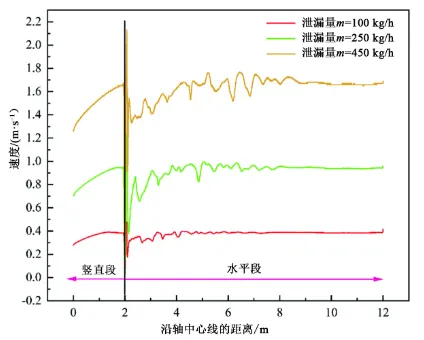
图10 不同泄漏量下沿轴向中心线速度分布
本文以电厂阀门泄漏实时监测的需求现状为切入点,建立数学模型和物理模型,运用计算流体力学软件Fluent分析疏水管道内部流场和温度场的变化,所得结果更直观地反映了疏水管道内部的温度变化,便于对电厂疏水阀泄漏实时监测。得出结论如下:
1)疏水管道内部流体温度沿流动方向逐渐降低,且随着管道内径的增加而逐渐增大。
2)由于沿程阻力和局部阻力的影响,流体在流动过程中会在转弯处产生温度沿径向分布不均匀的现象,在弯管前0.5 m、弯管后4.0 m处布置温度测点可以更好地测量管壁温度。
3)疏水管道温度沿径向逐渐降低,且距离转弯处越远,径向温度分布越均匀。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删