数值仿真探讨：圆孔应力集中现象分析

1. 应力集中是工程师经常听到并提及的概念。是重要的。
2. 本文只简单讨论静荷载下的应力集中问题。抛砖引玉。
3. 模型为开圆孔板，尺寸200mm*100mm*2mm，圆孔直径10mm。
4. 边界条件，左右边线各施加10kN拉力，方向相反。平衡。
5. 根据材料力学，产生的平均应力大约为50MPa。
6. 刘鸿文版材料力学第2章12节，标题为应力集中的概念，实在，真的停留在概念层面。对应力集中的理论分析，还需参考徐芝纶版弹性力学。

当element size为4mm时，网格和等效应力：

当element size为2mm时，网格和等效应力：

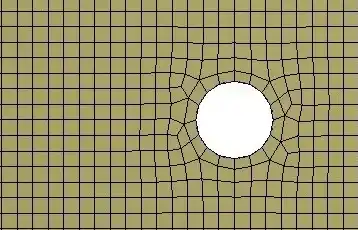
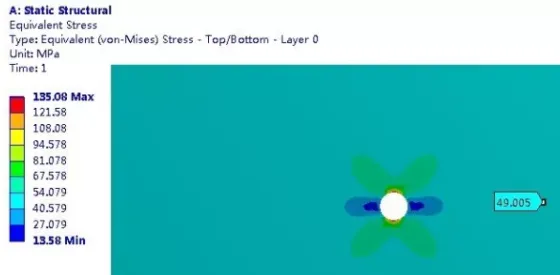
当element size为1mm时，网格和等效应力:

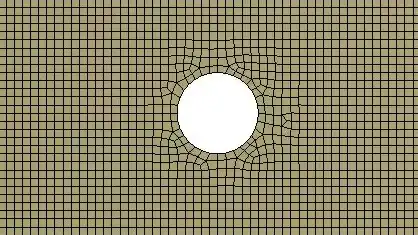
element size为0.5mm时，网格和等效应力：

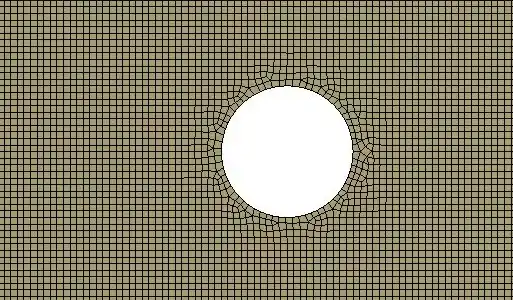
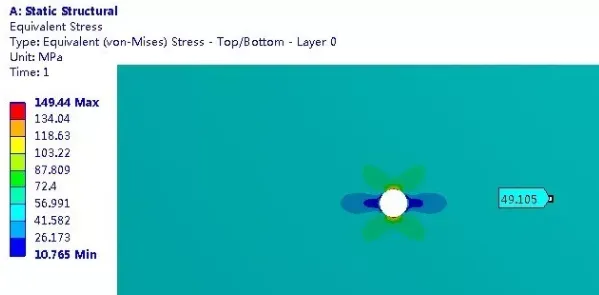
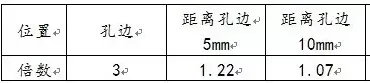
综合以上可得：除了圆孔边缘以外，其它位置的应力都接近50MPa。随着网格变细，圆孔边缘的应力在不断增加。应力集中现象明显。

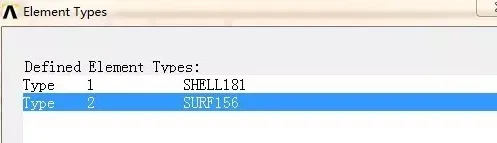
将workbench的有限元模型导入ansys经典界面，查看单元类型。shell181为4节点壳单元，为workbench计算平面问题的默认单元。surf156单元为线荷载等效单元，本例施加了线力，所以自动出现。

数值仿真中插入收敛性分析：

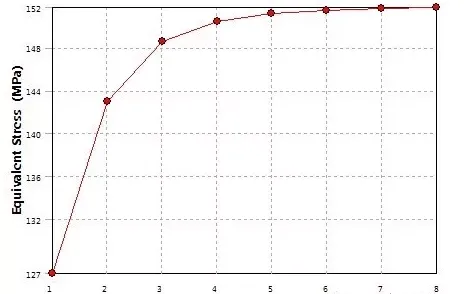
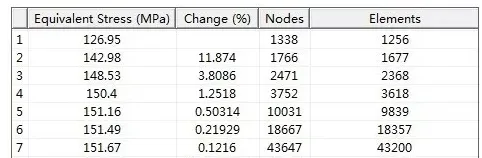
查阅相关经典理论：

对于工程师来说，弹性力学属于古典理论，意味着不掌握也没有关系，查阅徐芝纶版弹性力学。

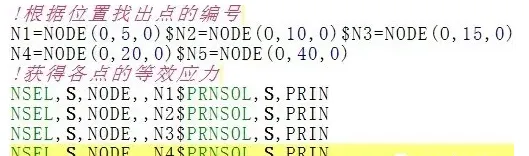
将workbench的计算结果导入到ansys经典界面，查看节点等效应力：

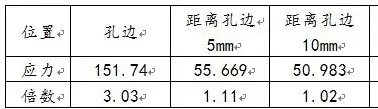
可以看出，理论和仿真基本一致，相互验证。

附：

工程中更常见的，并不是板的两边都受拉，而是一边受拉，一边固定。固定约束是很常见的约束形式，研究此情形下开圆孔板模型的收敛性问题，惊奇发现第5步之后，斜率变大了，难道是计算不收敛！非也，其实圆孔附近应力的收敛结论是不会被打破的，造成这种转折的原因是最大应力已经移位固定边界的角点上。

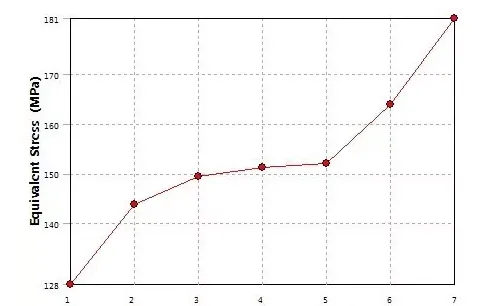
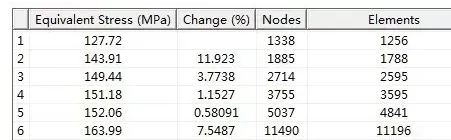
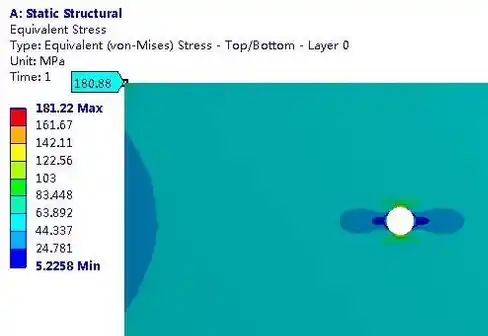
这确是个问题，随着网格变细，左边线的固定约束带来了异常。将材料的泊松比缩小100倍，再查看固定约束开圆孔板的收敛性。

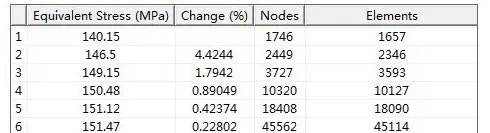
改变泊松比，收敛反转现象不再出现。

不论材料力学，还是弹性力学都建议避免构件的截面尺寸发生突变，尽量采用圆弧过渡，尽量只开圆孔或椭圆孔。开椭圆孔板的应力集中，弹性力学有分析结果，再用有限元法查看一下。

平均应力50MPa，椭圆孔水平放置时，理论上放大2倍，最大为100MPa：

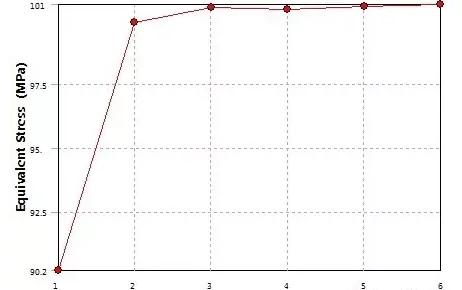
当椭圆孔垂直放置时，理论上放大5倍，最大为250MPa。如果椭圆孔再细长一点，应力计算会越来越难收敛，读者可自行尝试：

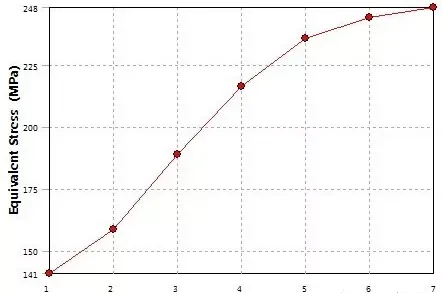
应力集中是客观存在的现象，不以人的美好愿望而转移，但可以去了解它。应力集中问题的有限元仿真需要网格细化，而网格细化的结果当然能准确表征出应力集中现象。如果构件某处存在应力集中，但分析者由于各种原因并不需要关心此处，此时的网格细化则又是画蛇添足，万万不要的。可以搬出圣维南原理来解释，不管应力集中处的网格多么差劲，距离较远处的仿真结果并不会受较大的影响。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删