1.1 田口正交法
田口品质设计法,是利用田口玄一博士[1]所设计的正交表,设计少量的参数组合,进行实验,并使用S/N比表示产品品质的好坏,以求的最佳组合,而达到高良率,低成本的重要方法。
正交表[1]为一组矩阵式数字,每一行代表一个特定实验中因素的状态,每一列代表一个特定的因素或条件组合。主要以较少的实验次数来获得有用的统计资料,正交表以La(bc)命名,代表共有a组实验,最多容纳b个水平的因子c个,以L18(21×37)为例,由1个2水平的因子和7个3水平的因子所组成,需实验18次,因此,正交表的目的在于:(1)了解控制因子(Control Factor)及干扰因子(Noise)对产品品质的影响;(2)由计算S/N比及进行变异分析(Analysis of Variance),以找出影响较大的因子,并求出最佳的参数组合。
1.2 信号噪音比(Signal to Noise Ratio)
信号噪音比(S/N)[1]是田口品质工程上重要的评估指标,可用来表示制程或产品的水平受误差因素影响的程度。有田口博士将平均品质损失经由对数转换、乘以10、并取负号,称为S/N比,由于品质特性的目标不同,故计算S/N比由品质特性可分为三种特性:
1)望小特性
S/N比越大,表示平均值越靠近0,且变异越小。即提高S/N比即可使变异变小,且平均值越靠近目标值0。
2)望大特性
3)望目特性
1.3 变异分析(ANOVA)
变异分析(Analysis of Variance)主要是评估实验误差,找出影响较大的控制因子,并利用统计分析,可辅助图表的不足。
2.1 实例背景
例如,我们在分析封装的热应力时,由于封装结构尺寸较多、材料通常比较复杂,难以每个结构以及材料都进行单因素分析,另一方面,单因素分析难以考虑到结构间、结构-材料、材料间的交互影响,因此,我们推荐利用田口正交分析,利用一定量、可控的实验分析,对结构、材料复杂,每种因素包含水平较多的实验,进行分析。
本例结构因素以及水平如下:
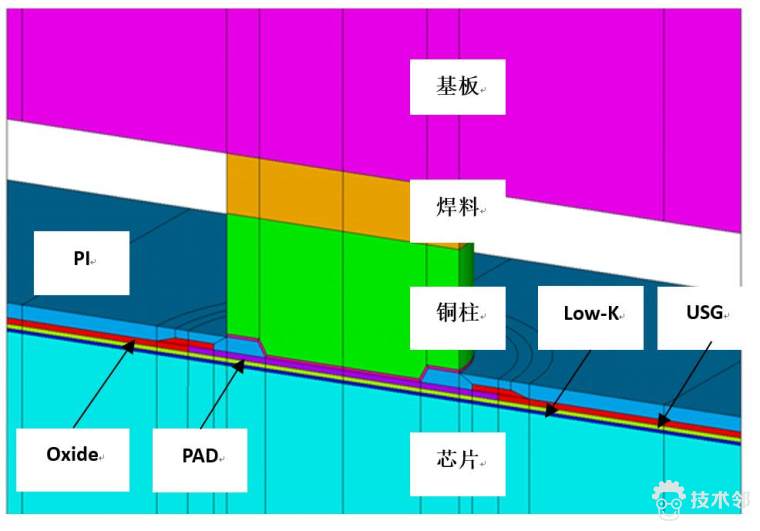
| 因子 | 单位 | 水平1 | 水平2 | 水平3 | |
| A | 芯片尺寸 | mm | 2.0 | 3.0 | 4.0 |
| B | 芯片厚度 | mm | 0.1 | 0.2 | 0.3 |
| C | 铜柱直径 | mm | 0.08 | 0.10 | 0.12 |
| D | 铜柱高度 | mm | 0.03 | 0.05 | 0.07 |
| E | 焊料高度 | mm | 0.01 | 0.03 | 0.05 |
| F | PI开口大小 | mm | 0.03 | 0.05 | 0.07 |
2.2 确定实验量
如上节,如果我们将每个因素的每个水平都进行分析,我们则需要进行3e6=639组实验,这是我们所不能接受的。
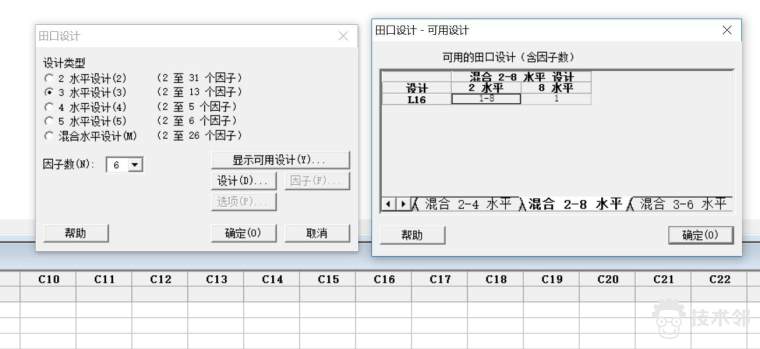
正交表的形式和计算方法在此不做详细讨论,实际使用中,我们可以通过软件直接选择生成正交表。
如下表为minitab软件,可以在软件中选择因素和水平后,直接生成正交表。
2.3 提取ANSYS中的仿真结果
可以在ANSYS中计算得到我们关注结构的应力或位移等数值,如本例中的Bump中线路层中的第一主应力值,并记录在下表中,并由第一章节中的公式计算得到信噪比(dB)。
| 序号 | A | B | C | D | E | F | 第一主应力(MPa) | 信噪比(dB) |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 134.5 | -42.57 |
| 2 | 1 | 1 | 1 | 1 | 2 | 2 | 159.3 | -44.04 |
| 3 | 1 | 1 | 1 | 1 | 3 | 3 | 182.8 | -45.24 |
| 4 | 1 | 2 | 2 | 2 | 1 | 1 | 174.3 | -44.83 |
| 5 | 1 | 2 | 2 | 2 | 2 | 2 | 190.6 | -45.60 |
| 6 | 1 | 2 | 2 | 2 | 3 | 3 | 210.7 | -46.47 |
| 7 | 1 | 3 | 3 | 3 | 1 | 1 | 196.3 | -45.86 |
| 8 | 1 | 3 | 3 | 3 | 2 | 2 | 224.2 | -47.01 |
| 9 | 1 | 3 | 3 | 3 | 3 | 3 | 220.2 | -46.86 |
| 10 | 2 | 1 | 2 | 3 | 1 | 2 | 102.3 | -40.20 |
| 11 | 2 | 1 | 2 | 3 | 2 | 3 | 121.7 | -41.71 |
| 12 | 2 | 1 | 2 | 3 | 3 | 1 | 96.8 | -39.72 |
| 13 | 2 | 2 | 3 | 1 | 1 | 2 | 177.0 | -44.96 |
| 14 | 2 | 2 | 3 | 1 | 2 | 3 | 198.3 | -45.95 |
| 15 | 2 | 2 | 3 | 1 | 3 | 1 | 221.1 | -46.89 |
| 16 | 2 | 3 | 1 | 2 | 1 | 2 | 333.3 | -50.46 |
| 17 | 2 | 3 | 1 | 2 | 2 | 3 | 349.9 | -50.88 |
| 18 | 2 | 3 | 1 | 2 | 3 | 1 | 289 | -49.22 |
| 19 | 3 | 1 | 3 | 2 | 1 | 3 | 76.3 | -37.65 |
| 20 | 3 | 1 | 3 | 2 | 2 | 1 | 67 | -36.52 |
| 21 | 3 | 1 | 3 | 2 | 3 | 2 | 71.4 | -37.07 |
| 22 | 3 | 2 | 1 | 3 | 1 | 3 | 349.3 | -50.86 |
| 23 | 3 | 2 | 1 | 3 | 2 | 1 | 304.6 | -49.67 |
| 24 | 3 | 2 | 1 | 3 | 3 | 2 | 370.1 | -51.37 |
| 25 | 3 | 3 | 2 | 1 | 1 | 3 | 303.0 | -49.63 |
| 26 | 3 | 3 | 2 | 1 | 2 | 1 | 307.6 | -49.76 |
| 27 | 3 | 3 | 2 | 1 | 3 | 2 | 310.3 | -49.84 |
2.4 利用Minitab生成结果
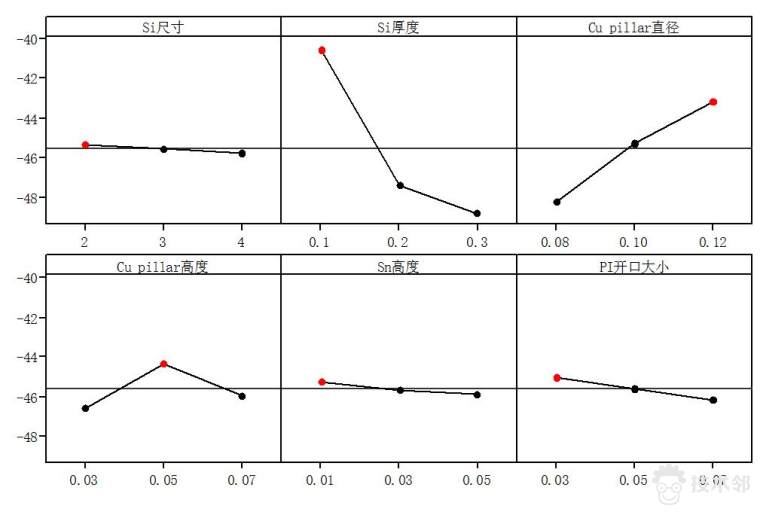
将上一节ANSYS得到的结果输入至Minitab的结果栏,注意与实验次序相一致,并于软件内进行分析,可得到如下图表所示的结果。
F、P值代表因素影响结果的强弱,一般P≤0.05即认为是影响较大的因素。
下图中红色点的含义为,当此因素的水平为红点处的数值时,此时结构因素的组合为最优组合设计。
| 来源 | 自由度 | Seq SS | Adj SS | Adj MS | F | P |
| 芯片尺寸 | 2 | 0.855 | 0.855 | 0.428 | 1.05 | 0.375 |
| 芯片厚度 | 2 | 355.094 | 355.094 | 177.547 | 436.95 | 0 |
| 铜柱直径 | 2 | 116.313 | 116.313 | 58.156 | 143.13 | 0 |
| 铜柱高度 | 2 | 24.097 | 24.097 | 12.048 | 29.65 | 0 |
| 焊料高度 | 2 | 1.903 | 1.903 | 0.952 | 2.34 | 0.133 |
| PI开口大小 | 2 | 5.794 | 5.794 | 2.897 | 7.13 | 0.007 |
| 残差误差 | 14 | 5.689 | 5.689 | 0.406 | - | - |
| 合计 | 26 | 509.746 | - | - | - | - |
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删