断裂是混凝土材料破坏的主要模式。可靠、高效的混凝土断裂模型在桥梁、隧道、大坝等土木工程结构的安全评估中发挥着重要作用。对混凝土断裂的研究,尤其对其裂纹萌生和扩展的研究,引起了国内外学者越来越多的关注。混凝土断裂的数值模拟与断裂理论、物理试验相互印证与补充,并随着科技发展不断地提高着混凝土断裂问题模拟的准确性。近年发展起来的断裂相场法,通过场变量的自动演化获取裂纹路径,可方便地模拟出裂纹的动态扩展过程。因此本案列将采用基于ABAQUS的断裂相场模型实现对混凝土断裂问题的模拟分析并探讨该模型的工程实际适用性
相场法是一种以经典热、动力学理论为基础,由耦合的非线性的力平衡方程和相场梯度型演化方程组合而成的唯象方法。该方法引入一组场变量来描述结构的相变过程。与锐界面法中场变量的不连续性相反的是,相场法中场变量在界面区域具有连续性,可以用来描述材料初始时和完全破坏之间的平滑过渡。相场变量能分成保守的场变量与非保守的场变量两种,总量在物体结构演化中保持不变的为保守的场变量,如原子和电荷的浓度场;总量在物体结构演化中为不守恒的并从0到1变化的是非保守的场变量,如马氏相变。
Frankfort和Marigo基于能量最小化原理提出了Griffith理论的变分形式。描述断裂的相场法中材料势能分为两部分,弹性应变能和表面能,分别对应于完好相和断裂相。Griffith理论的泛函形式可以表达为:
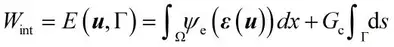
其中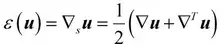 是对称的小应变张量,代表裂纹面,Ω为求解区域。断裂问题系统自由能由弹性应变能(等号右边第一项)和断裂表面能(等号右边第二项)构成,裂纹的扩展受自由能最小化原理控制。通过求能量泛函的极值可以获得材料系统的控制方程。
是对称的小应变张量,代表裂纹面,Ω为求解区域。断裂问题系统自由能由弹性应变能(等号右边第一项)和断裂表面能(等号右边第二项)构成,裂纹的扩展受自由能最小化原理控制。通过求能量泛函的极值可以获得材料系统的控制方程。
采用有限宽度的弥散区域来近似表征离散裂纹面,如图 1所示。所有场变量均是全域连续。采用一个标量d来表征材料的状态,称之为相场。d=1代表材料完全失效,d=0代表材料完好无损。通过引入序参量d,给出了断裂面的弥散表达式:
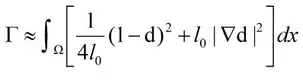
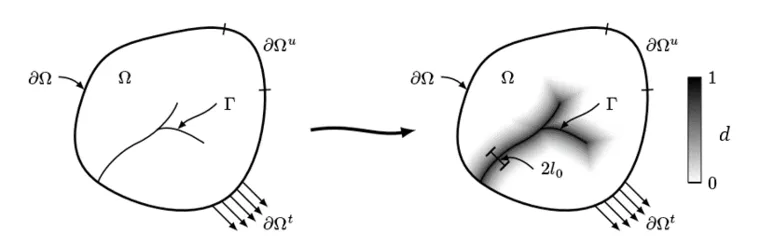
图 1 .相场法示意图
式中l为影响断裂面的弥散宽度(的区域)的长度尺度参数:l越大,裂纹弥散宽度越宽;l越小,裂纹弥散宽度越窄;当时,裂纹弥散宽度l趋于0时。代入(1)式,可得自由能:
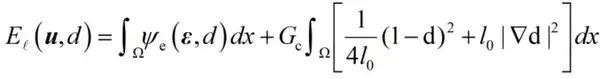 在考虑外力做功的情况下,总的自由能可以分为两部分:
在考虑外力做功的情况下,总的自由能可以分为两部分:
其中,外力功可以表达为,
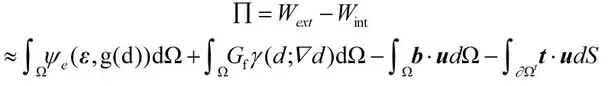
其中,b和t分别为系统体力和作用在系统表面上的面力。对式上求变分,可以获得:
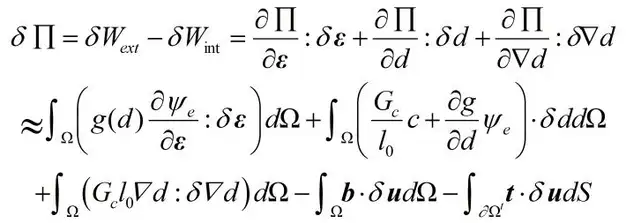
需对任意的变分场δd,δε,δ▽d都满足,意味着需要满足以下等式:
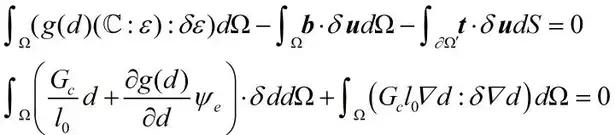
基于相场控制方程,推导其相应的有限元离散格式。形成了用于解耦相场和位移场的方程组,该方程组可用于更新相场和位移场。本研究采用交错算法对相场模型进行求解,其中交错算法示意如图 2所示。
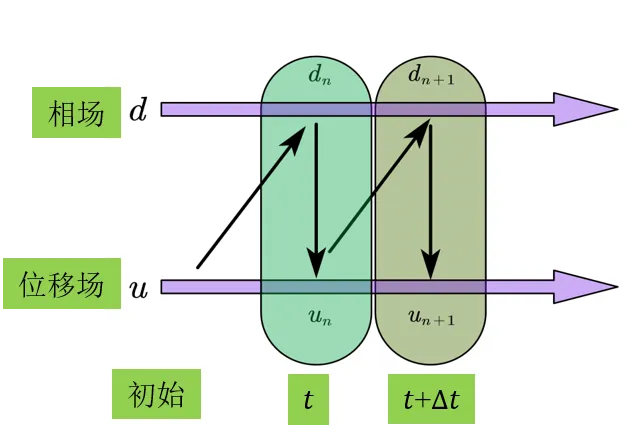
图 2 交错解法流程示意图
以上为控制方程的弱形式,通过运用高斯定理,可以得到其强形式为:
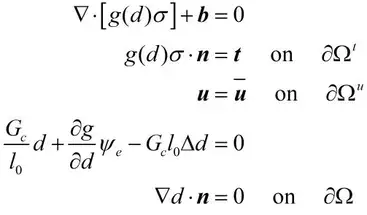
其中,▽运算符是拉普拉斯算子。为了保证相场法中裂纹的不可逆性,由于无直接的裂纹量度,因此通常从损伤力学的角度保证,即来保证裂纹的不可逆性。提使用历史变量H来代替方程中的,即
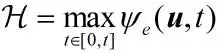
本节使用ABAQUS软件编写Fortran子程序实现基于相场法的裂纹扩展模型。对经典的混凝土试件单轴受压模拟进行相场模拟,模型如图 3所示,几何尺寸100x 100mm。采用位移控制加载方案,平板底端固定,上端压缩。其中,骨料强度大,混凝土破坏时一般骨料不会发生损伤,所以本文将骨料单元损伤本构模型的断裂能设定较大。砂浆和ITZ采用正常的相场损伤本构模型,表1.1给出了各相的材料参数,值得注意的是,损伤本构模型只需要设定杨氏模量、泊松比、抗拉强度和断裂能等常见的材料参数即可。

图 3 单边缺陷试样单轴拉伸加载示意图
表 1 各组分材料属性
| 弹模(GPa) | 泊松比 | 强度(MPa) | 断裂能(N/m) | |
| 骨料 | 50 | 0.2 | 35 | 3000 |
| 砂浆 | 20 | 0.2 | 4.5 | 150 |
| 界面过渡区 | 15 | 0.2 | 3.5 | 90 |
图 4表示为不同加载时刻下模型损伤云图,由图可以看出在初始时刻时,由于外部载荷的较小,模型损伤程度比较小,并且损伤较为分散,对应图5最终的损伤网格模型可以看出,此时损伤云图里呈现蓝色的低损伤区域对应于图5的骨料,这也和之前对材料属性的设置相一致。骨料相较于其他两项组分,由于其断裂能较大,所以不易出现损伤。随着载荷的增大,在中部区域出现聚集性损伤,且损伤程度较大,裂纹处于损伤形核阶段。随着载荷继续增大,损伤朝向左右骨料的间隙方向延伸。此时损伤继续加大,这也就意味着在能量持续输入的情况下,能量转化成裂纹表面能的比例增大。随着载荷的增大,裂纹已经完全扩展至左右两侧边界。虽然弥散裂纹不具有尖锐裂纹那种可视化拉断效果,但是从物理意义上来说,此时模型已经被完全拉断。这一点从图6模型整体的力-位移曲线也可以看出。
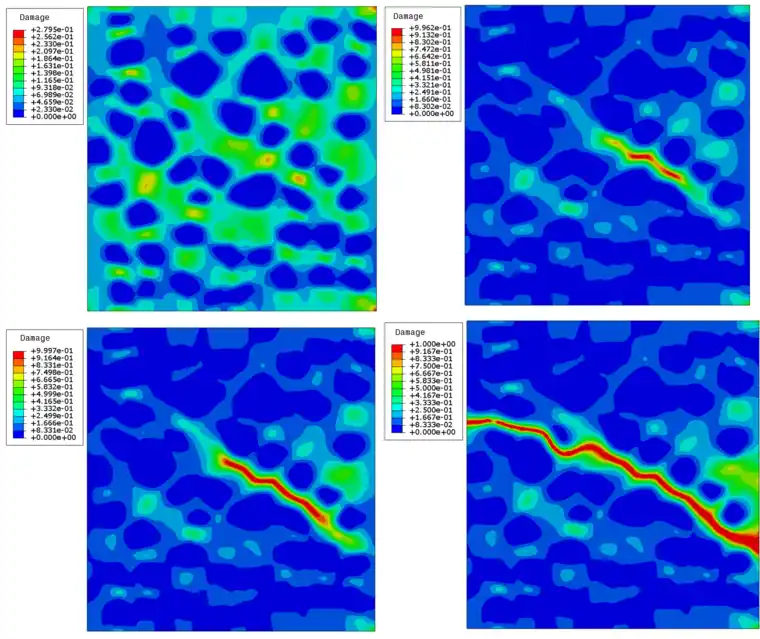
图 4 不同时刻下模型损伤云图

图 5 损伤网格模型
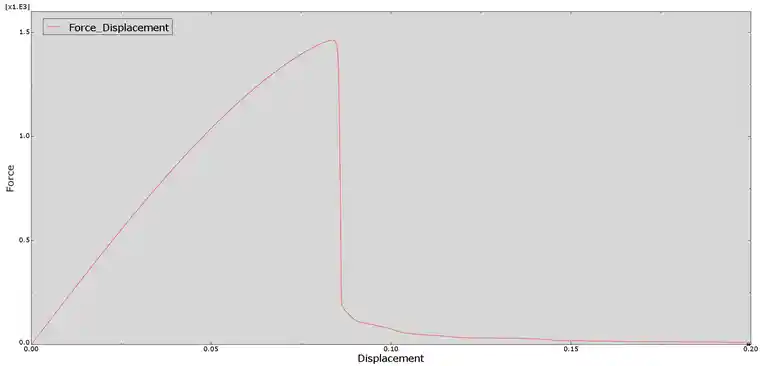
图 6 损伤本构下的力-位移曲线
1)对于界面过渡区的处理,本案例简单的采用了直接赋予材料属性的办法。该方法的科学性还需要进一步验证,之后需要进行全面的理论与数值模拟研究。
2)在工程实际当中,诸如温度、湿度等多场耦合问题也是十分常见的,对混凝土全生命周期性能影响不容忽视。研究多场耦合问题的难点在于除了需要考虑其他场与位移场的耦合关系外,对于它们与相场的耦合关系亦不容忽视,此外各自的耦合方式仍需探讨,这将会是一项有意义且有趣的研究。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删