非傅里叶热传导分析：基于Abaqus的UMATHT子程序应用

传统的热传导分析建立在傅立叶定律基础上，认为热流温度梯度为线性分布，而且热流传播速度是无限大的。随着瞬态加热技术的应用，发现即使在常温或者高温下，导热规律也可能偏离傅里叶定律。非傅里叶导热模型较传统的抛物型方程(傅里叶模型)更复杂，其热传导特性受到松弛时间的影响。非傅里叶模型具有多种不同形式，目前最常见、最普遍的模型是双曲型热传导模型。

Maxwell首先提出了双曲型热传导模型

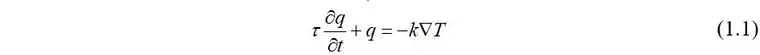
能量守恒方程为

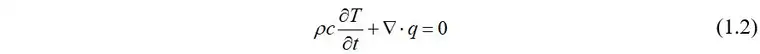
联立式1.1和1.2可得非傅里叶传热方程为

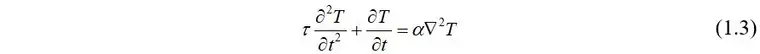
式中，T为温度，t为时间，α为介质的热扩散率，τ为热松弛时间。

Abaqus中可以通过UMATHT子程序实现式1.3的热传导模型。

建立如下图所示的有限元模型，模型上下侧为温度边界。

取τ=0，0.1，0.5，1.5进行计算，平板中心点温度变化曲线如下图所示。可以发现，随着热松弛时间变大，温度波动越明显，达到平衡所需的时间越长。

热松弛时间τ=0时，式1.1退化为傅里叶传热。

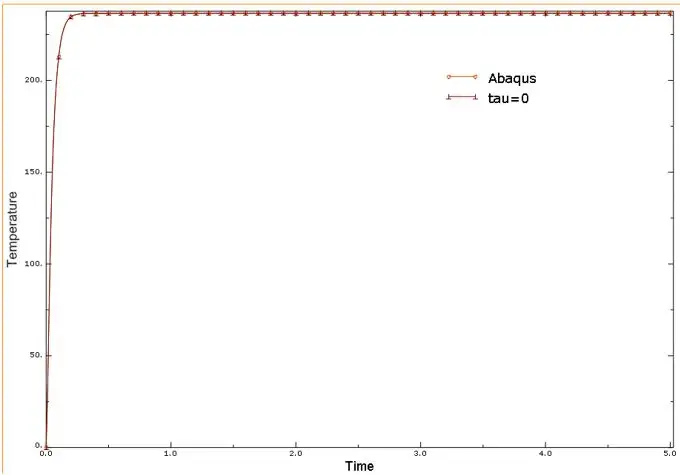
可以发现，τ=0时子程序和Abaqus自带材料属性计算得到的温度变化规律一致。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删