FLUENT直管湍流入口段模拟与计算

1 前言

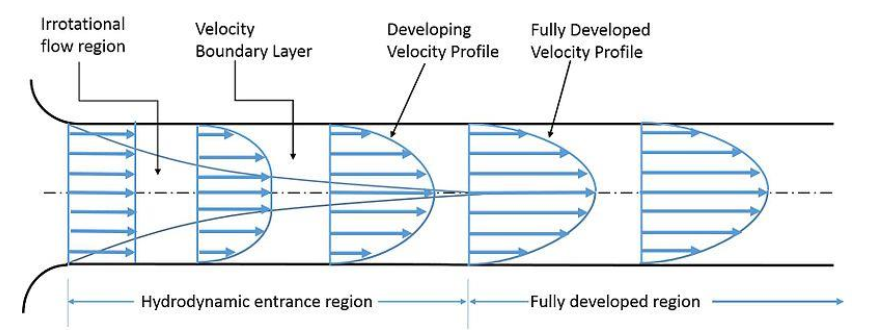
典型的直管内流动速度变化如下图，从入口到充分发展开始之间的管段称为水力入口段。在开展很多管内流动计算时常常要想办法排除入口段长度的影响，此时通常会在上游增加一定长度，以直管为例，如果要完全排除入口段的影响，整个计算域的长度必须大于入口段长度。有不少经验公式可以作为建模参考，比如湍流直管的入口段长度经常用L=4.4Re^1/6D来计算，其中Re为雷诺数，D为水力直径。今天，我们做一个直管湍流的入口段长度计算案例。

2 建模与网格

建立一根长度2m，内径8mm的光管，内部介质为水，密度998.2kg/m3，动力粘度0.001003Pa·s。分别计算在不同雷诺数下入口段长度，并与上述理论公式对比。本案例采用二维轴对称模型来计算。

3求解设置

入口采用速度入口边界，出口采用压力出口。

本案例采用了常用的几种湍流模型和近壁处理方式，对比其计算结果。包括标准k-e湍流模型，近壁处理分别为标准壁面函数和加强型壁面函数，以及SST k-ω湍流模型。

4计算结果

充分发展段的特点包括轴向速度不再变化或速度梯度为0，管道各截面的速度分布一致等等，从该位置往上游都是入口段。采用FLUENT求解入口段长度时可先获取中心轴向速度随管道长度的变化曲线，再根据上述特征来判断入口段长度，或者用轴向速度达到最终轴向速度的99.9%位置作为入口段终点来计算入口段长度，后者是FLUENT官方案例推荐的方法。

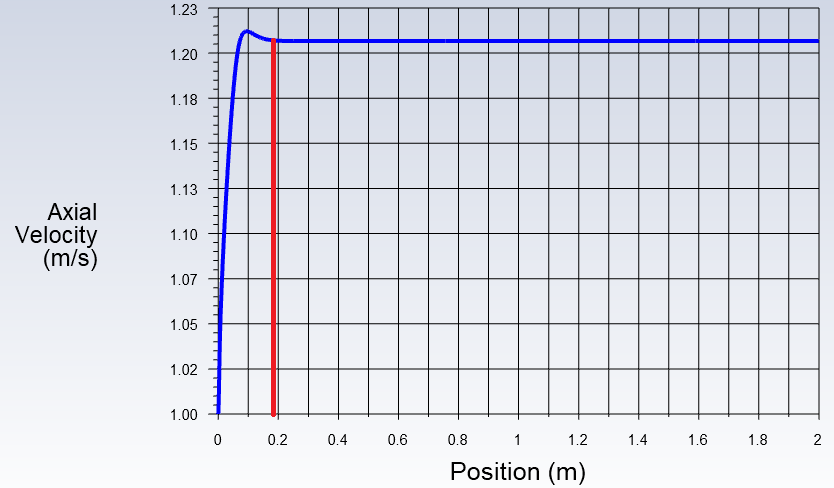
我们先取某个雷诺数下的管道中心轴向速度曲线如下，红线之前的长度即为入口段长度。另外，红线之前的速度有个凸点很诡异，这和理论分析是相违背的。笔者暂未找到原因，不知道读者朋友中有没有类似的经验可以分享一下吧。

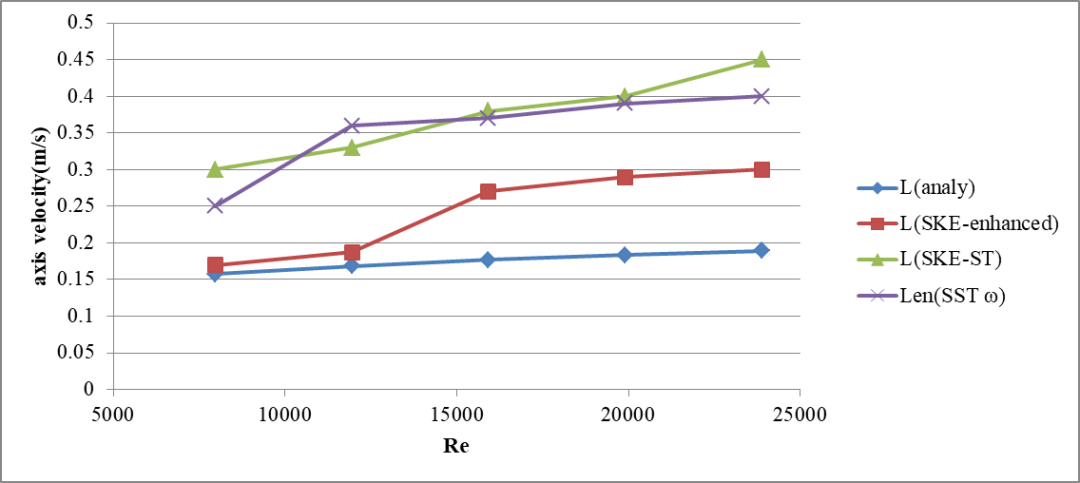
不同雷诺数下，上述几种湍流模型的入口段长度计算结果和理论公式结果对比如下，可以看出标准k-e模型+加强型壁面函数的计算结果和理论公式结果更为相符，这也是FLUENT官方案例采用的湍流模型。需要注意的是，并不是说标准k-e模型+加强型壁面函数是最好的组合，这个只是对于入口段长度计算较为贴近理论公式，对于不同问题不同的湍流模型适应性是不一样的，湍流本身就是最麻烦的，没有一个普适的湍流模型，这才是最蛋疼的。