1. 标量输运方程简介
标量输运方程是描述在空间中某个标量随时间和空间位置的变化的方程,通常用偏微分方程的形式表示。最常见的就是浓度、温度的扩散问题等
比如我们经常见到的对流换热问题,就可以表示成标量输运方程的形式

上述方程从左到右分布为瞬态项、对流项、扩散项和源项。当热扩散系数D为常数时,可以把D拿到偏微分符号外面。
标量输运方程有一个最大的特点:其方程形式基本相同,都包含上述四项。比如Fick's第二定律描述质量扩散问题,其形式为

从上图中的公式6可以看出其形式与对流换热形式基本相同,对其进行整理一下看的更明白一些,少了对流项和源项。
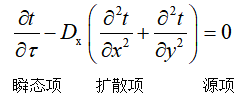
既然对于不同的标量问题,其基本方程形式都相同,这就给了Fluent可乘之机。什么可乘之机呢??方程形式相同,那只需要一个方程就可以解决所有问题了,把要求解的标量换一下就行。
这就是Fluent UDS(User-Defined Scalar)的基本原理,UDS---用户自定义标量。
注:
a. 对于UDS来说,由于方程形式相同,不在乎求解的是温度还是浓度,其本质是相同的。
b. 方程可能会少某些项,比如扩散项、对流项等,也可能会多出来一些项,比如内热源等,如何处理??
少项很简单,将这些项=0就可多出来的项,都移到方程右边作为源项,无论如何要保证瞬态项、对流项、扩散项形式要相同。
2. UDS输运方程
上面我们介绍了标量输运方程,Fluent提供了标准的标量输运方程
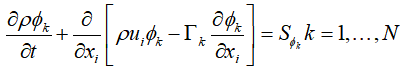
和我们给出的标量输运方程形式似乎不太一样??但实际上是相同的。这里有一点偏微分方程写法上的技巧需要说明。
3. 偏微分方程的写法
3.1 重复下标表示求和
这来源于张量的一种简化写法,当相乘的两个物理量含重复下标时,表示分量求和。比如公式
包含重复下标i,其实表达的是(对三维问题)
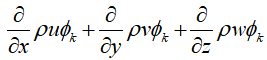
同样对于
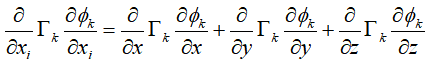
3.2 单一下标表示分量
这点很容易理解,比如N-S方程,可以用一个方程表达三个方向上的动量守恒。这里的表达主要是标量方程的个数。
3.3 梯度算子
梯度算子是倒三角,对标量▽f表示梯度,是矢量;对矢量▽*F表示散度,是标量。

似乎有点绕,但其实很好理解,可以认为梯度算子就是一个矢量,矢量乘以标量f=矢量;矢量点乘*矢量=标量
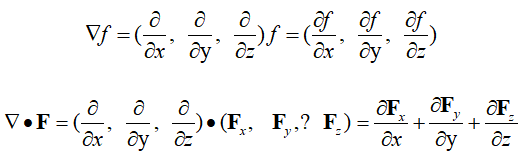
3.4 拉普拉斯算子Δ
拉普拉斯算子是正三角,为二阶微分算子,其实就是梯度的散度
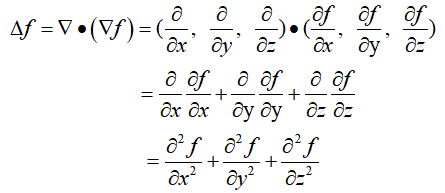
最终的结果就是二阶微分算子。
为什么会定义这两个算子??
对比输运方程我们会发现,对流项可以用梯度算子▽表示,扩散项可以用拉普拉斯算子Δ表示,当然也可也用梯度算子表示。
定义这两个算子之后,公式的表达就会很简明,同时对于不了解的人也很难理解。
比如我们用算子形式描述对流换热方程
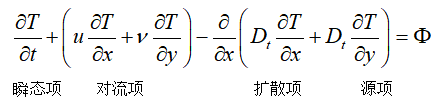
算子形式为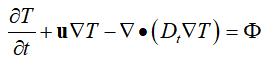
现在我们回过头来看Fluent提供的标准标量输运方程
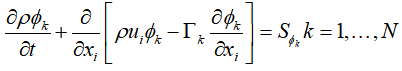
你能把它表示成我们熟悉的形式吗?
形式1:对于二维
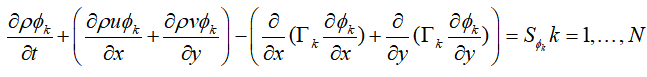
形式2:
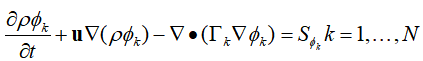
给大家一个传质方程,大家可以自己练习练习
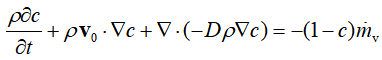
4. 标准输运方程
现在我们理解了Fluent UDS标准输运方程
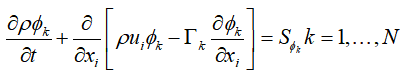
其中的Φk就表示待求的标量,比如温度T,组分浓度c,但这两个标量都是Fluent可以直接求解的,没必要通过UDS来求解。通常我们通过UDS来求解其他的标量,比如分压力、化学反应、电势等。
对于方程中的每一项,Fluent都存在默认的设置,实际上标准输运方程就是每一项的默认设置。
如果你的方程和标准输运方程形式上相同,那么你只需要打开UDS即可,不需要进行其他的设置
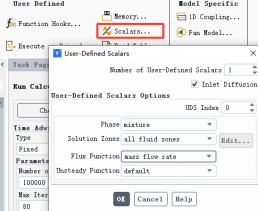
但上述情况是不可能的,如果保持完全一致,Fluent自带的模型就可以求解了。如果方程和标准输运方程有区别,Fluent对每一项都提供了相应的UDF来定义。

比如下面的方程
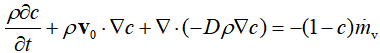
将其转换为标准形式后
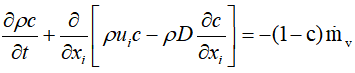
和标准形式对比
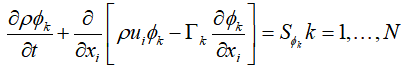
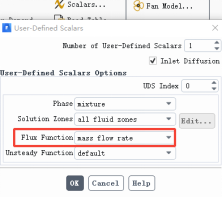
瞬态项和对流项完全相同,我们需要定义的只有扩散项和源项。
瞬态项加载位置
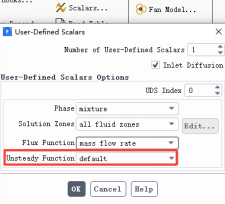
对流项加载位置
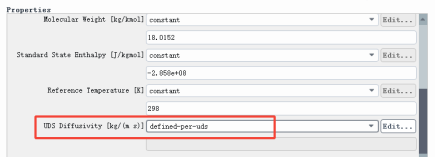
扩散项加载位置:材料物性设置界面
源项加载位置:Cell zone condition
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删