出现次数通常用于通过指定给定流动路径在多型腔工具中重复的次数,为填充+保压分析简化所需建模的数量。例如,对于一个自然平衡的8型腔工具,只需对一个零件和浇注系统建模。如果需要进行冷却、翘曲或应力分析,则不可使用出现次数来表示零件的一部分。必须将整个零件建模。
出现次数是一个有用的简便途径,可用于减少建模的次数和分析具有对称流动路径的模型所需的时间,尤其在多型腔模型中,仅需对一个型腔进行建模,其他相同的型腔可在分析中通过出现次数作为参考。定义相同的流动路径可使物理几何对称并使流经这些路径的塑料的体积相等。下图显示了一个自然平衡的8型腔工具。只需要为显示为红色的几何建模。
通过出现次数来分析其余型腔

自然平衡的8型腔工具中的出现次数。上图中的出现次数可按下述方式定义:主流道唯一,因此出现次数为1。主要流道出现次数为2,因为在主流道的底部,流动路径被分成2部分。辅助流道出现次数为4,流动路径其余部分的出现次数为8。
对称流动路径
在考虑使用出现次数对简单零件建模之前,了解““对称流动路径””的概念非常有用。当流动路径的物理几何对称且流经路径的塑料的体积相等时,流动路径可被认定为对称。下图显示了一个人工平衡的 8 型腔工具。此流道系统包括两个不同的流动路径(分别用红色和蓝色表示),因此出现次数与第一个示例不同。
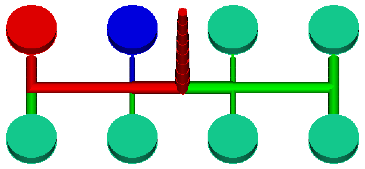
人工平衡的 8 型腔工具中的出现次数
上图中的出现次数可按下述方式定义:主流道(红色)是唯一的,因此出现次数为1,主要流道(红色)的出现次数为2,因为在主流道的底部,流动路径被分成2个部分。辅助流道、浇口和零件(用蓝色表示)的出现次数为4。
使用出现次数降低模型大小的原则
通过指定某条流动路径的重复次数,可使用出现次数降低分析所需的建模量。但如果要运行以下分析,则必须对零件进行完整建模,而不能使用出现次数:1冷却分析,2翘曲分析,3应力分析。
在考虑使用出现次数对简单零件进行建模之前,了解对称流动路径概念很有帮助。当流动路径的物理几何对称且流经路径的塑料的体积相等时,流动路径可被认定为对称。
零件和流道系统主要有 3 种组合:
1. 直接注射进型腔 (a)
2. 通过流道系统注射进多浇口型腔 (b)
3. 通过流道系统注射进多个型腔 (c)
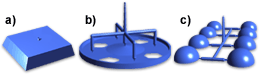
当然,除这三种基本组合之外还有许多其他组合方式,但为了简单起见,其他方式这里不做介绍。默认情况下,认为模型的所有表面和单元的出现次数都是1。