Matlab绘图与计算基础操作手册

基本绘图方法

subplot(121)与subplot(1,2,1)一个意思

二维图形

x=-pi:.1:pi;%步长为0.1
y1=sin(x);
y2=cos(x);
figure(1)
subplot(2,1,1)%确定在窗口建立2行1列的两个窗口
plot(x,y1,x,y2)%一个窗口画多个二维线性曲线
grid on 
title('plot(x,y1)')
subplot(2,1,2)
plot(x,y2)
xlabel('time')
ylabel('y')

注:
x轴和y轴的数据长度必须相同

结果为：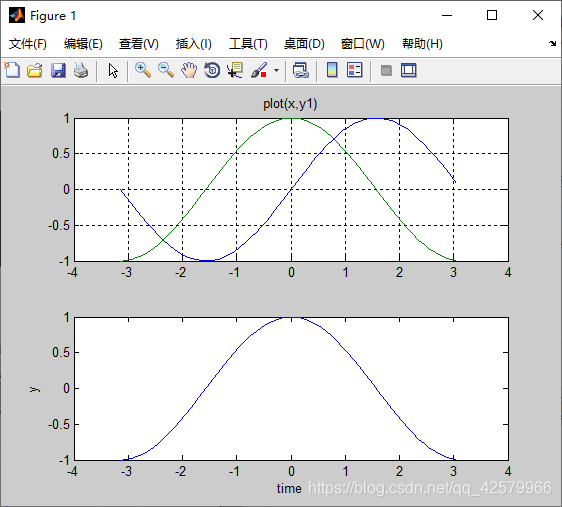

特殊二维曲线

• bar/barh:

%垂直条形状
y=[213,121,153,124,184,126,105,247,257,257,156,214,332,371,315,416,461]
subplot(121);%与subplot(1,2,1)一个意思
bar(y);%垂直条形状,横坐标自动为y值的个数
title('垂直等高线图')
axis square %将当前坐标系图形设置为方形,横轴及纵轴比例是1：1
%水平等高线
subplot(122);
barh(y);
title('水平等高线图')

结果为：

• 散点图

%散点图
theta=linspace(0,2*pi,300);
x=sin(theta)+0.75*rand(1,300);
y=cos(theta)+0.75*rand(1,300);
figure(1);
scatter(x,y)
axis square

注：

   y = linspace(x1,x2,n) 生成 n 个点。这些点的间距为 (x2-x1)/(n-1)

   而与theta=0:2*pi:300不同，此方法不足300个点

结果为：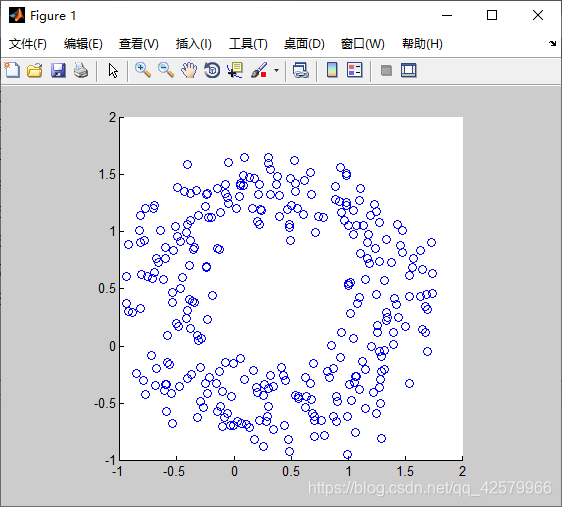

三维图形

空间曲线绘制

clc
x=0:.1:4*pi
y1=sin(x);
y2=cos(x);
plot3(x,y1,y2);
grid on

x ,y1,y2必须为大小相同的向量或矩阵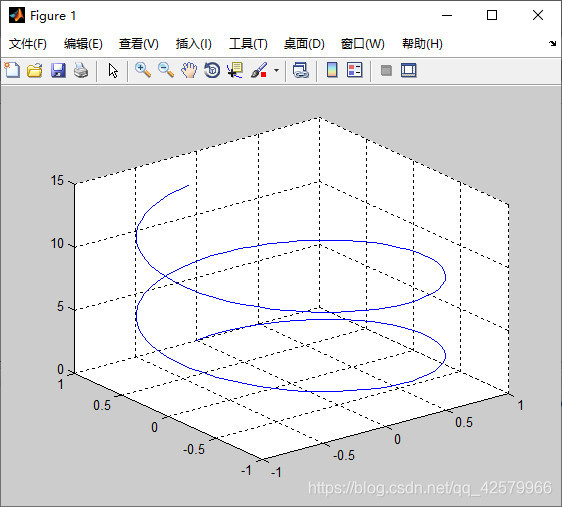

空间曲面绘制

三维曲面和三维曲线的区别是 它必须要先在xy平面建立网络坐标，每一个网络坐标和z坐标对应曲面上的一个点

   则网络坐标生成为：

 

clc
x=-2:0.2:2;
y=x;
[X,Y]=meshgrid(x,y);%生成(x,y)矩阵网络的
Z=X.*exp(-X.^2-Y.^2);
surf(Z)

MATLAB计算

符号计算基础

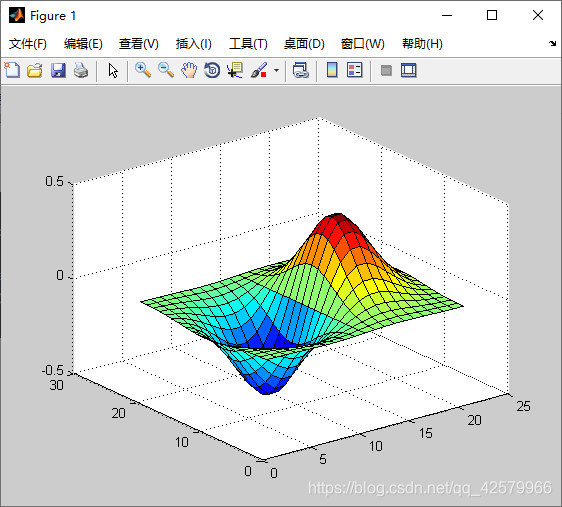
符号函数与普通函数区别：

普通函数：结果尽可能计算出来，然后用用浮点数（double）的形式表示
符号函数：都将以最接近原值的有理数形式或者是函数形式表示(方便我们观察)

sym:定义单个符号变量

   syms:定义多个符号变量

用法：

a=sym('x')
y=sym('x^2+2*x+1')
f=sym('[a,x;a+x,a-x]')
syms b c d

a =
x
y = 
x^2 + 2*x + 1
f =
 
[     a,     x]
[ a + x, a - x]

符号矩阵创建与运算

加 减 乘：

A=sym('[1 2 3;4 6 9;a b c]');
B=sym('[1/2,2/5,3/4;x y z;2 3 5]');
A+B
A-B
A*B %乘法是矩阵乘法

结果为：

ans =
 
[   3/2,  12/5,  15/4]
[ x + 4, y + 6, z + 9]
[ a + 2, b + 3, c + 5]
 
ans =
 
[   1/2,   8/5,   9/4]
[ 4 - x, 6 - y, 9 - z]
[ a - 2, b - 3, c - 5]
 
ans =
 
[      2*x + 13/2,          2*y + 47/5,          2*z + 63/4]
[        6*x + 20,         6*y + 143/5,            6*z + 48]
[ a/2 + 2*c + b*x, (2*a)/5 + 3*c + b*y, (3*a)/4 + 5*c + b*z]

行列式，特征值，逆矩阵，秩等

clear;clc;
syms x y;
A=[1 2;x y];
det(A)%行列式
inv(A)%逆矩阵
eig(A)%特征值
rank(A)%秩

结果为：

ans =
 
y - 2*x
 
 
ans =
 
[ -y/(2*x - y),  2/(2*x - y)]
[  x/(2*x - y), -1/(2*x - y)]
 
 
ans =
 
 y/2 - (y^2 - 2*y + 8*x + 1)^(1/2)/2 + 1/2
 y/2 + (y^2 - 2*y + 8*x + 1)^(1/2)/2 + 1/2
 
 
ans =
 
2

代数方程组求解

一些说明：

   线性方程组：未知量的次数只能是1

   非线性方程组：至少有一个未知量的次数为1以上

方程组求解有：符号求解 or 数值求解

   可以先符号求解，如果想要具体的数值解，用double类型进行转化即可。

1. 线性方程组
   用/ or \的方式：
   
       例子：x+2y=5;2x+3y=7 求x,y
   
       先把方程组写成矩阵的形式：
   
   
       即AX=B的形式。
   
       则X=A\B

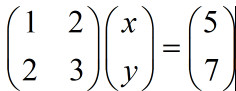
A=sym([1 2;2 3])
B=sym([5;7])
x=A\B
% 使用double将符号解转换为数值解
value_x=double(x)

x =
 
 -1
  3
value_x =

    -1
     3

1. 非线性方程组用solve: 用法： sol = solve(eq) sol = solve(eq, var) sol = solve(eq1, eq2, …, eqn) sol = solve(eq1, eq2, …, eqn, var1, var2, …, varn) eq为等式，var为变量 例子： 求解x,y

syms x y;
eq1=sym('a^2*x+b*y+c=0');
eq2=sym('x+y+a+b+c=0');
s=solve(eq1,eq2,x,y);
s.x
s.y

结果为：

ans =
 
-(a*b - c + b*c + b^2)/(- a^2 + b)
 
ans =
 
(a^2*b - c + a^2*c + a^3)/(- a^2 + b)

函数的极限及微积分运算

求函数极限

limit(f,x,a):f函数在x趋近于a时的极限

   limit(f,x,a,‘s’):s等于right为有极限，left为左极限

clear;clc;
x=sym('x');
y=sin(x)/(x^3+3*x);
a=limit(y,x,0)
b=limit(y,x,inf)%x趋近于无穷大

结果为：

a =
 
1/3
 
b =
 
0

求函数导数和jacobian矩阵

diff(f,v,n):f对v的n阶导数

   jacobian(f,v):多元向量f的Jacobian矩阵

   注：若f为矩阵，则对矩阵中的每个元素进行求导

clear;clc;
syms a x;
y=x^3+2*x^2+5*x+1
f=[3,2*x^2;a+2,x^a]
a=diff(y,x,1)
b=diff(f)%默认对x求一阶导

a =
 
3*x^2 + 4*x + 5
 
b =
 
[ 0,         4*x]
[ 0, a*x^(a - 1)]

求积分

不定积分：

   int(f,x):f对x进行积分

   定积分：

   int(f,x,a,b):f对x进行积分，上下限为（a,b）

注：若f为矩阵，则对矩阵中的每个元素进行求积分

clear;clc;
x=sym('x');
y=x+sin(x)/1+cos(x)
a=int(y)
b=int(y,x,0,1)

a =
 
sin(x) - cos(x) + x^2/2
 
b =
 
sin(1) - cos(1) + 3/2

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删