案例研究：利用Minitab缓解供应链中的“牛皮鞭效应”现象

背景

牛皮鞭效应(Bullwhip Effect)又称“牛鞭效应”或者“长鞭效应”，是经济学上的一个术语，指供应链上的一种需求变异放大现象。

1995年，宝洁公司(P&G)管理人员在考察婴儿一次性纸尿裤的订单分布规律时，发现一定地区的婴儿对该产品的消费比较稳定，零售商那里销售量的波动也不大，但厂家从经销商那里得到的订货量却出现大幅度波动，同一时期厂家向原材料供应商的订货量波动幅度更大。这一现象与人们在挥动鞭子时手腕稍稍用力，鞭梢就会出现的大幅度摆动的现象相类似。于是，人们就将这种现象称为牛皮鞭效应。

美国著名的供应链管理专家Hau L．Lee教授是最早将这种现象称为“Bullwhip Elfect”的，他解释Bullwhip Effect为：尽管特定产品的顾客需求变动不大，但是这些商品的库存和延期交货波动水平却相当大。简单地讲，牛皮鞭效应就是指供应链下游消费需求轻微变动而导致的上游企业生产、经营安排的剧烈波动的现象。当市场上一种商品的消费需求发生细微变动时，这种波动会沿着零售商、批发商、分销商直至制造商逆流而上，并逐级扩大，在达到最终源头供应商时，其获得的需求信息和实际消费市场中的顾客需求信息发生了很大的偏差，需求信息严重扭曲或失真，这就是牛皮鞭效应。

精明的供应链管理涉及利用渠道范围的整合来更好地满足客户需求。通过协调质量管理活动，可以提高生产力和效率。如果我们实施一种基于发散系统的控制技术，我们可能能够减少牛皮鞭效应，从而在单一的产品供应链中获得更多的控制。让我们更深入地研究如何确切地减少牛皮鞭效应。

第一步-从基本统计过程控制开始。

第二步-利用EWMA避免牛皮鞭效应。

第三步-采取行动，加快生产。

第一步-从基本统计过程控制开始

供应链对商业企业的健康至关重要，因此我们必须通过采取预防和紧急措施来维持供应链。由于供应链包含了如此多的方面，必须制定措施来指示供应链何时不能有效地和富有生产力地运行。幸运的是，基本的统计质量控制将指示供应链中何时存在风险。越快发现这些风险，就越能更好地进行必要的改变，以减少成本、瓶颈和库存短缺。一种常用且可信的统计过程控制技术是控制图。

控制图是监控过程特性的首选工具。控制图有多种类型，移动极差(I-MR)和均值极差(XBAR-R)图是最流行的两种类型。

现在让我们来看看实际操作中的控制图。在本例中，我们将查看一家公司，该公司希望仔细监控其某一产品的销售量。虚构的数据集由过去75天的销售量组成。

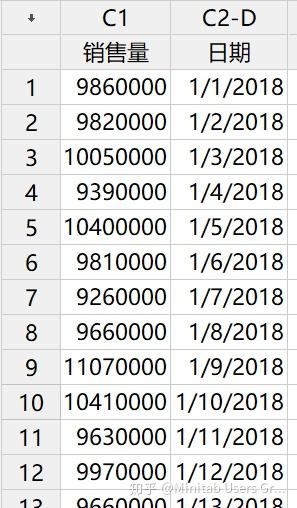
一旦数据集在Minitab统计软件中准备就绪，我们将点击：统计—控制图—单值的变量控制图—I-MR控制图。

我们将完成如下所示的对话框，然后单击“确定”。

然后我们会得到一个类似如下的控制图：

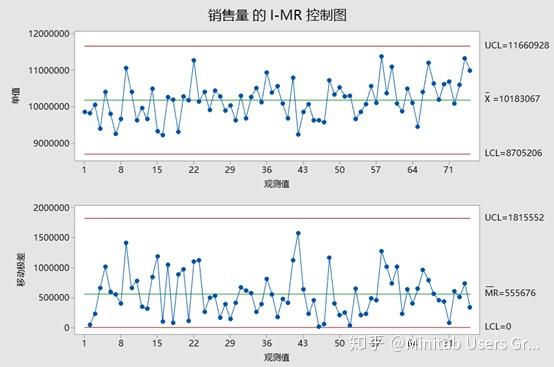
根据输出结果，我们得到了一个处于统计控制中的过程的控制图。这张图表没有指出任何失败的检验，也没有明显的模式。如果仔细观察，后面的数据显示过程均值可能略有上升，但没有正式脱离控制点的点位。如果该公司使用这张图表-而且只使用这张图表来监控供应链，他们会得出结论，平均水平随着时间的推移一直是稳定的。

在正常业务情况下，这应该足够了。然而，当商业环境发生变化时，就像今天一样，你必须更深入地研究数据，看看你是否能预测到即将到来的变化。

第二步-利用EWMA避免牛皮鞭效应

I-MR和XBAR-R控制图在检测过程均值变化较大的相关性方面是有效的，这就是为什么它们经常被用作统计过程控制的第一步。在正常的业务条件下，较小的波动没有那么大的意义，所以这些控制图就足够了。然而，当商业环境发生变化时，检测到流程中较小的变化对于供应链做好最好的准备是至关重要的。

指数加权移动平均（EWMA）控制图，不同于其他的控制图，它将所有以前的点的数据合并到后面的每个点上。因此，EWMA控制图能更有效地检测过程均值中的小变化。对感兴趣的质量特性的小变化的快速检测和易于计算使EWMA图表成为监控供应链的一个有吸引力的图表。这一点尤其重要，因为为了尽量减少牛皮鞭效应，我们需要在需要时尽可能迅速和明智地采取措施。

让我们看一下与前面相同的例子，但是使用EWMA控制图。工程师会决定使用它，以确保即使检测到一个小的变化。这可能有助于预测未来的牛皮鞭效应，让供应链提前做好准备。

要在Minitab中创建EWMA控制图，请转到统计>控制图>时间加权控制图> EWMA。完成如下所示的对话框，然后单击ok。

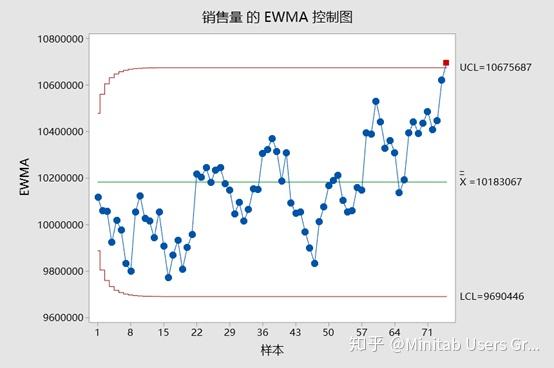
如你所见，3月5日以后，有一个明显的上升趋势，最后一点是失控的(用红色标记)。在这一点上，这种平均值的变化应该进行调查，因为销售的平均数量在增加，公司可能需要采取措施来满足客户的需求。

随着需求的增长，公司计划迅速增加生产。

第三步——采取行动，加大生产

随着EWMA控制图显示需求即将增加，公司可能会决定增加更多的生产线来满足不断增长的需求。当然，首先要看的是生产该产品的同一家工厂。

鉴于当前的事件，让我们用一个洗手液的例子。在这种情况下，该公司在两条生产线上生产洗手液，幸运的是，他们有第三条生产线，他们可以准备扩大生产能力。

在开始使用第三条线路之前，他们的工程师要确保两件事:

1) 所生产的洗手液酒精含量不低于60%

2) 第三条线和其他两条线的平均值是一样的

最终的目标是让这三条生产线生产出平均酒精含量为60%的优质产品。为了达到这一目的，该公司的一位统计学家建议对产品的酒精含量进行单因子方差分析(ANOVA)。

单因子方差分析是统计学中最常用的方法之一。这是用来确定因子在多个水平上的均值是否在统计上不同。该方法是双样本t检验的推广。但与t检验不同的是，单因子方差分析允许你在保证总体错误率的情况下检验2个以上的平均值。

回顾我们的示例，我们将两条生产线称为生产线1和生产线2。该公司想知道第三生产线（生产线3）生产的产品平均水平与生产线1和生产线2相似。经过功效和样本量分析后，他们决定从每条生产线中测量25瓶洗手液，共计75瓶洗手液。数据已放入Minitab工作表中。

单因子方差分析检验以下假设：

H0：所有均值都相等

H1：并非所有均值都相等

检验的决定将是拒绝还是不拒绝原假设。如果我们拒绝原假设（H0），那么我们可以说至少其中一条线平均值不同（然后，我们将不得不进行多重比较分析以找出哪些线不同）。如果我们不能拒绝，我们得到的结论是3条生产线的均值没有显著差异。

要在Minitab中进行单因子方差分析，请转到：统计 > 方差分析 > 单因子方差分析。完成如下所示的对话框。单击“图形”并选择“箱形图”，然后单击OK两次。

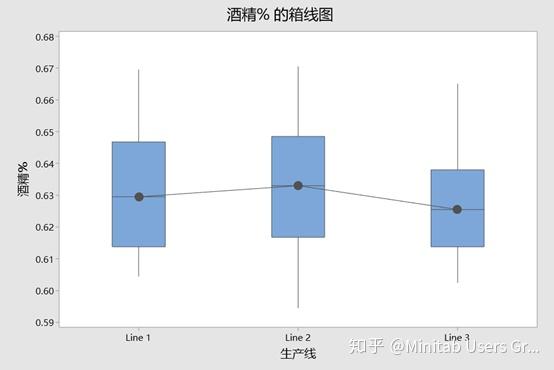
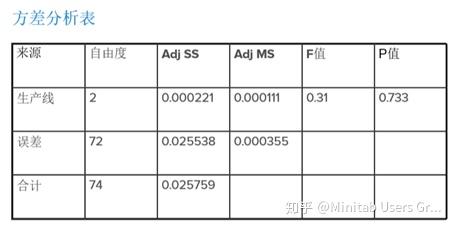
分析的输出如下。箱形图显示这些线的均值并没有那么大的不同。此外，3条生产线的平均值都高于目标平均值0.6，这表明每行生产的瓶中至少含有60%的酒精。

方差分析表中的p值为p = 0.733。使用0.05的alpha值，我们可以得出95%置信区间的结论，没有足够的证据表明这3条生产线线的平均值是不同的。换句话说，因为没有证据表明这三条线是不同的，所以公司不能拒绝原假设，并假设这三条线的平均值是相似的。于是，该公司可以使用第三生产线生产额外的洗手液!

结论

无论您是处于数据分析和统计过程控制的早期阶段，还是正在寻找更高级的方法，Minitab都可以帮助您快速有效地分析数据，以便轻松有效地采取数据驱动的操作。

如果您已经在使用控制图，那么现在也许是探索EWMA控制图以更快地识别变化的时候了。然后，您可以进一步利用数据分析来帮助您提高最需要的产品的产量。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删