函数——是编程的核心概念之一,是能够完成相对独立功能的代码封装成的模块。
在主程序中通过函数名和实参调用它,通过接口(即函数的输入、输出参数)来实现“通讯”。所以在调用函数时,你只要知道“被调用的函数是用来做什么的”,以及“如何对应它的输入、输出参数”就行了。
关于形参(形式参数)和实参(实际参数):函数定义中的参数就是形参,只是用来限定函数所接收的数据类型的,“泛指该数据类型下任一元素”;函数调用中的参数就是实参,是“特指的具体数值”来代入函数体执行代码。例如(C语言):
int max(int x, int y)
{ if (x >= y)
return x;
else
return y; }
……
int a = 5, b = 4;
max(2,3);
max(a,b);
……
其中,x,y是形参,2, 3,a, b是实参。
使用函数的好处:增加程序的可读性(函数可独立放在主程序之外)和重用性(一个函数可以多次被调用)。
Matlab的自定义函数,常用的有:m文件定义函数、inline(内联)函数、匿名函数。
1. Matlab函数的基本结构
function[输出形参表: output1, ...,outptn] = 函数名(输入形参表: input1, ... , inputn)
注释说明部分
函数体代码部分
end说明:function:表示编写的是一个函数;
输出形参表,即函数的返回值,各返回值间用逗号隔开;(不需要像C语言那样,通过return到返回值来赋值,outp_args相应的参数可以直接使用)
函数名:需要和m文件名保持一致
输入形参列表:即函数的各输入参数,用逗号隔开;
函数体:完成函数的具体功能,是根据具体需要编写的;通过使用“函数的输入参数”、“自定义变量”、“流程控制结构”来实现;
end:表示此函数结束,也可省略。
2. 函数调用
定义完的函数保存为同函数名的m文件,放置在Matlab的当前路径之下(或修改当前路径为m-函数文件所在路径),然后就和使用Matlab自带的函数一样,直接在命令窗口或程序代码中使用该函数就是调用它了。调用函数时,只需要知道函数是完成什么功能的,以及它的输入参数、输出参数。
函数调用的一般格式为:
[输出实参表]=函数名(输入实参表)
注1:函数中遇return语句时,将退出函数体,此函数调用结束;
注2:函数体里面也可以定义一个或几个函数,称为子函数;注意:子函数只能存在于主函数体内,不独立存在;子函数在主函数体内的位置可以任意,不影响使用;子函数只能被主函数以及其他位于同一主函数体下的子函数调用,但子函数“句柄”例外;
注3:在调用函数时,Matlab用两个永久变量nargin和nargout分别记录调用该函数时的输入实参和输出实参的个数。只要在函数文件中包含这两个变量,就可以准确地知道该函数文件被调用时的输入输出参数个数,从而决定函数如何进行处理。
例1 函数(子函数)定义与调用示例,求向量的最大、最小值。
编写m-函数文件:max_min_values.m
function [max,min] = max_min_values(X)
%输入参数X为数值向量,返回其最大值和最小值
max=mysubfun1(X);
min=mysubfun2(X);
function r=mysubfun1(X) %子函数1
x1=sort(X, 'descend');
r=x1(1);
end
function r=mysubfun2(X) %子函数2
x1=sort(X);
r=x1(1);
end
end
调用函数(命令窗口):
A = [34,56,23,11,2,39];
[m,n]=max_min_values(A)
运行结果: m = 56
n = 2
可以让用户编写简单的函数而不需要创建M文件。语法格式:
f=inline('函数表达式', '变量1', '变量2', ……)
调用方式:y=f(实参列表)
注意:实参列表顺序应与inline()定义中形参列表的顺序一致。
这种函数定义方式是将它作为一个内部函数调用。好处是,它是基于Matlab的数值运算内核的,所以它的运算速度较快,程序效率更高。缺点是,该方法只能对数值进行代入,不支持符号代入,且对定义后的函数不能进行求导等符号运算。
内联函数示例:
f=inline('x^2+y','x','y')
z=f(2,3)
运行结果: f = Inline function: f(x,y) = x^2 + y
z = 7
1.匿名函数基本语法
匿名函数具有内联的所有优点,并且效率比更高。匿名函数的主要功能是:
(1)可以代替“将函数编写为单独的m-文件”;
(2)可以实现符号函数的赋值运算;
(3)很方便地对含参变量函数进行操作。
基本格式:
f=@(参数1, 参数2, …) 函数表达式
其中,@为句柄操作符,可以定义指向函数的句柄,函数句柄,可以理解成函数的“代号”,适用于函数名比较长,用“代号”代替函数操作更方便。
匿名函数示例:
f=@(x,y)x^2+y^2;
f(2,3)
a=1:5;
b=5:-1:1;
c=0.1:0.1:0.5;
g=@(x,y)x.^2+y.^2+c;
g(a,b)
运行结果: ans = 13
ans = 26.1000 20.2000 18.3000 20.4000 26.5000
也可以定义二重匿名函数:例如,
f=@(a, b) @(x) a*x+b;
其中,“a, b”是外层变量,“x”是内层变量。
这样理解:每个“@”符号后面括号里的变量的作用域一直到表达式的结尾。例如对于“a=2, b=3”, f(2, 3)是以x为变量的匿名函数:
(f(2, 3))(x)=2*x+3
类似的可以定义多重匿名函数。
2. 匿名函数的应用
(1) 求解参数方程
例2 对带参数a的参数方程: e^x+x^a+x^{\sqrt{x}}=100e^x+x^a+x^{\sqrt{x}}=100
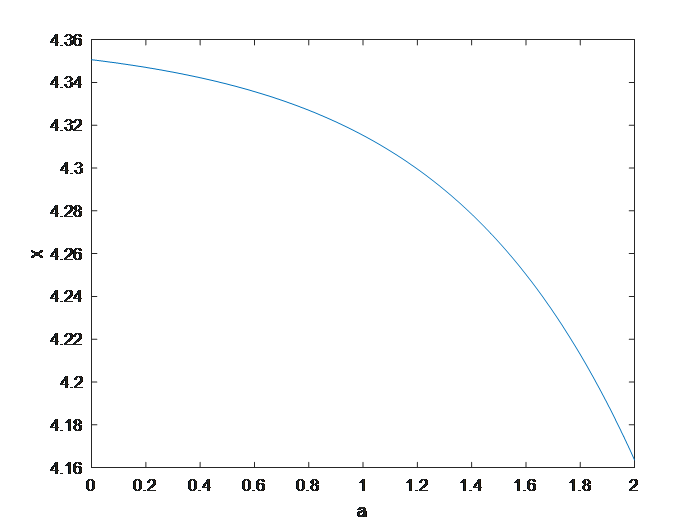
要求针对a在[0,2]上的不同取值求解方程,并绘制方程的解x与a的关系的图像。
代码:
f=@(a) @(x) exp(x)+x^a+x^(sqrt(x))-100;
%相当于(f(a))(x)=exp(x)+x^a+x^(sqrt(x))-100
format long
fzero(f(1),4) % a=1时,求解方程的根x,初始值为4
A=0:0.01:2;
x=@(a) fzero(f(a),4); %带着参数a求解方程的根x,得到x=x(a)
X=@(A) arrayfun(@(a) x(a),A);
% x(a)只能接受标量a,处理成能接受向量A
Y=X(A);
plot(A,Y)
xlabel('a')
ylabel('x')
运行结果:ans = 4.315274301739397
注:f(x)只能接受标量的自变量x,arrayfun函数对f做向量化处理使得f作用到向量自变量X上得到F(X). 语法:
F=arrayfun(f, X)
相当于用f作用到向量X的每个分量上。示例:
f=@(x) 2*x; %f(x)=2*x
F=@(X) arrayfun(f,X); %F(X)=2*X
F(1:4)
输出:ans = 2 4 6 8
(2) “显式”表示隐函数
隐函数一般无法给出显式表达式,但借助匿名函数和求根函数fzero()可以实现“已知隐函数表达式,对于给定的自变量x,通过数值方法求出因变量y”。
例4 “显式”表示下列隐函数: z=\sin\big((zx-0.5)^2+2xy^2-\frac{z}{10}\big)\exp\Big\{-\big[x-0.5-\exp(-y+z)\big]^2+y^2-\frac{z}{5}+3 \Big\}z=\sin\big((zx-0.5)^2+2xy^2-\frac{z}{10}\big)\exp\Big\{-\big[x-0.5-\exp(-y+z)\big]^2+y^2-\frac{z}{5}+3 \Big\}
其“显式表示”为:
z=@(x,y) fzero(@(z) z-sin((z*x-0.5)^2+2*x*y^2-z/10) *exp(-((x-0.5-exp(-y+z))^2+y^2-z/5+3)),rand)
相当于求解满足该隐函数方程的z=z(x,y), 其中rand生成随机数作为初始值。
代码:
z=@(x,y) fzero(@(z) z-sin((z*x-0.5)^2+2*x*y^2-z/10) *exp(-((x-0.5-exp(-y+z))^2+y^2-z/5+3)),rand);
z(2,0.5) %求x=2, y=0.5时的z值
%绘制z(x,y)的图像
[X,Y]=meshgrid(-1:0.1:7,-2:0.1:2);
Z=arrayfun(@(x,y) z(x,y),X,Y);
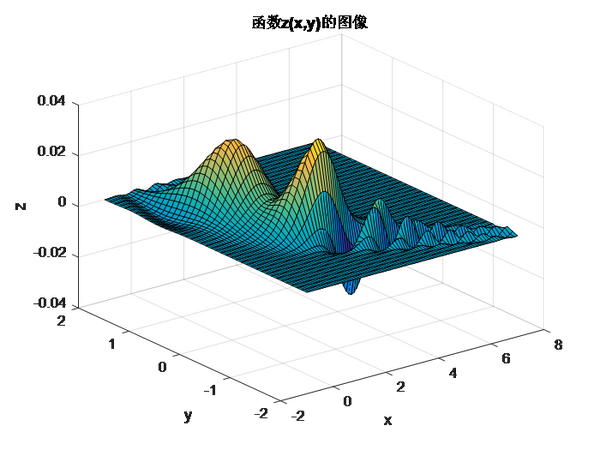
surf(X,Y,Z)
xlabel('x')
ylabel('y')
zlabel('z')
title('函数z(x,y)的图像')
运行结果:ans = 0.016721201334182
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删