1.      伤害计算公式

伤害=攻击*爆伤（满暴击前提下）

2.      提出问题：如何利用经济学原理，科学的分配这三种属性，使伤害最大化

3.      提出假设：在24号位都为攻击加成的前提下，根据六号位的选择，分别计算其伤害受暴击，暴击伤害，攻击加成的影响

4.      流程：

列出伤害函数，利用matlab画出“伤害”这个数值受3个变量影响的3维图像，分析得出结论

关于御魂的知识：

2，4，6号位的主属性，攻击加成55%，暴击55%，爆伤89%固定；副属性，4条为“不缺腿”，暴击，速度，攻击加成等数值每一阶段随机在2.4~3.0之间；暴击伤害随机在3.2~4.0之间。升到15级有5次提升，加上初始的那次，相当于6次，但初始那次是固定的，6个位置，有效次数（在此，没有计算小攻击，仅认为攻击加成，暴击，暴击伤害对其影响，有利于计算的进行）共有（3+5）*6=48次，其中固定属性3*6=18次，由概率支配的次数是5*6=30次。每号位置上有5次提升机会，所以6个位置一共有496组可能

分析计算：

1.      设48次中，攻击加成占a次，【6~36】；暴击占b次，【6~42-a】暴击伤害为48-a-b次

根据每次提升的数值期望，暴击和攻击加成为2.7，暴击伤害为3.6

设弑神面板攻击为k=3300，最终伤害为F，面板暴击为10，一号位小攻击486

2.

6号位为暴击时：F=【k（2.1+2.7a/100）+486】*（1.5+3.6c/100）*【（10+55+2.7b）/100】

6号位为攻击加成时：F=【k（2.1+0.55+2.7a/100）+486】*（1.5+3.6c/100）*【（10+2.7b）/100】

6号位为暴击伤害时：F=【k（2.1+2.7a/100）+486】*（1.5+0.89+3.6c/100）*【（10+2.7b）/100】

公式的三部分，是  攻击*暴击伤害*暴击概率  ，所以不同于其他满暴击是计算攻击加成和暴击伤害对最终伤害的影响，这个公式可以更加全面的阐释这三个属性对伤害的贡献。

如果想要计算后者那种情况，就相当于给暴击副属性一个定量，函数的次数减一次，更加简单。

3.化简公式，在matlab中计算，并画出3维图像，x轴攻击加成，y轴暴击伤害，z轴最终伤害（由于维度的限制，可视化上只能选出这两个代表性的）

4.结果：

6号为暴击：

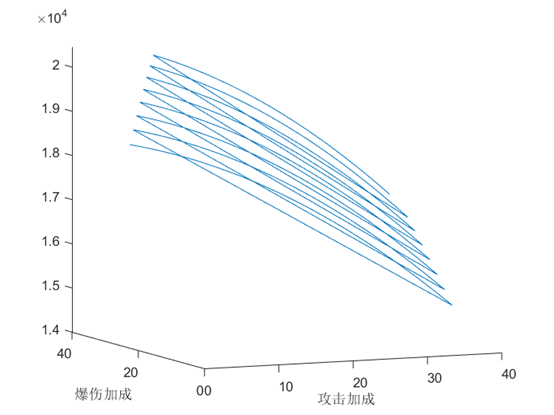
   这个形状优点像指尖薯角
 

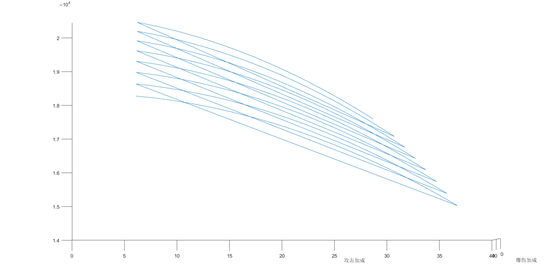
   攻击加成和伤害的关系
 

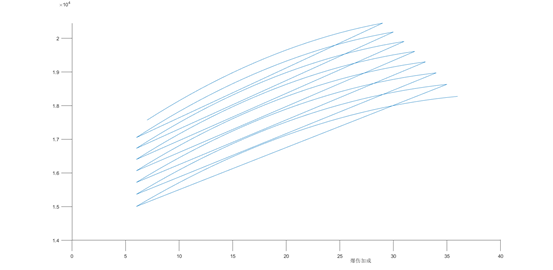
   爆伤和伤害的关系
 

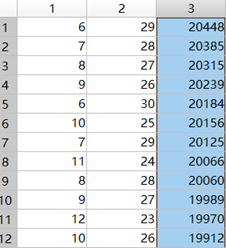
   6号暴击时，最高伤害的几种搭配
 

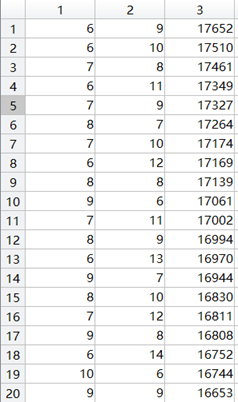
第一列是攻击加成，第二轮是爆伤，第三列是最终伤害。

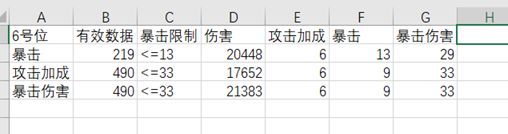
可以看出，6号味为暴击时，极限伤害为20448，这是攻击加成6次，爆伤29次，暴击13次。简单的说，就是暴击先满，然后全堆爆伤；

这组数据从496组数据中剔除暴击超过100的数据，有效数据219组

6号位攻击加成：

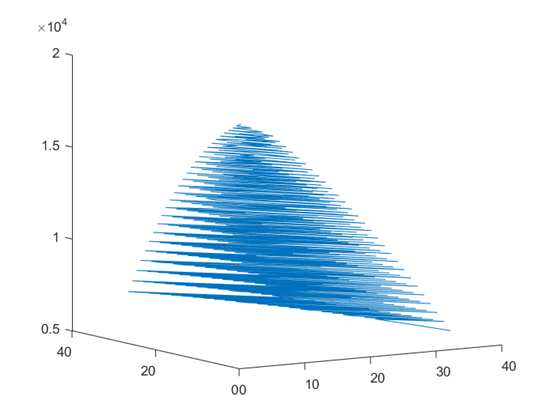
   和第一钟情况类似，数据变多了
 

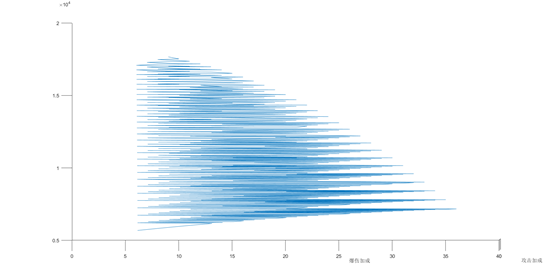
   爆伤和伤害的关系
 

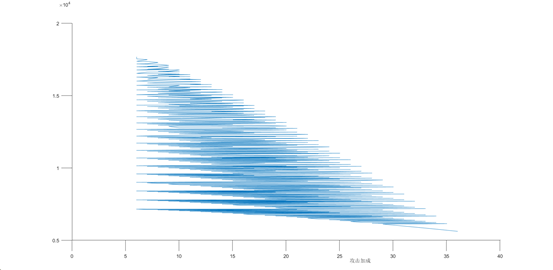
   攻击加成和爆伤的关系
 

   明显伤害低了很多
 

有效数据490组，最高伤害17652，攻击加成6次，暴击伤害9次，暴击33次

可以看出，6号位攻击加成，伤害上限很低，暴击依然是最高依赖对象

6号位暴击伤害：

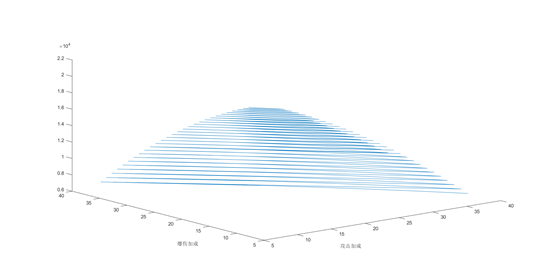
   和之前的差不多
 

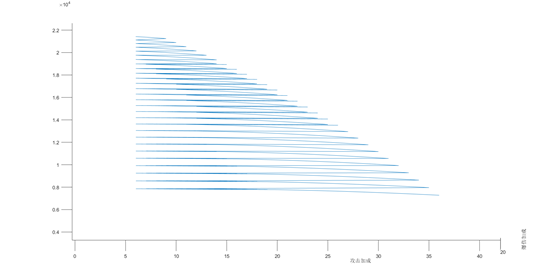
   攻击加成和伤害的影响
 

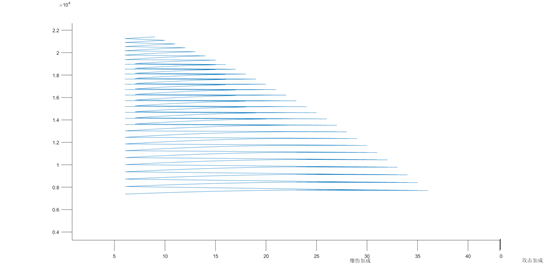
   爆伤和伤害影响
 

有效数据490组，最高伤害21383，攻击加成6次，暴击伤害9次，暴击33次

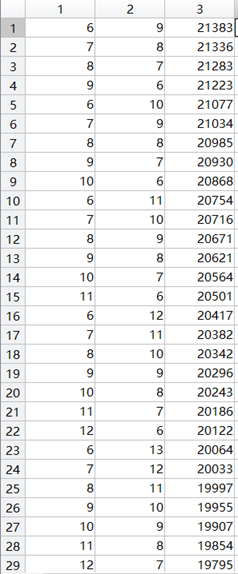
   看看这组数据
 

1~4行，攻击次数+爆伤次数=15，随着爆伤次数降低伤害递减

5~9行，攻击次数+爆伤次数=16，随着爆伤次数降低伤害递减

10~15行，攻击次数+爆伤次数=17，随着爆伤次数降低伤害递减

16~22行，攻击次数+爆伤次数=18，随着爆伤次数降低伤害递减

   总结
 

总结：

1.      无论6号味为什么属性，暴击对伤害的贡献最高，其次是爆伤，最后是攻击加成

2.      三种情况下伤害极限的排名：暴击伤害>暴击>攻击加成，就是说，你六号位戴攻击加成不如戴暴击，只要你副属性爆伤多

3.      三种情况，都是在满暴时，伤害的极限期望最高

注意：

1.      本实验极限数据较低，因为以下因素：

（1）      没有考虑御魂2，4件套装的影响，但毫无疑问，2件套暴击要比攻击加成划算

（2）      本实验前提是2，4号位置为攻击加成，还没测试2号速度时的数据

（3）      弑神面包为攻击3300，暴击10，初始爆伤150

（4）      御魂不是极限御魂，是期望值

写在最后：本文只是个人思路观点，不一定正确

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删