岩石爆破理论及LS-DYNA数值模拟方法

岩石在爆破荷载作用下表现的性质十分复杂，在实际的钻爆开挖中容易引发安全事故。埋入岩体中的炸药发生化学爆炸后，岩石将在爆炸近区发生压剪破坏形成粉碎区，在爆炸远区发生张拉破坏形成裂隙区。非线性动力分析有限元软件LS-DYNA以其高效、准确等优点被广泛应用于爆破、冲击等领域。对于岩石爆破这类大变形问题，其中的ALE算法能有效避免因网格畸变而导致的计算难题。它结合了Lagrange算法与Euler算法的优点，可用于解决流体-固体耦合问题。

本人针对各种工况下的爆破方法录制了大量视频课程，如对爆破数值模拟感兴趣的朋友可以购买学习。

1.1 岩石爆破理论

1.1.1 无限域岩石的爆破

现有的爆破理论认为，埋入无限岩石中的炸药发生化学爆炸后，将在岩石中形成以装药为中心由近及远的不同程度的破坏区域，依次称为粉碎区、裂隙区和弹性震动区，如图1所示。

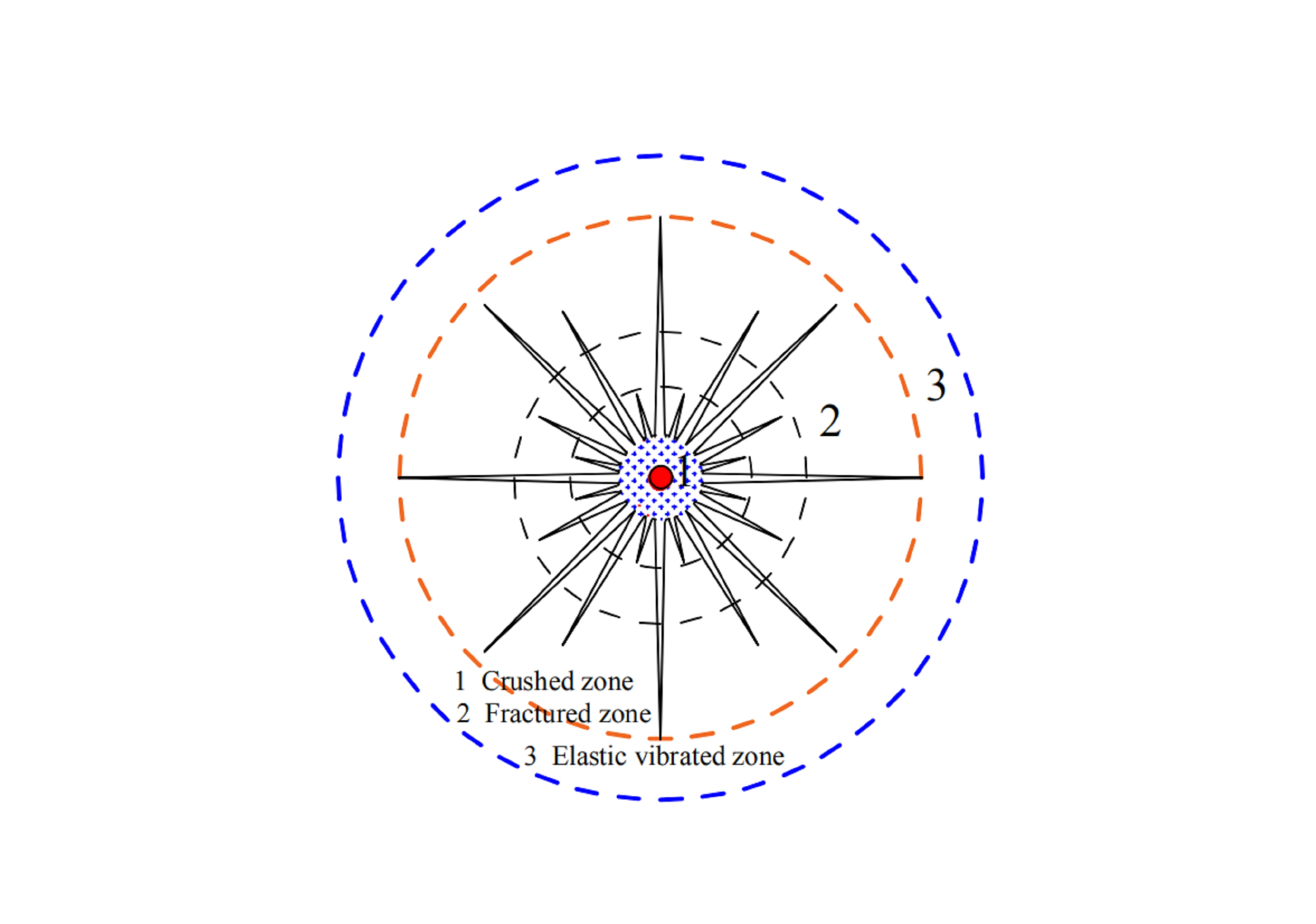
图1 无限域岩石单孔爆破

Fig 1 Single hole blasting of infinite field rock

岩石在粉碎区内受到的爆炸载荷加载率最高，该处应力波的强度远大于岩石的动态抗压强度，因此岩石发生粉碎性破坏并形成空腔。另外，粉碎区距离炸药较近，还会受到爆炸气体的高温高压作用。随着爆炸应力波向远处传播，应力波强度逐渐减小，当其强度小于岩石动态抗压强度后，岩石内将不再形成粉碎区。然后，岩石径向受压时会伴随有环向拉应力，由于岩石的动态抗拉强度远小于其动态抗压强度，因而岩石会在环向拉应力的作用下发生张拉破坏，并形成径向拉伸裂纹。在裂隙区外，随着应力波继续衰减，此时岩石中不再出现明显的破坏，可认为该区域的岩石只产生了弹性震动，因而称为弹性震动区。

具体实现过程可参考本人课程《（SCI）LS-DYNA的岩石单孔及双孔爆破裂纹扩展模拟》和《LS-DYNA的三维岩石爆破裂纹扩展模拟》。

1.1.2 临自由面岩石的爆破

如前所述，埋入无限岩石中的炸药爆炸后，将在岩石中依次形成粉碎区、裂隙区和弹性震动区。当埋入岩石中的炸药临近自由面时，爆炸应力波会在自由面附近发生反射作用。此时，径向压缩波会在自由面处反射为径向拉伸波，使得自由面附近的岩石内萌生更多的环向拉伸裂纹。而根据炸药到岩石自由面距离的不同，还会在自由表面附近引起岩石的破裂、鼓包和抛掷，进一步形成漏斗状的炸坑，称为爆破漏斗。

具体实现过程可参考本人课程《LS-DYNA岩石爆破漏斗模拟》和《LS-DYNA的三维爆破SPH-FEM耦合法》。

1.2 LS-DYNA软件介绍

1976年，美国Lawrence Livermore实验室的John Hallquist博士发布了最早的DYNA软件。20世纪80年代，该软件被法国ESI公司商品化。1989年，John Hallquist博士开始经营自己的公司Livermore Software Technology Corporation(LSTC)，并推广了如今的DYNA软件版本：LS-DYNA。

在此之后，LS-DYNA陆续推出了930版、936版、940版、950版、960版和970版，并且ANSYS公司已收购了LS-DYNA软件的使用权。如今，LS-DYNA软件已是一款功能强大的几何非线性（大位移、大转动和大应变）、材料非线性（140多种材料动态模型）以及摩擦和接触分离等界面状态的非线性程序。它以Lagrange算法为主，兼有ALE和Euler算法；以显式求解为主，兼有隐式求解功能；以结构分析为主，兼有热分析和流固耦合功能；以非线性动力分析为主，兼有静力分析功能。综合来看，它是一款军用和民用相结合的通用结构分析非线性有限元程序。

LS-DYNA显示动力分析采用了中心差分法，结构系统各节点在第n个时间步结束时刻tn的加速度向量为：

                                                                                       (2)

式中：P为第n个时间步结束时刻结构上所施加的节点外力向量；Fint为tn时刻的内力矢量，表达式为：

                                                                                   (3)

式中：右边三项依次为单元应力场等效节点力、沙漏阻力和接触力矢量。

根据中心差分法的基本思路，加速度可由速度的一阶中心差分求出，而速度可由位移的一阶中心差分计算得到。因而有如下表达式：

                                                             (4)

                                                                                   (5)

因此，节点速度向量可由程序计算出的加速度结合差分公式表示，而节点位移向量可由节点速度向量结合差分公式表示，即：

                                                                   (6)

                                                                                         (7)

新的几何构型由初始构型x0和位移增量u相加得到，即：

                                                                                                          (8)

为了保证数值计算过程中的稳定性，应当满足自由度解在若干时间步后仍是有限值。通过理论分析可知，保证数值计算稳定的临界时间步长应满足：

                                                                                                         (9)

式中：ωn为系统中各单元的最高阶固有振动频率，一般由系统中的最小单元决定。系统中最小单元的振动特征值方程为：

                                                                                                         (10)

由式(10)可计算出的最大特征值即为临界时间步长中的各单元最高阶固有振动频率。为了保证数值计算时的收敛，LS-DYNA程序采用了变步长积分法，每时刻的积分步长由当前构形网格中的最小单元来确定。而在具体的计算中，还可在LS-DYNA程序的默认时间步长前乘一个小于1的时间步调整系数。

1.3 爆破数值模拟方法

为避免孔壁周围的岩石单元发生大变形而出现负体积的错误，采用流固耦合方法。另外，岩体的预应力和重复爆破过程分别由Dynain文件和完全重启动技术实现。

1.3.1 流固耦合方法

在LS-DYNA软件中主要有四种数值方法模拟岩石爆破过程，包括共节点方法、接触方法、施加爆炸应力波荷载方法和流固耦合方法。具体实现过程如下：

（1）共节点方法

岩石和炸药在建模时采用共节点，如图2所示。该方法的计算速度很快，但缺点也非常明显，即炸药单元的畸变会引起岩石单元也产生较大的变形，同时由于采用了共节点，炸药单元的滑移变形会受到限制，进而引起附加的虚假滑移刚度，会对计算精度产生影响。

图2 共节点方法

Fig 2 Common node method

（2）接触方法

岩石与炸药分开建模，并在两个部件之间设置侵蚀接触或滑移接触，如图3所示。该方法存在的问题是炸药单元会产生较大变形，容易出现求解过程突然终止且不报错的现象，并且网格畸变也会对计算精度产生很大的影响。另外，接触的设置有可能导致计算不收敛。该方法往往需要借助小型重启动技术，在炸药爆炸过程基本完成后通过*DELETE_PART关键字删除炸药PART，并使用小型重启动继续计算。

图3 接触方法

Fig 3 Contact method

（3）施加爆炸应力波荷载方法

该方法不需要建立炸药模型，只需建立岩石模型即可。典型的爆炸应力波荷载曲线如图4所示，可以根据荷载峰值和加载持续时间描述不同药量和爆速的炸药。该方法计算效率较大，但最明显的缺点是无法描述高温高压的爆炸气体作用于孔壁的过程和爆生气体促进裂纹扩展的准静态作用。

具体实现过程可参考本人发布的课程《LS-DYNA施加爆炸应力波曲线法模拟岩石爆破裂纹扩展》。

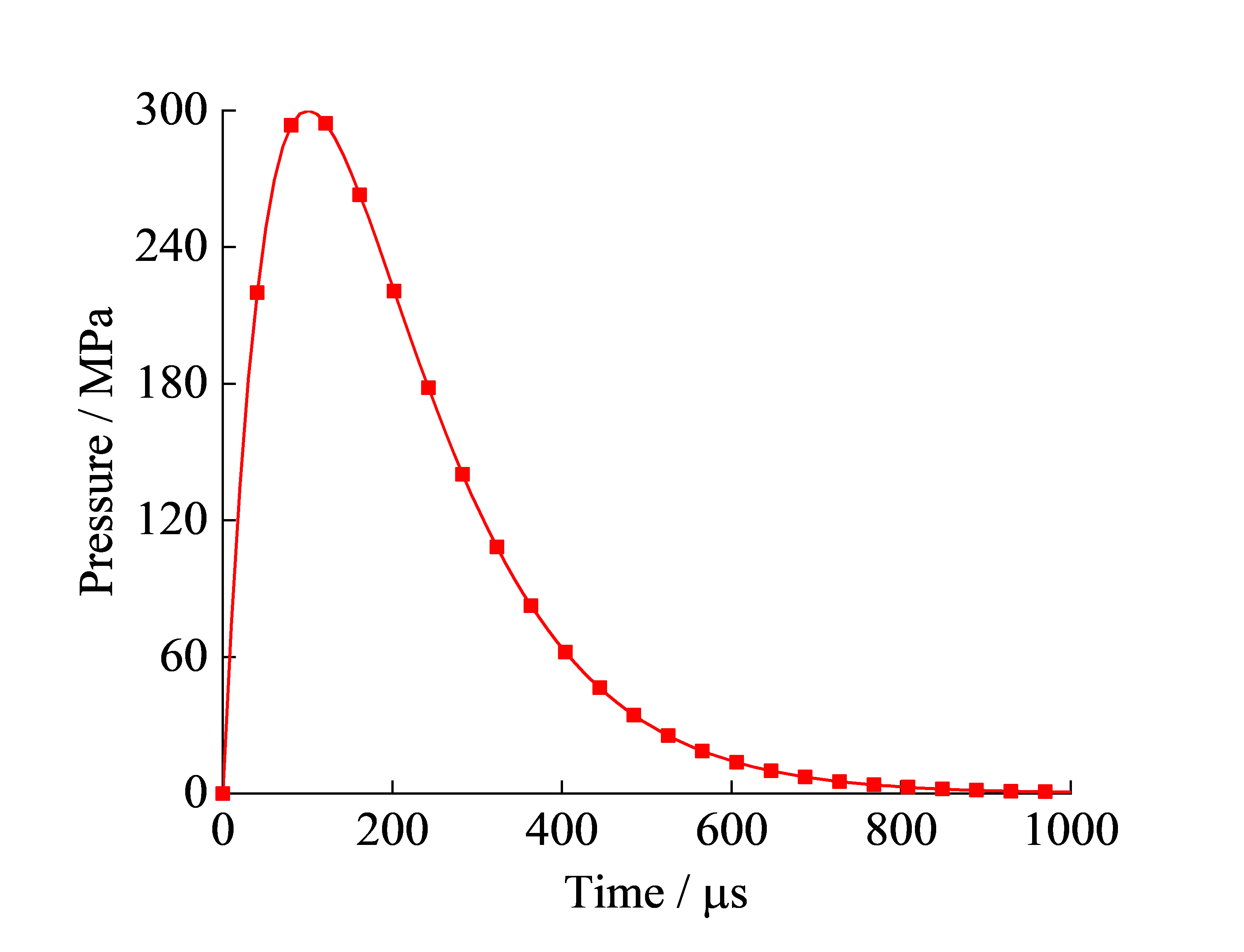
图4 爆炸应力波荷载曲线

Fig 4 Load curve of explosion stress wave

图5 流固耦合方法

Fig 5 Fluid-structure coupling method

（4）流固耦合方法

岩石采用Lagrange算法，空气和炸药采用ALE或Euler算法，并通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字实现流固耦合，如图5所示。其中，Lagrange算法的单元作为从面，ALE或Euler算法的单元作为主面。在前处理建模时，岩石应和空气、炸药采用分离式建模，而空气和炸药之间采用共节点建模，并将空气和炸药放在同一个ALE组里。需注意的是，应在炮孔周围设置更大范围的空气PART，这部分空气单元应与岩石单元相互重合，作为耦合域。

该方法能有效避免因网格畸变而导致的计算难题，大大提高了计算精度，被广泛应用于岩石爆破和冲击领域。本人发布的大多数课程均采用流固耦合方法。

1.3.2 预应力岩体爆破模拟方法

由于深部岩体处在预应力的状态下，其围压的施加属于静力分析范畴，而爆炸是超动态过程，属于动力分析范畴。因此，这两个步骤需要分开进行求解。目前，岩石地应力的施加主要有三种方法：动力松弛法、Dynain文件法和显隐式序列法。其中，Dynain文件法兼具准确、高效和操作方便等优点。该方法的主要分析过程如下：

（1）建立爆破数值模型，并输出原始K文件；

（2）基于原始K文件，将空气、炸药和堵塞PART删除，定义围压载荷曲并施加于岩石模型外边界，并通过*INTERFACE_SPRINGBACK_LSDYNA关键字输出包含岩石应力状态的Dynain文件，进而将该K文件递交求解，完成静力分析过程；

（3）基于原始K文件，将岩石PART删除，并通过*INCLUDE关键字将预应力岩石模型导入，最后将该K文件递交求解，完成动力分析过程。

具体实现过程可参考本人发布的课程《LS-DYNA地应力下的隧道爆破三维模拟》和《（SCI复现）LS-DYNA地应力掏槽爆破》。

1.3.3 重启动模拟方法

对于岩石循环或重复起爆问题，需要借助重启动技术进行分析。在LS-DYNA软件中，重启动分析主要分为以下三种类型：

（1）简单重启动

当求解过程被意外终止时，用户可直接根据生成的d3dump01文件进行简单重启动分析，不需要对K文件进行任何修改。此时，求解将从意外终止的时刻开始，继续求解至最初预定的求解完成时刻。

（2）小型重启动

当需要对分析的求解设置和模型进行修改，并且仍要继续求解运算时，可采用小型重启动技术。比如，求解达到预定计算时间结束后，发现爆炸仍在继续进行，则用户可以修改计算时长，并将新的K文件和上次求解生成的d3dump01文件递交给求解器进行小型重启动分析。

（3）完全重启动

当需要对数值模型进行较大修改，如需要增减PART、增减接触信息、修改荷载条件和修改控制参数等，则需要用到完全重启动分析。该技术可以在继承前一次分析结果的基础上进行全新的分析。

循环爆破、循环掘进或重复侵彻模拟的具体实现过程可参考本人发布的课程《LS-DYNA岩石循环爆破/重复起爆-完全重启动技术》、《LS-DYNA弹体多次重复侵彻靶体-完全重启动》和《LS-DYNA流固耦合法模拟隧道循环掘进爆破（建炸药、完全重启动）-循环进尺3次》。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删