Fluent粘性模型概述与应用

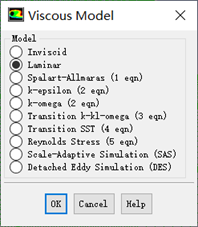
   粘性模型
 

      湍流出现在速度变动的地方。这种波动使得流体介质之间相互交换动量、能量和浓度变化，并且引起了数量的波动。由于这种波动是小尺度且是高频率的，因此在实际工程计算中直接模拟对计算机的要求很高。实际上，瞬时控制方程可能在时间、空间上是均匀的，或者可以人为地改变尺度，这样修改后的方程耗费较少。但是，修改后的方程可能包含我们不知道的变量，湍流模型需要用已知变量确定这些变量。

      Fluent提供的湍流模型包括: Spalart-Allmaras 模型、标准k-ε模型、RNG k-ε模型、带旋流修正k-ε模型、k-ω模型、压力修正k-ω模型、雷诺兹压力模型、大漩涡模拟模型等。

1. Inviscid

进行无粘计算。

2. Laminar

用层流模型进行流动模拟。层流同无粘流动一样，不需要输入任何与计算相关的参数。

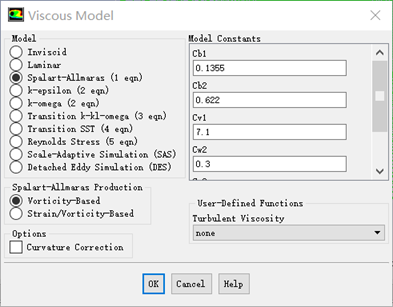
3. Spalart-Allmaras 模型

   S-A模型
 

      Spalart-Allmaras模型是方程模型里面最成功的一个模型，最早被用于有壁面限制情况的流动计算中，特别在存在逆压梯度的流动区域内，对边界层的计算效果较好，因此经常被用于流动分离区附近的计算，后来在涡轮机械的计算中也得到广泛应用。

      最早的Spalart-Allmaras模型用于低雷诺数流计算，特别是在需要准确计算边界层粘性影响的问题中效果较好。Fluent对Spalart-Allmaras 进行了改进，改进后可以在网格精度不高时使用壁面函数。在湍流对流场影响不大，同时网格较粗糙时可以选用这个模型。

注：Spalart-Allmaras模型是一种新出现的湍流模型，在工程应用问题中还没有出现多少成功的算例。如同其他方程模型一样，Spalart-Allmaras模型的稳定性也比较差，在计算中采用Spalart-Allmaras模型时需要注意这个特点。

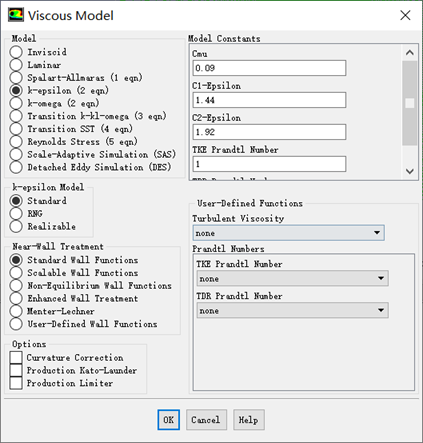
4.标准k-ε模型

   标准k-ε模型
 

      标准k-ε模型由Launder和Spalding提出，模型本身具有的稳定性、经济性和比较高的计算精度使之成为湍流模型中应用范围最广、最为人熟知的一个模型。 标准k-ε模型通过求解湍流动能(k)方程和湍流耗散率(ε) 方程，得到k和ε的解，然后再用k和ε的值计算湍流粘度，最终通过Boussinesq假设得到雷诺应力的解。虽然得到了最广泛的使用，但因为标准k -ε模型假定湍流为各向同性的均匀湍流，所以在旋流(swirl flow)等非均匀湍流问题的计算中存在较大误差，因此后来发展出很多k -ε模型的改进模型，其中包括RNG (重整化群) k -ε模型和Realizable (现实) k -ε模型等衍生模型。

5.RNG k-ε模型

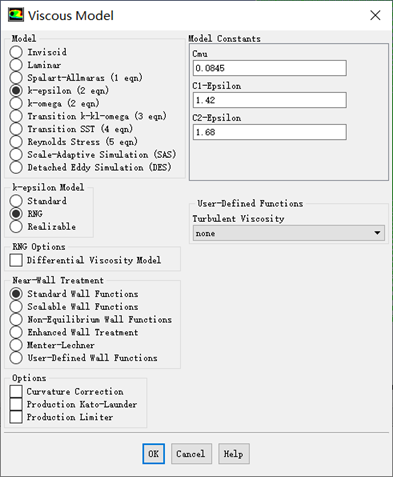
   RNG k-ε模型
 

      RNG k-ε模型在形式上类似于标准k-ε模型，但是在计算功能上要强于标准k-ε模型，改进措施主要有：

(1)在ε方程中增加了一个附加项，使得在计算速度梯度较大的流场时精度更高;

(2)模型中考虑了旋转效应，因此对强旋转流动计算精度也得到提高;

(3)模型中包含了计算湍流Prandtl数的解析公式，而不像标准k-ε模型仅用户定义的常数;

(4)标准k-ε模型是一个高雷诺数模型，而重整化群k-ε模型在对近壁区进行适当的处理后可以计算低雷诺数效应。

6. Realizable k-ε模型

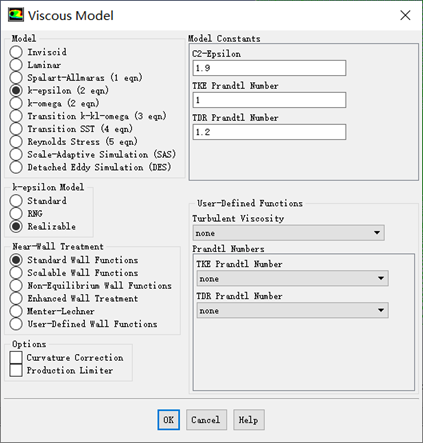
   Realizable k-ε模型
 

      Realizable k -ε模型与标准k-ε模型的主要区别是:

(1)Realizable k -ε模型中采用了新的湍流粘度公式;

(2)ε方程是从涡量扰动量均方根的精确输运方程推导出来的。

      现实k -ε模型满足对雷诺应力的约束条件，因此可以在雷诺应力上保持与真实湍流的一致。这一点是标准k -ε模型和RNG k -ε模型都无法做到的。这个特点在计算中的好处是，可以更精确地模拟平面和圆形射流的打散速度，同时在旋转流计算、带方向压强梯度的边界层计算和分离流计算等问题中，计算结果更符合真实情况。

      Realizable k -ε模型是新出现的k -ε模型。虽然还无法证明其性能已经超过RNG k -ε模型，但是在分离流计算和带二次流的复杂流动计算中的研究表明，Realizable k -ε模型是所有k-ε模型中表现最出色的湍流模型。

      Realizable k-ε模型在同时存在旋转和静止区的流场计算中(如多重参考系、旋转滑移网格等计算中)会产生非物理湍流粘性，因此在类似计算中应该慎重选用这种模型。

7. k-ω模型

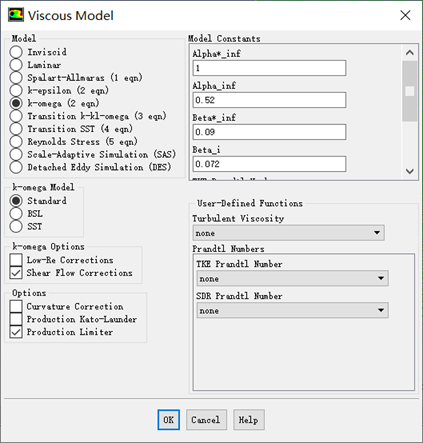
   k-ω模型
 

      k -ω模型也是二方程模型。标准k -ω模型中包含低雷诺数影响、可压缩性影响和剪切流扩散，因此适用于尾迹流动计算、混合层计算、射流计算，以及受到壁面限制的流动计算和自由剪切流计算。

      剪切应力输运k -ω模型简称为SST k-ω模型，综合了k-ω模型在近壁区计算的优点和k-ε模型在远场计算的优点，将k -ω模型和标准k -ε都乘以一个混合函数后再相加就可以得到这个模型。在近壁区,混合函数的值等于1，因此在近壁区等价于k-ω模型。在远离壁面的区域混合函数的值等于0，因此自动转换为标准k-ε模型。

      与标准k-ω模型相比，SST k -ω模型中增加了横向耗散导数项，同时在湍流粘度定义中考虑了湍流剪切应力的输运过程，模型中使用的湍流常数也有所不同。这些特点使得SST k -ω模型的适用范围更广，比如可以用于带逆压梯度的流动计算、翼型计算、跨音速激波计算等。

8.雷诺应力模型(RSM)

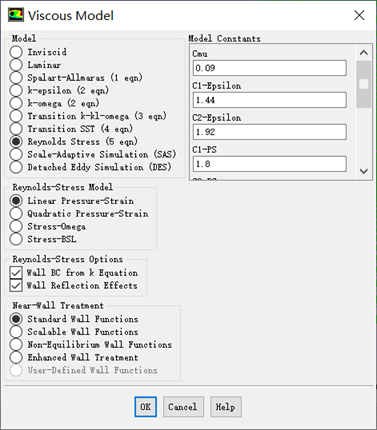
   雷诺应力模型(RSM)

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删