一、 问题描述
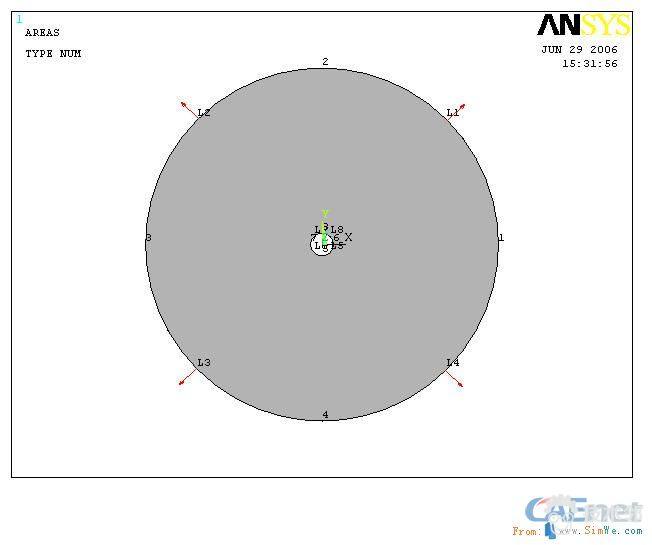
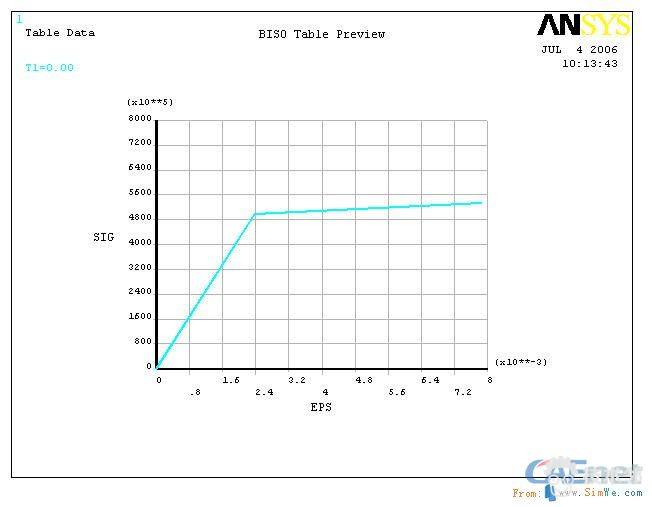
如图所示为一等厚度空心圆盘(参看图1.1),厚度4mm,内径r=10+Δ,Δ=22mm,外径R=500mm,材料属性数据:双线性(参看图1.3)E=2.1×1011Pa,ET=6.0×109Pa,屈服极限σs=500MPa,μ=0.3,密度ρ=8500kg/m3,采用Mises屈服准则,裂纹初始长度为a0=2.0mm。裂纹如图1.2,裂纹位于0度90度180度和270度的位置,图中粗短线表示裂纹。
要求用有限元解
(1) 载荷为均布拉力q=150MPa时的KI。(参看图1.1)
(2) 载荷为均布拉力q=1200MPa时的J积分值。(参看图1.1)
(3) 当载荷为转速n=600r/min的KI ,并计算沿裂纹尖端不同路径的积分值,与KI比较。
二、 求解
求解中统一采用国际单位制,长度m,压力、应力与弹性模量Pa,密度Kg/m3,转速rad/s。
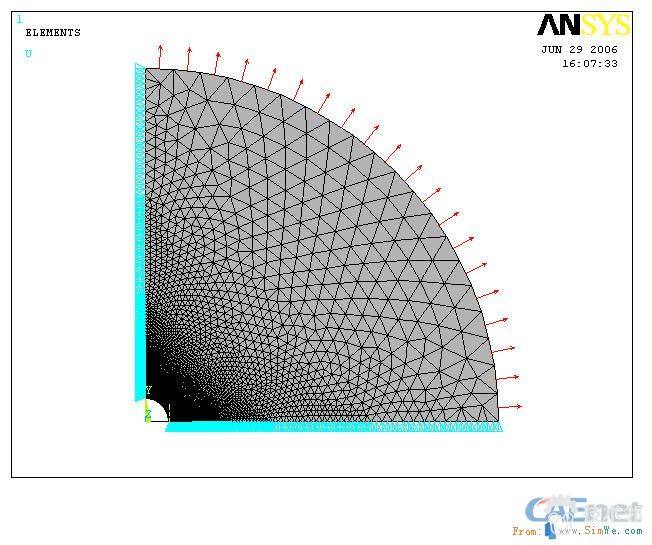
对圆盘的1/4进行 ANSYS建模,网格划分如图2.1。单元类型为6节点三角形单元plane2。裂纹附近单元边长为0.0002m。载荷施加如图2.2,扇形两条半径(裂纹处除外)上施加对称位移边界条件,弧上加均布拉力。裂纹处无位移约束。


计算的应力强度因子和J积分结果如表2.1。前面给出的J积分由于坐标系错误,做法不对,现在改正1200Mpa下的J积分结果。但是,结果差别不大。因为,即使在局部坐标系下,J积分中用到的 XG, YG, ZG的坐标还是在全球坐标系下的。坐标系的改变只对J积分的第一项有一点影响(对Y坐标积分这部分,Y坐标变了)。
新加两个附件:改正后求解1200MPa下J积分的命令流,及两张路径定义的图片命令流里面涉及到路径定义的命令是GUI方式进行的。所以要分开看。
表2.1 应力强度因子和J积分结果
载荷 项目 不同路径下的结果
150MPa KI 3.1359e7 2.986e7 3.3068e7 2.7695e7
(此处J积分没改) J-Integral 3193.41629 3182.07917 3245.22042 3167.23352
1200MPa KI 5.4207e9 5.3398e9 5.382e9 5.285e9
J-Integral 4701408.68 4777189.41 4674756.71 4709657.93
600r/min KI 55011 54901 54672 54463
(此处J积分没改) J-Integral 1.5649802 1.5719383 1.53405748 1.57113766
三、一些需要讨论的问题(后面补的帖解决了大部分问题,这些留在这里供参考):
1、求解方法选择
1200MPa下采用默认的牛顿-拉普生法老是遇到收敛问题,经常不收敛,或者单元高度扭曲。而且需要采用的载荷子步也要很多。(有人做的时候很少遇到这种情况,这与网格划分质量及网格多少有关,网格越少越容易收敛)
采用弧长法能解决这个问题。内径参数r=10+Δ,Δ=22mm 这种情况直接就求出来了。Δ参数不同时可能也不能直接就求出来,也不收敛。但是可以在450,550MPa的地方加两个载荷步就能收敛。如Δ=6mm时,直接用一个载荷步不收敛,我分成150,450,550,1200MPa几个载荷步(依次存为载荷步1,2,3,4)y ,再求解150到1200MPa就成功了(lssolve,1,4,1)。不收敛的原因在于500MPa是屈服极限。
后来验证过,网格画稀一点,不用弧长法直接用默认设置就可以收敛。
2、J积分解法的疑问
我是按照help上的介绍做的,但是对其求解的做法有些怀疑。个人认为求解δuy/δy偏导数的话,应该是把路径沿y方向移动才是对的。Help里面δux/δ x 的求法在数学上正确的。另外,ANSYS里面给了一个路径项求导的操作:general postproc->path operation ->differentiate 。(differentiate是不是求导,请指教) 那这个东西用来求偏导数不行吗? 为什么help 里面要那么来求偏导数。
3、这个实例的建模
这个实例的建模,我是建的1/4模型。1/8模型也可以建出来,但是我对于1/8模型还能不能用对称边界条件有怀疑。1/4模型用对称边界条件是绝对正确的。另外,对称边界条件得到的约束条件在载荷步里面查看到,约束是发生在环向的(柱坐标系下),环向位移约束为零。加约束的时候直接加环向位移为零,也是可以的。
四、 命令流(log文件另附)
1、 建模和求解部分(这里的建模网格划分比较密,可能不是很实用,这里的网格划分不好,在裂纹尖端第一行单元没有奇异性,最好还是用kscon 来做)
2、 J积分部分(对于半边裂纹,如果你已经定义了路径的话,直接把这部分命令流输入进去就可以了)
/post1
!local,11,0,0.034,0,0 !这里不应该建立局部坐标系。只有计算应力强度因子才需要。这里只需要保证全局坐标系的X方向与裂纹平行就是了。
csys,0
!这里应该有一个定义path,这里没有写出。
3、应力强度因子
(1)方法一、先建立局部坐标系:原点在裂纹尖端,x方向与裂纹平行,Y与裂纹垂直,笛卡尔坐标系。定义路径,直接点一下菜单路径就出来了,或者用kcalc就可以了。
(2)方法二、线弹性情况下。先算出J积分然后根据J积分与应力强度因子的关系来求应力强度因子。对于 平面应变模型,J积分=应力强度因子的平方×(1-泊松比×泊松比)/弹性模量
全尺寸裂纹模型前面所建立的模型都只有裂纹的半边。为了验证模型的正确性,后面又建了一个全裂纹的模型。与前面模型的建立方式有一些不同:
1、单元尺寸控制不使用lesize,而是在裂纹尖端用了一个KSCON命令建立concentrate keypoints。单元尺寸很粗糙。
2、模型的建立是在柱坐标系下进行,通过建立直线L实现的笛卡尔坐标下弧线的建立。
3、可能全尺寸裂纹模型的建立方式对大家有参考。主要是裂纹的上下表面在同一个位置,用不同的线/面来表示。
在命令流里面可以看到,直接用程序默认设置求解不收敛。把载荷步设一下就得到了求解结果。结果与前面的模型得到的结果接近。1200Mpa下的应力强度因子为 0.55352E+10,J积分为4657362.7。说明:这个模型中积分路径是完全的。而前面的模型中是半边路径,计算中乘了2。
更新一下全尺寸模型的命令流(文件caenet_060715_002.rar,主要是J积分坐标系的问题)




