产品
继空间后方交会后,继续编程完成空间前方交会,前方交会这不比后方交会简单一万倍?
直接上代码,具体原理及计算方法参考《摄影测量学》(第三版)
Matlab:
clc
clear
close all
tic
%内方位元素
x0 = 0;
y0 = 0;
f = 0.0015291;
%两像片外方位元素(Xs,Ys,Zs,phi,w,kappa)L记录左片,R记录右片
XsYsZsL = [970302.448784,-1138644.971216,3154.584941]';PWKL = [0.010425,-0.012437,0.003380];
XsYsZsR = [971265.303768,-1138634.245942,3154.784258]';PWKR = [0.008870,-0.005062,-0.008703];
%像点坐标l,r
l = [0.00153,0.091798]';
r = [-0.078672,0.089122]';
%分别求左右的旋转矩阵
Rl = getR(PWKL(1),PWKL(2),PWKL(3));
Rr = getR(PWKR(1),PWKR(2),PWKR(3));
%求摄影基线分量(竖着下来是 u,v,w)
B = XsYsZsR - XsYsZsL;
%求像空间辅助坐标
uvwl = Rl*[l;-f];
uvwr = Rr*[r;-f];
%求投影系数公式比较简单,而且只用成对算,所以不用写函数了
N1 = (B(1)*uvwr(3) - B(3)*uvwr(1))/(uvwl(1)*uvwr(3)-uvwr(1)*uvwl(3));
N2 = (B(1)*uvwl(3) - B(3)*uvwl(1))/(uvwl(1)*uvwr(3)-uvwr(1)*uvwl(3));
%计算待定点地面摄影测量坐标
%先求UVW
UVWL = N1*uvwl;
UVWR = N2*uvwr;
%再求XYZ取平均,可以加条件判定是否正确
format longG
XYZL = XsYsZsL+ UVWL
XYZR = XsYsZsR+ UVWR
XYZ_ba = 1/2*(XYZL + XYZR)
toc本次沿用上次的求旋转矩阵的函数:
function [R] = getR(phi,w,kappa)
%此函数传入phi,w,kappa旋转系数,返回旋转矩阵
a1 = cos(phi)* cos(kappa) - sin(phi)* sin(w)* sin(kappa);
a2 = -cos(phi)* sin(kappa) - sin(phi)* sin(w)* cos(kappa);
a3 = -sin(phi)* cos(w);
b1 = cos(w)* sin(kappa);
b2 = cos(w)* cos(kappa);
b3 = -sin(w);
c1 = sin(phi)*cos(kappa) + cos(phi)* sin(w)*sin(kappa);
c2 = -sin(phi)*sin(kappa) + cos(phi)*sin(w)*cos(kappa);
c3 = cos(phi)*cos(w);
R = [a1,a2,a3;
b1,b2,b3;
c1,c2,c3];
endC++代码:
由于要配对左右像片的数据,所以不像后方交会一起平差,本次的类只支持一对一对的点计算
Forward_Intersection.h文件
#pragma once
#include "Eigen/Dense"
//结构体存储左片和右片的点
struct PosePoint;
typedef std::shared_ptr<struct PosePoint> PtrToPP;//定义为智能指针
struct PosePoint
{
double Xs, Ys, Zs,//存储像片的像空间坐标系的原点坐标
phi, w, kappa, //存储φ w κ
x, y; // 像点坐标
};
//前方交会类
class Forward_Intersection
{
public :
Forward_Intersection();
Forward_Intersection(const double &x0 , const double &y0 , const double &f ,PtrToPP pl,PtrToPP pr);//传入两个点的指针的构造函数
//求旋转矩阵,返回旋转矩阵
Eigen::Matrix3d
getR(Eigen::Vector3d &PWK);
//开始计算,返回装有xy的向量
Eigen::Vector3d
startCalculation();
private :
double x0,//内方位元素
y0,
f;
Eigen::Vector3d PWKL;//列向量存储左片φ w κ
Eigen::Vector3d PWKR;//列向量存储右片φ w κ
Eigen::Vector3d XsYsZsL;//列向量存储左片的像空间坐标系的原点坐标
Eigen::Vector3d XsYsZsR;//列向量存储左片的像空间坐标系的原点坐标
Eigen::Vector3d l ;//左片像点坐标
Eigen::Vector3d r ;//右片像点坐标
};Forward_Intersection.cpp文件
#include"Forward_Intersection.h"
Forward_Intersection::Forward_Intersection() {}
Forward_Intersection::Forward_Intersection(const double& x0, const double& y0, const double& f, PtrToPP pl, PtrToPP pr)
:x0(x0),y0(y0),f(f)
{
//把左右点的数据存入对应向量中
this->PWKL << pl->phi,
pl->w,
pl->kappa;
this->PWKR << pr->phi,
pr->w,
pr->kappa;
this->XsYsZsL << pl->Xs,
pl->Ys,
pl->Zs;
this->XsYsZsR << pr->Xs,
pr->Ys,
pr->Zs;
this->l << pl->x ,
pl->y,
-this->f;
this->r << pr->x,
pr->y,
-this->f;
}
//求旋转矩阵
Eigen::Matrix3d
Forward_Intersection::getR(Eigen::Vector3d &PWK)
{
double a1, a2, a3, b1, b2, b3, c1, c2, c3;
Eigen::Matrix3d R;
a1 = cos(PWK(0)) * cos(PWK(2)) - sin(PWK(0)) * sin(PWK(1)) * sin(PWK(2));
a2 = -cos(PWK(0)) * sin(PWK(2)) - sin(PWK(0)) * sin(PWK(1)) * cos(PWK(2));
a3 = -sin(PWK(0)) * cos(PWK(1));
b1 = cos(PWK(1)) * sin(PWK(2));
b2 = cos(PWK(1)) * cos(PWK(2));
b3 = -sin(PWK(1));
c1 = sin(PWK(0)) * cos(PWK(2)) + cos(PWK(0)) * sin(PWK(1)) * sin(PWK(2));
c2 = -sin(PWK(0)) * sin(PWK(2)) + cos(PWK(0)) * sin(PWK(1)) * cos(PWK(2));
c3 = cos(PWK(0)) * cos(PWK(1));
R << a1, a2, a3,
b1, b2, b3,
c1, c2, c3;
return R;
}
Eigen::Vector3d
Forward_Intersection::startCalculation()
{
//旋转矩阵
Eigen::Matrix3d Rl, Rr;
//摄影基线分量(uvw)
Eigen::Vector3d B;
//像空间辅助坐标(左和右)
Eigen::Vector3d uvwl, uvwr;
//投影系数
double N1, N2;
Eigen::Vector3d UVWL, UVWR;
Eigen::Vector3d XYZL, XYZR, XYZ_ba;
//求旋转矩阵
Rl = getR(this->PWKL);
Rr = getR(this->PWKR);
//求摄影基线分量(竖着下来是 u,v,w)
B = this->XsYsZsR - this->XsYsZsL;
//求像空间辅助坐标
uvwl = Rl * l;
uvwr = Rr * r;
//求投影系数
N1 = (B(0) * uvwr(2) - B(2) * uvwr(0)) / (uvwl(0) * uvwr(2) - uvwr(0) * uvwl(2));
N2 = (B(0) * uvwl(2) - B(2) * uvwl(0)) / (uvwl(0) * uvwr(2) - uvwr(0) * uvwl(2));
//先求UVW
UVWL = N1 * uvwl;
UVWR = N2 * uvwr;
//求坐标
XYZL = this->XsYsZsL + UVWL;
XYZR = this->XsYsZsR + UVWR;
XYZ_ba = (XYZL + XYZR);//不能用除号,不知道为啥,好像有什么大病
return XYZ_ba*0.5;
}main函数调试部分:
PtrToPP p1 = make_shared<PosePoint>();
PtrToPP p2 = make_shared<PosePoint>();
p1->Xs = 970302.448784; p1->Ys = -1138644.971216; p1->Zs = 3154.584941;
p2->Xs = 971265.303768; p2->Ys = -1138634.245942; p2->Zs = 3154.784258;
p1->phi = 0.010425; p1->w = -0.012437; p1->kappa = 0.003380;
p2->phi = 0.008870; p2->w = -0.005062; p2->kappa = -0.008703;
p1->x = 0.00153; p1->y = 0.091798;
p2->x = -0.078672; p2->y = 0.089122;
clock_t startTime, endTime;
startTime = clock();//计时开始
Forward_Intersection fi = Forward_Intersection(0, 0, 0.0015291,p1,p2);
Eigen::Vector3d res;
res = fi.startCalculation();
cout << res << endl;
endTime = clock();//计时结束
cout << "运行时间:" << (double)(endTime - startTime) / CLOCKS_PER_SEC << endl;
int temp;
cin >> temp;调试结果:

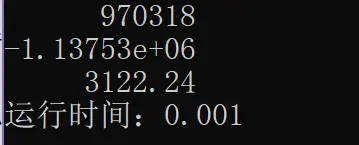
C++终于赢一次。。。