Matlab基础应用笔记：最基础程序应用‌

MATLAB 笔记

①   If   (条件)           或者 多重条件也可以     If  &&  &&  && （多重条件)    

Elesif  （另外条件）

Eles   （其他情况）

End    （结束）

 

②   Input 输入

Fprintf 结果（输出值）   如：（fprintf ( ‘ %g + %g = %g\n ’, a ,b, a+b)  数值加减

 

③      

t=1

while t<=100

disp(hello)        

t=t+2;

end

其中t为计算变量，控制循环次数

 

t=1  

while t<=100     （循环计算1  直到边界而停止）     

    disp(t)

    t=t+2;

end

④   Mod(a  ,b )    求余数 a/b的余数

【④与③结合】

a=input('a=');

b=input('b=');

 

r=mod(a,b);

while r~=0   （~= 意为 不等于； 而== 意为等于 ； =意为取代或代换 ）

     a=b;

 b=r;

 r=mod(a,b);

end

 disp(b)        （disp用于展示数值，而不同于fprintf为输出值）

 

 

⑤  Mod(a  ,b )    求余数 a/b的余数

 

 

⑥  s=0;

for   i= 1:100       （从1每次加1，加至100，也可写成（1：1：100））

    s=s+i;           （也可以逆序加，如 -5：2：10 或 3：-1：5）

   disp (s);

                       （循环计算2  直到边界而停止）

end

 

 

 

⑦   两个函数

1.求拥有几个公倍数   count_factors(n)    结果显示 个数

2.求是否为质数  isprime(n)      结果显示 “1”（拥有）或者 “0”（没有）

 

 

⑧  列举 范围内质数

for i=1:100

         if isprime(i)==1        结果（2  3   5   7 。。。。。。。 97）

        disp(i)

         end

end

 

⑨  图形

X=[-3:0.1:3]

Y=x.*x

Plot=（x,y）              可生成二次函数图

 

且 axis equal             表示将 X轴与y轴的坐标 相等展示

 

Bar(x)             关于x的条形图 ，可包含有正负值

Pie(x)             关于x的饼状图 ，只可包含有正值

 

 

列如 x= 2000:2010;     （共11个单元）

     y=[12 32 334 646 747 78 45 345 246 32 21]        （共11个单元） 

bar(x,y)

 

最终 可生成以x为底轴 y为高轴的 条形图

 

⑩   三位图像

 Theta=0:pi/100:12pi;

X=cos(theta);

Y=sin(theta);

Z=0:1200

Plot3=( x , y, z )               ( 关键，三维图像生成函数公式 )

 

 

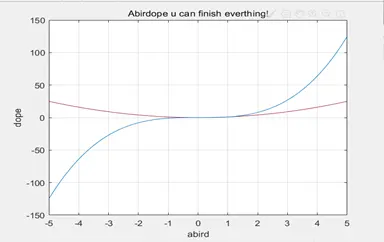
⑪  图像标注

x1=-5:0.1:5;    

y1=x1.*x1;                    (生成二次元图像)

plot(x1,y1);

 

hold on ;                        （对比，或是同是 存在多个图像）

 

x2=-5:0.1:5;

y2=x2.*x2.*x2;                 (生成三次元图像)

plot(x2,y2);

 

grid on;                        （生成 网络格纹）

title('Abirdope u can finish everthing!');    （图像总标题 设置）

xlabel('abird');                        （图像 x轴设置标题）

ylabel('dope');                        （图像 y轴设置标题）

z label(' black ');                       （用于三维）

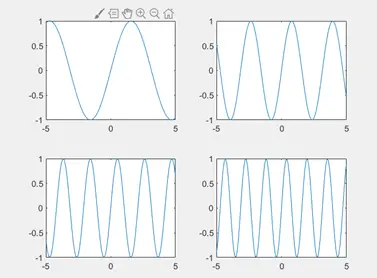
⑫  多区位图像

x=-5:0.1:5;

y1=sin(x);        y3=sin(3.*x);

y2=sin(2.*x);      y4=sin(4.*x);

 

subplot(2,2,1);       （意为布局为2X2的区位，且此时生成的为第一顺位的图像）

plot(x,y1);           【 特殊区位，将3、4区块合并 → subplot( 2 , 2 , [ 3 , 4 ] ) 】

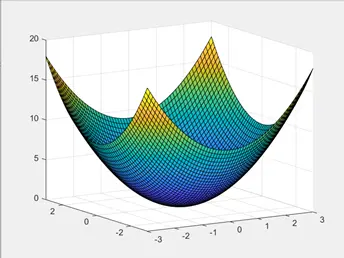
⑬  三维曲面

x=-3:0.1:3;     （x轴的坐标点）

y=-3:0.1:3;     （y轴的坐标点）

[X,Y]=meshgrid(x,y);   (将x与y坐标组合 成体一平面，且生成X、Y)   [生成矩阵]

Z=X.^2+Y.^2;      （X与Y关于Z的函数）

surf(X,Y,Z)          （’’surf’’用于生成 三维去曲面的函数公式）

 

 ⑭  Legend     (生成函数曲线对照表，即注释)

x1=-3:0.1:3;

y1=-3:0.1:3;

y2=x1.*x1;

y3=sin(x1);

y4=cos(x1);

 

plot(x1,y3,'xc',x1,y4,'xb',x1,y2,'or');

legend( 'x1.*x1' , 'sin(x1)' , 'cos(x1)' );

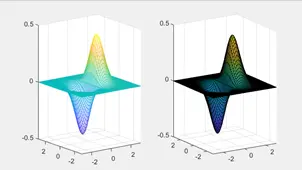
 ⑮  Surf与 mesh的区别

Mesh 用于绘制不是特别精细的三维曲面网格图，同一层面的线条用相同的颜色表示，即使线条补面之间无颜色。

   Surf  用于绘制比较光滑的三维曲面网格图，各线条之间的补面用颜色填充，即使线条补面之间有颜色。

⑯  RelTol',与 ,'AbsTo的区别

options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]); 是解微分方程时的选项设置，'RelTol',1e-4,是相对误差设置，'AbsTol',[1e-4 1e-4 1e-5]是绝对误差设置

链接：

https://zhidao.baidu.com/question/1883144514365821148.html?qbl=relate_question_1&word=matlab%D6%D0odeset

 持续更新 R-K ， Matlab ，SOLIDWORKS 等知识  

欢迎 同学们一起交流学习 共同进步  

总所周知 ，哔哩哔哩 是一个学习网站（手动 狗头） 

看到这里 留着  赞  呗~   嘻嘻嘻