在逆向过程中经常要求解一些数学问题,譬如矩阵、极限、微积分、多元二次方程、因式分解等,如果掌握如下工具可以迎刃而解。
1、z3
Z3 是一个微软出品的开源约束求解器,能够解决很多种情况下的给定部分约束条件寻求一组满足条件的解的问题,可以简单理解为解方程的感觉,功能强大且易于使用。这个库可以解决所有的方程,如果有解。
编译Z3非常费时间,大概几十分钟,在Kali Linux下安装成功。Z3 v4.3.0不支持python 3.3。我们必须使用 python 2.7 ( 或者 2.6 ) 。
安装步骤:
tar –zxvf z3-solver-4.8.0.0.post1.tar.gz
root@kali:~/z3-solver-4.8.0.0.post1#python setup.py build
root@kali:~/z3-solver-4.8.0.0.post1#python setup.py install
例子:测试如下代码
>>>from z3 import *
>>>x, y ,z = BitVecs('x y z', 64)
>>>solve(((x - y) << 2) + x + z == 0xEAF917E2,((x - y) << 1) +
(x - y) + x + z == 0xE8F508C8,((x - y) << 1) + (x - y) + x - z == 0x0C0A3C68)
[z = 1853187632, y = 1919903280, x = 1953723722]
2、numpy
numpy可以安装为python的一个模块,主要解决矩阵问题。
例子:
import numpy as np
a = np.array([
[30971, 31063, 18211, 23911, 20327, 20921, 20149,17477],
[20051, 20359, 16699, 31121, 20641, 23633, 29759,25111],
[25943, 27073, 25561, 23333, 26099, 17291,27457, 30839],
[29873, 18313, 29167, 25411, 32191, 18959,19079, 16879],
[16607, 29437, 19469, 32441, 28859, 20509, 23581, 26849],
[16823, 19927, 26161, 18869, 19973, 26981,17431, 26633],
[26821, 19073, 28349, 30577, 25793, 22091,31397, 26947],
[25339, 17737, 30817, 26183, 29629, 22691,27793, 19447]
])
b = np.array([14985352,14962906, 16361024, 14982624, 16152948, 14720714, 16722910, 15883204])
r =np.linalg.solve(a,b)
print r
3、Wolfram Mathematica
可以到网站https://www.wolframalpha.com/在线求解
例:因式分解-a^4-b^4-c^4+2*a^2*b^2+2*b^2*c^2+2*a^2*c^2
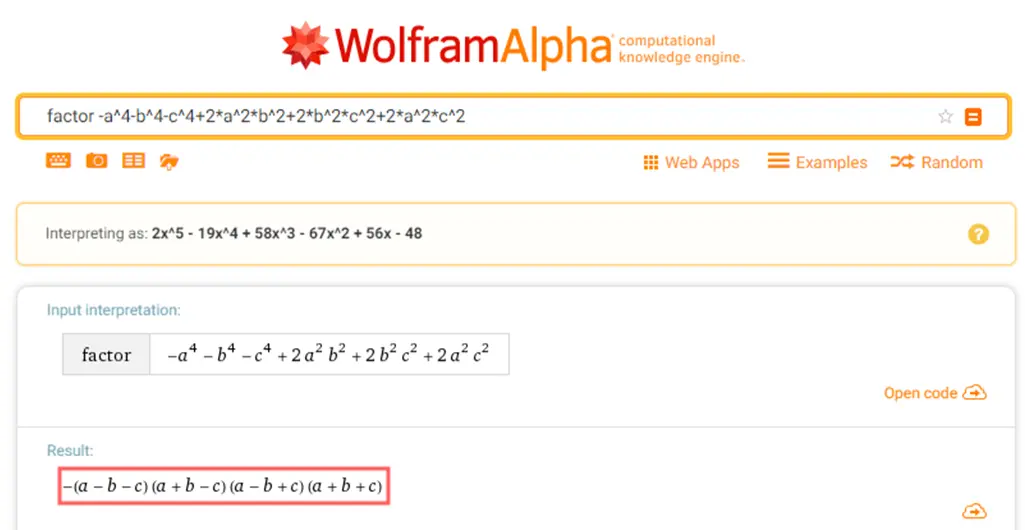
也可以在电脑中安装Wolfram Mathematica进行计算

4、sage
Sage(或称SageMath)是在GPL协议下发布的开源数学软件,并且整合了许多已有的开源软件包到一个基于Python的统一界面下。其目标是创造一个Magma,Maple,Mathematica和Matlab的开源替代品。
Sage包含了从线性代数、微积分,到密码学、数值计算、组合数学、群论、图论、数论等各种初高等数学的计算功能。
例:
x=var(x)
f(x)=(pow(x,2)-3*x+2)/(pow(x,2)-4)
r1=4*lim(f(x),x=2)
print(r1)
5、sympy库
SymPy一个用于符号型数学计算(symbolic mathematics)的Python库。它旨在成为一个功能齐全的计算机代数系统(Computer Algebra System,CAS),同时保持代码简洁、易于理解和扩展。SymPy完全是用Python写的,并不需要外部的库。
可以求解下述问题:求解线性方程组、求解微积分问题、求解极限问题、矩阵化简等。
>>> from sympy import *
>>> x=Symbol('x')
>>> y=Symbol('y')
>>> z=Symbol('z')
>>> print (solve([4*(x - y) + x + z-0xEAF917E2,2*(x - y) + (x - y) + x + z-0xE8F508C8, 2*(x - y) + (x - y) + x - z-0x0C0A3C68],[x,y,z]))
{x: 1953723722, z: 1853187632, y: 1919903280}




