智能控制仿真实例代码精选与解析

刘金琨智能控制（第2版）仿真实例代码整理_自适应

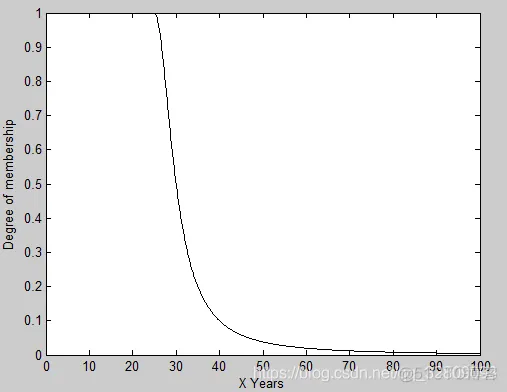
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_02

图3-1 “年轻”的隶属函数曲线

“年轻”的隶属函数仿真程序：chap3_1.m

%Membership function for Young People “年轻”的隶属函数曲线
clear all;
close all;

for k=1:1:1001
x(k)=(k-1)*0.10;% x取值范围0~100
if x(k)>=0&x(k)<=25
y(k)=1.0;
else
y(k)=1/(1+((x(k)-25)/5)^2);
end
end
plot(x,y,'k');
xlabel('X Years');ylabel('Degree of membership');

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_03 刘金琨智能控制（第2版）仿真实例代码整理_自适应_04

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_05 刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_06

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_07 刘金琨智能控制（第2版）仿真实例代码整理_自适应_08
刘金琨智能控制（第2版）仿真实例代码整理_自适应_09

典型隶属函数仿真程序：chap3_2.m

%Membership function
clear all;
close all;

M=1;
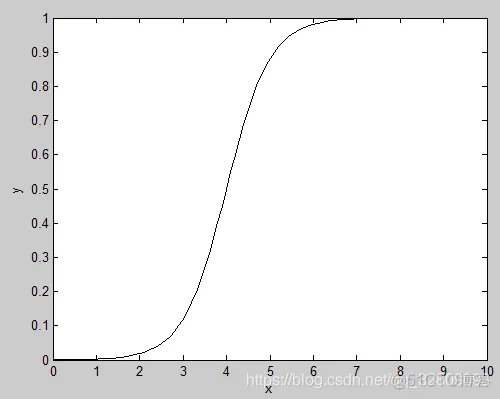
if M==1 %Guassian membership function 高斯型隶属函数
x=0:0.1:10;
y=gaussmf(x,[5 2]); %高斯函数依赖两个参数，gaussmf(x,[sig,c])
plot(x,y,'k');
xlabel('x');ylabel('y');

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_10
elseif M==2 %General Bell membership function 广义钟型隶属函数
x=0:0.1:10;
y=gbellmf(x,[2 4 6]);
plot(x,y,'k');
xlabel('x');ylabel('y');

刘金琨智能控制（第2版）仿真实例代码整理_自适应_11
elseif M==3 %S membership function S型隶属函数
x=0:0.1:10;
y=sigmf(x,[2 4]);
plot(x,y,'k');
xlabel('x');ylabel('y');

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_12
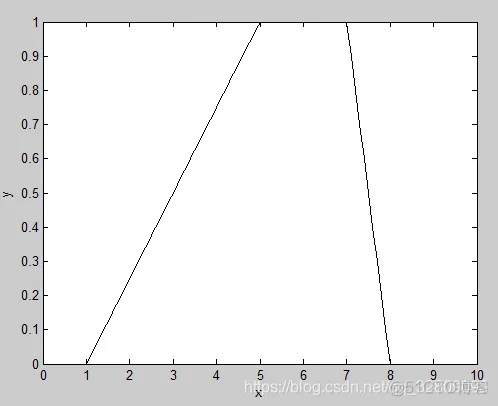
elseif M==4 %Trapezoid membership function 梯形隶属函数
x=0:0.1:10;
y=trapmf(x,[1 5 7 8]);
plot(x,y,'k');
xlabel('x');ylabel('y');

刘金琨智能控制（第2版）仿真实例代码整理_自适应_13
elseif M==5 %Triangle membership function 三角型隶属函数
x=0:0.1:10;
y=trimf(x,[3 6 8]);
plot(x,y,'k');
xlabel('x');ylabel('y');

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_14
elseif M==6 %Z membership function Z型隶属函数
x=0:0.1:10;
y=zmf(x,[3 7]);
plot(x,y,'k');
xlabel('x');ylabel('y');
end

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_15

设计一个三角形隶属函数，按[-3，3]范围七个等级，建立一个模糊系统，用来表示{负大，负中，负小，零，正小，正中，正大}。

模糊系统隶属函数设计程序：chap3_3.m

%Define N+1 triangle membership function 定义N+1个模糊等级
clear all;
close all;
N=6;

x=-3:0.01:3; %定义x范围为-3~3
for i=1:N+1
f(i)=-3+6/N*(i-1);
end
u=trimf(x,[f(1),f(1),f(2)]); % [-3 -3 -2]三角函数负大
figure(1);
plot(x,u);
for j=2:N
u=trimf(x,[f(j-1),f(j),f(j+1)]); % [-3 -2 -1]~[1 2 3]三角函数负中、负小、零、正小、正中
hold on;
plot(x,u);
end
u=trimf(x,[f(N),f(N+1),f(N+1)]);%[2 3 3]三角函数正大
hold on;
plot(x,u);
xlabel('x');
ylabel('Degree of membership');

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_16

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_17

模糊矩阵合成：chap3_4.m

clear all;
close all;
A=[0.8,0.7;
0.5,0.3];
B=[0.2,0.4;
0.6,0.9];
%Compound of A and B
for i=1:2
for j=1:2
AB(i,j)=max(min(A(i,:),B(:,j)'))% AB(i,j)等于A的第i行与B的第j列取小后取大
end
end
%Compound of B and A
for i=1:2
for j=1:2
BA(i,j)=max(min(B(i,:),A(:,j)'))
end
end

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_18 刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_19

第4章模糊控制

以水位的模糊控制为例，如图4-4所示。设有一个水箱，通过调节阀可向内注水和向外抽水。设计一个模糊控制器，通过调节阀门将水位稳定在固定点附近。按照日常的操作经验，可以得到基本的控制规则：

“若水位高于O点，则向外排水，差值越大，排水越快”；

“若水位低于O点，则向内注水，差值越大，注水越快”。

根据上述经验，按下列步骤设计模糊控制器：

刘金琨智能控制（第2版）仿真实例代码整理_自适应_20

1 确定观测量和控制量

定义理想液位O点的水位为h0，实际测得的水位高度为h，选择液位差e，将当前水位对于O点的偏差e作为观测量。

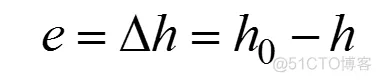
刘金琨智能控制（第2版）仿真实例代码整理_智能控制_21

2 输入量和输出量的模糊化

将偏差e分为五个模糊集：负大（NB），负小（NS），零（O），正小（PS），正大（PB）。根据偏差e的变化范围分为七个等级：-3，-2，-1，0，+1，+2，+3。得到水位变化模糊表4-1。

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_22

控制量u为调节阀门开度的变化。将其分为五个模糊集：负大（NB），负小（NS），零（O），正小（PS），正大（PB）。并根据u的变化范围分为九个等级：-4，-3，-2，-1，0，+1，+2，+3，+4。得到控制量模糊划分表4-2。

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_23

3 模糊规则的描述

根据日常的经验，设计以下模糊规则：

（1）“若e负大，则u负大”

（2）“若e负小，则u负小”

（3）“若e为0，则u为0”

（4）“若e正小，则u正小”

（5）“若e正大，则u正大”

其中，排水时，u为负，注水时，u为正。

上述规则采用“IF A THEN B”形式来描述：

（1） if e=NB then u=NB

（2） if e=NS then u=NS

（3） if e=0 then u=0

（4） if e=PS then u=PS

（5） if e=PB then u=PB

根据上述经验规则，可得模糊控制表4-3。

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_24

4 求模糊关系

模糊控制规则是一个多条语句，它可以表示为U×V上的模糊子集，即模糊关系R：

刘金琨智能控制（第2版）仿真实例代码整理_自适应_25

5 模糊决策

模糊控制器的输出为误差向量和模糊关系的合成：

刘金琨智能控制（第2版）仿真实例代码整理_自适应_26

6 控制量的反模糊化

由模糊决策可知，当误差为负大时，实际液位远高于理想液位，e=NB，控制器的输出为一模糊向量，可表示为：

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_27

如果按照“隶属度最大原则”进行反模糊化，则选择控制量为u=-4，即阀门的开度应关大一些，减少进水量。

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_28

水箱液位模糊控制仿真程序：chap4_1.m

%Fuzzy Control for water tank
clear all;
close all;

a=newfis('fuzz_tank');%创建一个FIS对象a

a=addvar(a,'input','e',[-3,3]); %Parameter e 误差e隶属度函数
a=addmf(a,'input',1,'NB','zmf',[-3,-1]);% Z型隶属函数
a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);%三角隶属函数
a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);
a=addmf(a,'input',1,'PB','smf',[1,3]);% S型隶属函数

a=addvar(a,'output','u',[-4,4]); %Parameter u 控制量u隶属度函数
a=addmf(a,'output',1,'NB','zmf',[-4,-1]);
a=addmf(a,'output',1,'NS','trimf',[-4,-2,1]);
a=addmf(a,'output',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'output',1,'PS','trimf',[-1,2,4]);
a=addmf(a,'output',1,'PB','smf',[1,4]);

rulelist=[1 1 1 1; %Edit rule base
2 2 1 1;
3 3 1 1;
4 4 1 1;
5 5 1 1];

a=addrule(a,rulelist);%增加模糊推理规则，a为模糊规则库

a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy 解模糊化采用的是最大隶属度平均法（选取结果中隶属度最大的元素作为输出值）
writefis(a1,'tank'); %Save to fuzzy file "tank.fis" 保存到模糊文件tank.fis
a2=readfis('tank');

figure(1);
plotfis(a2);%模糊控制系统a2

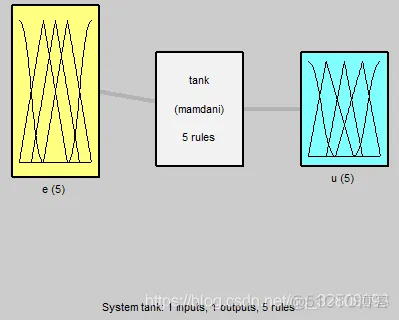
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_29
figure(2);
plotmf(a,'input',1);%输入模糊集

刘金琨智能控制（第2版）仿真实例代码整理_自适应_30
figure(3);
plotmf(a,'output',1);%输出模糊集

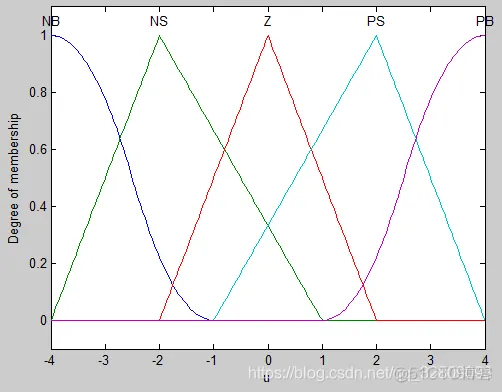
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_31

flag=1;
if flag==1
showrule(a) %Show fuzzy rule base 显示模糊控制规则

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_32
ruleview('tank'); %Dynamic Simulation 动态仿真tank

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_33
end
disp('-------------------------------------------------------');
disp(' fuzzy controller table:e=[-3,+3],u=[-4,+4] ');
disp('-------------------------------------------------------');

for i=1:1:7
e(i)=i-4;
Ulist(i)=evalfis([e(i)],a2);%输入为e,利用a2进行模糊推理，结果给Ulist(i),得出控制响应u

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_34
end
Ulist=round(Ulist)

e=-3; % Error
u=evalfis([e],a2) %Using fuzzy inference 利用a2对e=-3进行模糊推理

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_35

输入e改为2时：

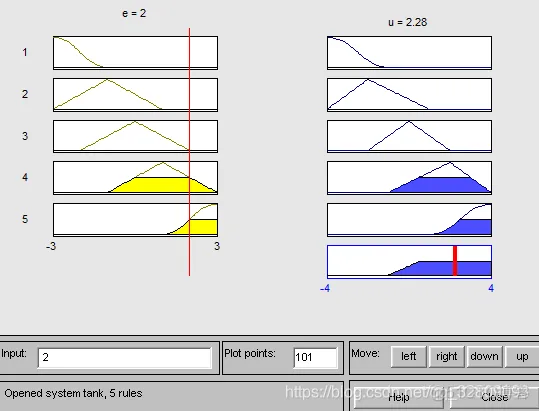
刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_36

输入e改为-2.5时：

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_37

建立二输入单输出模糊控制系统，该系统包括两个部分，即模糊控制器的设计和位置跟踪。控制规则为49条。误差、误差变化率为[-3,3], 控制输入的范围均为[-4.5,4.5]。模糊规则表如表4-5所示:

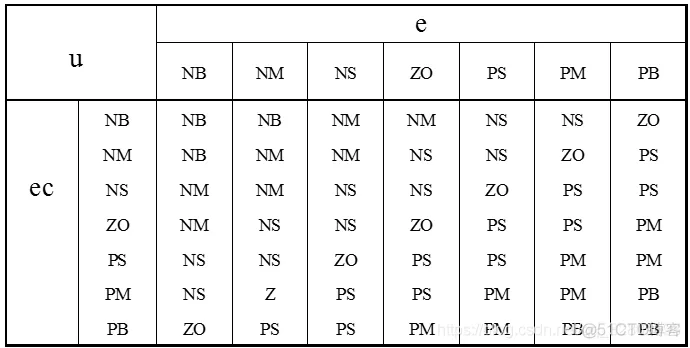
刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_38

模糊控制器的设计仿真：chap4_2.m

%Fuzzy Controller Design
clear all;
close all;

a=newfis('fuzzf');%创建一个FIS对象a

f1=0.1;
a=addvar(a,'input','e',[-3*f1,3*f1]); %Parameter e 误差e隶属度函数，在a中添加变量
a=addmf(a,'input',1,'NB','zmf',[-3*f1,-1*f1]);
a=addmf(a,'input',1,'NM','trimf',[-3*f1,-2*f1,0]);
a=addmf(a,'input',1,'NS','trimf',[-3*f1,-1*f1,1*f1]);
a=addmf(a,'input',1,'Z','trimf',[-2*f1,0,2*f1]);
a=addmf(a,'input',1,'PS','trimf',[-1*f1,1*f1,3*f1]);
a=addmf(a,'input',1,'PM','trimf',[0,2*f1,3*f1]);
a=addmf(a,'input',1,'PB','smf',[1*f1,3*f1]);

f2=0.1;
a=addvar(a,'input','ec',[-3*f2,3*f2]); %Parameter ec 误差变化率隶属度函数
a=addmf(a,'input',2,'NB','zmf',[-3*f2,-1*f2]);
a=addmf(a,'input',2,'NM','trimf',[-3*f2,-2*f2,0]);
a=addmf(a,'input',2,'NS','trimf',[-3*f2,-1*f2,1*f2]);
a=addmf(a,'input',2,'Z','trimf',[-2*f2,0,2*f2]);
a=addmf(a,'input',2,'PS','trimf',[-1*f2,1*f2,3*f2]);
a=addmf(a,'input',2,'PM','trimf',[0,2*f2,3*f2]);
a=addmf(a,'input',2,'PB','smf',[1*f2,3*f2]);

f3=10;
a=addvar(a,'output','u',[-3*f3,3*f3]); %Parameter u 控制量u隶属度函数
a=addmf(a,'output',1,'NB','zmf',[-3*f3,-1*f3]);
a=addmf(a,'output',1,'NM','trimf',[-3*f3,-2*f3,0]);
a=addmf(a,'output',1,'NS','trimf',[-3*f3,-1*f3,1*f3]);
a=addmf(a,'output',1,'Z','trimf',[-2*f3,0,2*f3]);
a=addmf(a,'output',1,'PS','trimf',[-1*f3,1*f3,3*f3]);
a=addmf(a,'output',1,'PM','trimf',[0,2*f3,3*f3]);
a=addmf(a,'output',1,'PB','smf',[1*f3,3*f3]);

rulelist=[1 1 1 1 1; %Edit rule base 49条规则
1 2 1 1 1;
1 3 2 1 1;
1 4 2 1 1;
1 5 3 1 1;
1 6 3 1 1;
1 7 4 1 1;

2 1 1 1 1;
2 2 2 1 1;
2 3 2 1 1;
2 4 3 1 1;
2 5 3 1 1;
2 6 4 1 1;
2 7 5 1 1;

3 1 2 1 1;
3 2 2 1 1;
3 3 3 1 1;
3 4 3 1 1;
3 5 4 1 1;
3 6 5 1 1;
3 7 5 1 1;

4 1 2 1 1;
4 2 3 1 1;
4 3 3 1 1;
4 4 4 1 1;
4 5 5 1 1;
4 6 5 1 1;
4 7 6 1 1;

5 1 3 1 1;
5 2 3 1 1;
5 3 4 1 1;
5 4 5 1 1;
5 5 5 1 1;
5 6 6 1 1;
5 7 6 1 1;

6 1 3 1 1;
6 2 4 1 1;
6 3 5 1 1;
6 4 5 1 1;
6 5 6 1 1;
6 6 6 1 1;
6 7 7 1 1;

7 1 4 1 1;
7 2 5 1 1;
7 3 5 1 1;
7 4 6 1 1;
7 5 6 1 1;
7 6 7 1 1;
7 7 7 1 1];

a=addrule(a,rulelist);%在a中增加模糊推理规则，a为模糊规则库
%showrule(a) % Show fuzzy rule base 显示FIS对象a的规则

a1=setfis(a,'DefuzzMethod','mom');%Defuzzy 解模糊化采用的是最大隶属度平均法（选取结果中隶属度最大的元素作为输出值）
writefis(a1,'fuzzf'); % save to fuzzy file "fuzz.fis" which can be 保存到模糊文件tank.fis
% simulated with fuzzy tool
a2=readfis('fuzzf');%从磁盘装入FIS
disp('-------------------------------------------------------');
disp(' fuzzy controller table:e=[-3,+3],ec=[-3,+3] ');
disp('-------------------------------------------------------');

Ulist=zeros(7,7);

for i=1:7
for j=1:7
e(i)=-4+i;
ec(j)=-4+j;
Ulist(i,j)=evalfis([e(i),ec(j)],a2);%输入为e、ec,利用a2进行模糊推理，结果给Ulist(i,j),得出控制响应u（完成模糊推理计算）

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_39
end
end

Ulist=ceil(Ulist)

figure(1);
plotfis(a2);%绘制模糊推理系统FIS对象a2

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_40
figure(2);
plotmf(a,'input',1);%输入模糊集e（偏差隶属度函数）plotmf--绘制给定变量的隶属度函数

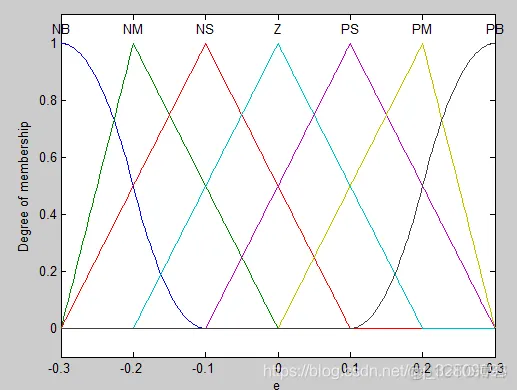
刘金琨智能控制（第2版）仿真实例代码整理_智能控制_41
figure(3);
plotmf(a,'input',2);%输入模糊集ec（偏差变化率隶属度函数）

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_42
figure(4);
plotmf(a,'output',1);%输出模糊集u（控制器输出隶属度函数）

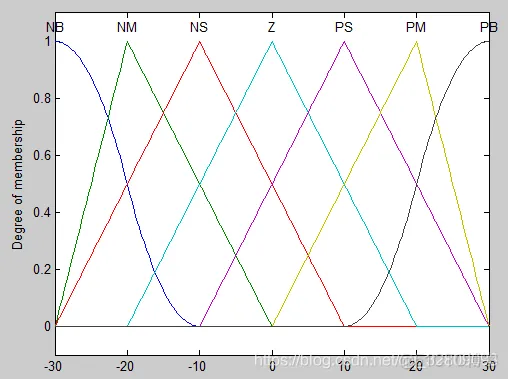
刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_43

模糊控制位置跟踪:被控对象为

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_44

首先运行模糊控制器程序chap4_2.m，并将模糊控制系统保存在a2之中。然后运行模糊控制的Simulink仿真程序chap4_3.mdl，位置指令取正弦信号0.5sin(10t)

注：当前目录要设置为同一文件夹（chap4_2.m与chap4_3.mdl） 1HZ=2*pi rad/sec

刘金琨智能控制（第2版）仿真实例代码整理_自适应_45

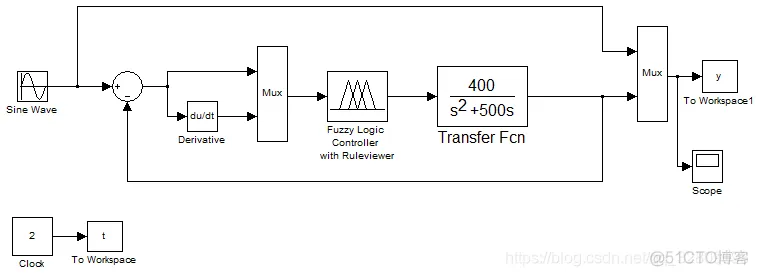
刘金琨智能控制（第2版）仿真实例代码整理_自适应_46

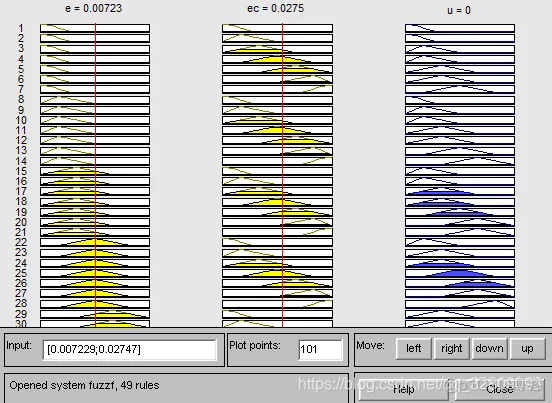
刘金琨智能控制（第2版）仿真实例代码整理_智能控制_47

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_48

改变输入信号为1sin(5t)

刘金琨智能控制（第2版）仿真实例代码整理_自适应_49

模糊洗衣机的设计:

选用单变量二维模糊控制器。控制器的输入为衣物的污泥和油脂，输出为洗涤时间。

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_50

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_51

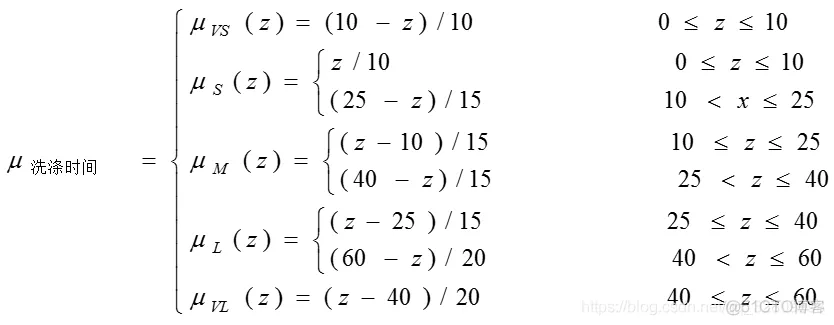
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_52

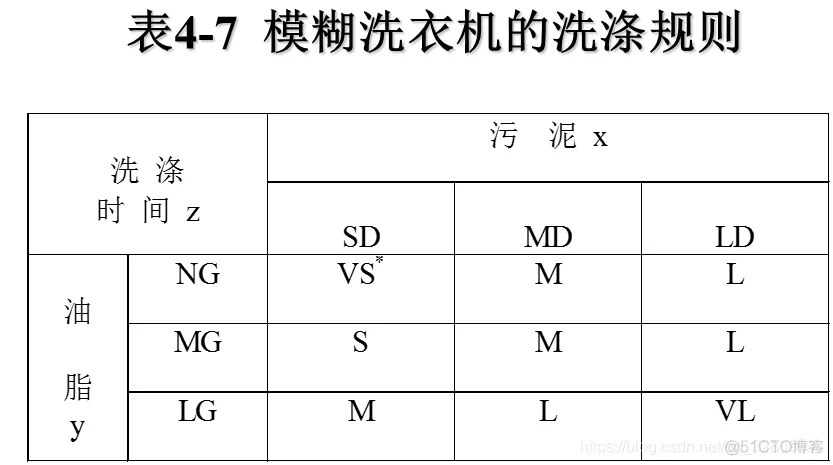
刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_53

采用MATLAB中模糊控制工具箱中的模糊命令设计洗衣机模糊控制系统，采用本节的隶属函数，按上述步骤设计模糊系统。取x=60，y=70，反模糊化采用最大隶属平均法，模糊推理结果为24.9。利用命令showrule可观察规则库，利用命令ruleview可实现模糊控制的动态仿真。

洗衣机模糊控制系统程序：chap4_6.m

%Fuzzy Control for washer
clear all;
close all;

a=newfis('fuzz_wash');%创建一个FIS对象a

a=addvar(a,'input','x',[0,100]); %Fuzzy Stain 模糊集合
a=addmf(a,'input',1,'SD','trimf',[0,0,50]); %污泥隶属函数
a=addmf(a,'input',1,'MD','trimf',[0,50,100]);
a=addmf(a,'input',1,'LD','trimf',[50,100,100]);

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_54

a=addvar(a,'input','y',[0,100]); %Fuzzy Axunge 油脂隶属函数
a=addmf(a,'input',2,'NG','trimf',[0,0,50]);
a=addmf(a,'input',2,'MG','trimf',[0,50,100]);
a=addmf(a,'input',2,'LG','trimf',[50,100,100]);

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_55

a=addvar(a,'output','z',[0,60]); %Fuzzy Time 洗涤时间隶属函数
a=addmf(a,'output',1,'VS','trimf',[0,0,10]);
a=addmf(a,'output',1,'S','trimf',[0,10,25]);
a=addmf(a,'output',1,'M','trimf',[10,25,40]);
a=addmf(a,'output',1,'L','trimf',[25,40,60]);
a=addmf(a,'output',1,'VL','trimf',[40,60,60]);

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_56

rulelist=[1 1 1 1 1; %Edit rule base 9条规则
1 2 3 1 1;
1 3 4 1 1;

2 1 2 1 1;
2 2 3 1 1;
2 3 4 1 1;

3 1 3 1 1;
3 2 4 1 1;
3 3 5 1 1];

a=addrule(a,rulelist); %在a中增加模糊推理规则，a为模糊规则库

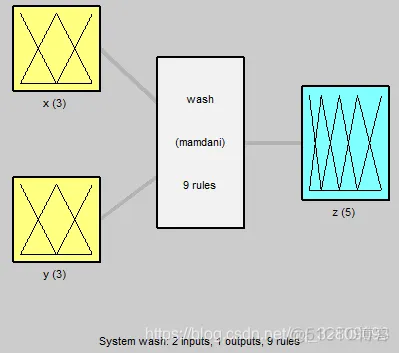
刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_57
showrule(a) %Show fuzzy rule base 显示规则库

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_58

a1=setfis(a,'DefuzzMethod','mom'); %Defuzzy 最大隶属平均法解模糊化
writefis(a1,'wash'); %Save to fuzzy file "wash.fis" 保存到模糊文件wash.fis
a2=readfis('wash'); %从磁盘装入FIS

figure(1);
plotfis(a2); %绘制模糊推理系统FIS对象a2
figure(2);
plotmf(a,'input',1); %输出污泥隶属函数
figure(3);
plotmf(a,'input',2); %输出油脂隶属函数
figure(4);
plotmf(a,'output',1); %输出洗涤时间隶属函数

ruleview('wash'); %Dynamic Simulation 模糊控制的动态仿真

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_59

%取污泥为60，油脂为70时，推理洗涤时间z
x=60;
y=70;
z=evalfis([x,y],a2) %Using fuzzy inference 使用模糊推理

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_60

4.5 模糊自适应整定PID控制

自适应模糊PID控制器以误差e和误差变化ec作为输入，可以满足不同时刻的e和ec对PID参数自整定的要求。利用模糊控制规则在线对PID参数进行修改，便构成了自适应模糊PID控制器

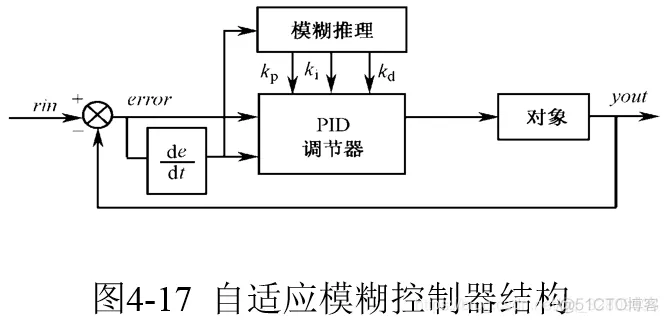
刘金琨智能控制（第2版）仿真实例代码整理_智能控制_61

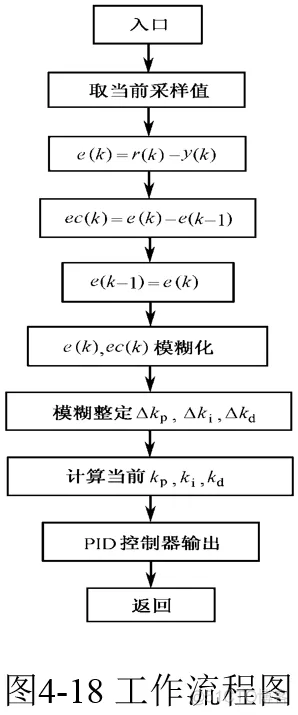
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_62

4.5.2 仿真实例

被控对象为刘金琨智能控制（第2版）仿真实例代码整理_智能控制_63

采样时间为1ms，采用z变换进行离散化，离散化后的被控对象为：

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_64

位置指令为幅值为1.0的方波信号。仿真时，先运行模糊推理系统设计程序chap4_7a.m，实现模糊推理系统fuzzpid.fis的设计，并将此模糊推理系统调入内存中，然后运行模糊控制程序chap4_7b.m。

模糊PID系统程序：chap4_7a.m

%Fuzzy Tunning PID Control
clear all;
close all;

a=newfis('fuzzpid');%创建一个FIS对象a

a=addvar(a,'input','e',[-3,3]); %Parameter e 误差e隶属度函数，在a中添加变量
a=addmf(a,'input',1,'NB','zmf',[-3,-1]);
a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);
a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);
a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);
a=addmf(a,'input',1,'PM','trimf',[0,2,3]);
a=addmf(a,'input',1,'PB','smf',[1,3]);

刘金琨智能控制（第2版）仿真实例代码整理_自适应_65

a=addvar(a,'input','ec',[-3,3]); %Parameter ec 误差变化率隶属度函数
a=addmf(a,'input',2,'NB','zmf',[-3,-1]);
a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);
a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);
a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);
a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);
a=addmf(a,'input',2,'PM','trimf',[0,2,3]);
a=addmf(a,'input',2,'PB','smf',[1,3]);

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_66

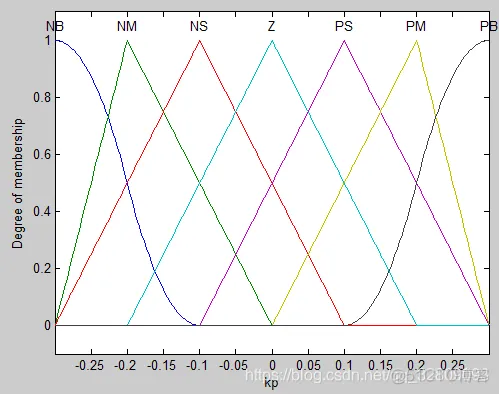
a=addvar(a,'output','kp',[-0.3,0.3]); %Parameter kp 比例系数kp隶属度函数
a=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);
a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);
a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);
a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);
a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);
a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);
a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_67

a=addvar(a,'output','ki',[-0.06,0.06]); %Parameter ki 积分作用系数ki隶属度函数
a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);
a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);
a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]);
a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);
a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);
a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);
a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_68

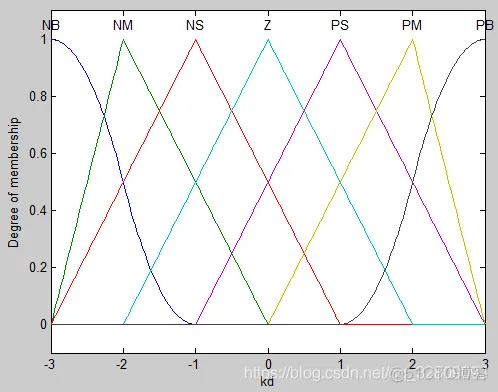
a=addvar(a,'output','kd',[-3,3]); %Parameter kd 微分作用系数kd隶属度函数
a=addmf(a,'output',3,'NB','zmf',[-3,-1]);
a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);
a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);
a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);
a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);
a=addmf(a,'output',3,'PM','trimf',[0,2,3]);
a=addmf(a,'output',3,'PB','smf',[1,3]);

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_69

rulelist=[1 1 7 1 5 1 1; %Edit rule base 49条规则
1 2 7 1 3 1 1;
1 3 6 2 1 1 1;
1 4 6 2 1 1 1;
1 5 5 3 1 1 1;
1 6 4 4 2 1 1;
1 7 4 4 5 1 1;

2 1 7 1 5 1 1;
2 2 7 1 3 1 1;
2 3 6 2 1 1 1;
2 4 5 3 2 1 1;
2 5 5 3 2 1 1;
2 6 4 4 3 1 1;
2 7 3 4 4 1 1;

3 1 6 1 4 1 1;
3 2 6 2 3 1 1;
3 3 6 3 2 1 1;
3 4 5 3 2 1 1;
3 5 4 4 3 1 1;
3 6 3 5 3 1 1;
3 7 3 5 4 1 1;

4 1 6 2 4 1 1;
4 2 6 2 3 1 1;
4 3 5 3 3 1 1;
4 4 4 4 3 1 1;
4 5 3 5 3 1 1;
4 6 2 6 3 1 1;
4 7 2 6 4 1 1;

5 1 5 2 4 1 1;
5 2 5 3 4 1 1;
5 3 4 4 4 1 1;
5 4 3 5 4 1 1;
5 5 3 5 4 1 1;
5 6 2 6 4 1 1;
5 7 2 7 4 1 1;

6 1 5 4 7 1 1;
6 2 4 4 5 1 1;
6 3 3 5 5 1 1;
6 4 2 5 5 1 1;
6 5 2 6 5 1 1;
6 6 2 7 5 1 1;
6 7 1 7 7 1 1;

7 1 4 4 7 1 1;
7 2 4 4 6 1 1;
7 3 2 5 6 1 1;
7 4 2 6 6 1 1;
7 5 2 6 5 1 1;
7 6 1 7 5 1 1;
7 7 1 7 7 1 1];

a=addrule(a,rulelist); %在a中增加模糊推理规则，a为模糊规则库

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_70
a=setfis(a,'DefuzzMethod','centroid'); %Defuzzy 解模糊化采用的是面积重心法（选取
writefis(a,'fuzzpid'); %隶属度函数曲线与横坐标围成面积的重心作为模糊推理的最终输出值）
% save to fuzzy file "fuzz.fis" which can be 保存到模糊文件tank.fis
a=readfis('fuzzpid');%从磁盘装入FIS

figure(1);
plotmf(a,'input',1);%输入模糊集e（偏差隶属度函数）plotmf--绘制给定变量的隶属度函数
figure(2);
plotmf(a,'input',2);%输入模糊集ec（偏差变化率隶属度函数）
figure(3);
plotmf(a,'output',1);%输出模糊集kp（kp隶属度函数）
figure(4);
plotmf(a,'output',2);%输出模糊集ki（ki隶属度函数）
figure(5);
plotmf(a,'output',3);%输出模糊集kd（kd隶属度函数）
figure(6);
plotfis(a);%绘制模糊推理系统FIS对象a

fuzzy fuzzpid;%规则库和隶属度函数的编辑

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_71 刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_72
showrule(a);% Show fuzzy rule base 显示FIS对象a的规则(把分号去掉则会打印出来)
ruleview fuzzpid;%模糊系统的动态仿真

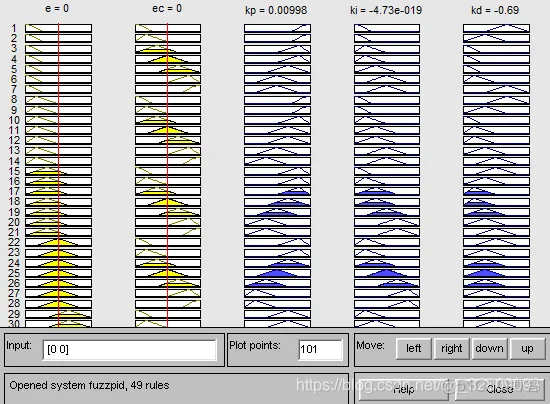
刘金琨智能控制（第2版）仿真实例代码整理_神经网络_73

模糊PID系统程序：chap4_7b.m

%Fuzzy PID Control 模糊PID控制
close all;
clear all;

a=readfis('fuzzpid'); %Load fuzzpid.fis 加载模糊推理系统生成的fuzzpid.fis

ts=0.001; %采样时间为1ms
sys=tf(5.235e005,[1,87.35,1.047e004,0]);%对象传递函数
dsys=c2d(sys,ts,'tustin');%采用Z变换对被控对象进行离散化
[num,den]=tfdata(dsys,'v');

u_1=0.0;u_2=0.0;u_3=0.0;%初始值
y_1=0;y_2=0;y_3=0;

x=[0,0,0]';

e_1=0;
ec_1=0;

kp0=0.40;
kd0=1.0;
ki0=0.0;

for k=1:1:3000
time(k)=k*ts;%运行总时间为3秒

r(k)=sign(sin(2*pi*k*ts)); %输入信号为幅值为1的方波信号
%Using fuzzy inference to tunning PID 利用模糊推理对PID进行整定
k_pid=evalfis([e_1,ec_1],a);
kp(k)=kp0+k_pid(1);
ki(k)=ki0+k_pid(2);
kd(k)=kd0+k_pid(3);
u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);

if k==300 % Adding disturbance(1.0v at time 0.3s) 在0.3s时增加一个干扰
u(k)=u(k)+1.0;
end

y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;
e(k)=r(k)-y(k);
%%%%%%%%%%%%%%Return of PID parameters%%%%%%%%%%%%%%%
u_3=u_2;
u_2=u_1;
u_1=u(k);

y_3=y_2;
y_2=y_1;
y_1=y(k);

x(1)=e(k); % Calculating P
x(2)=e(k)-e_1; % Calculating D
x(3)=x(3)+e(k)*ts; % Calculating I

ec_1=x(2);
e_2=e_1;
e_1=e(k);
end

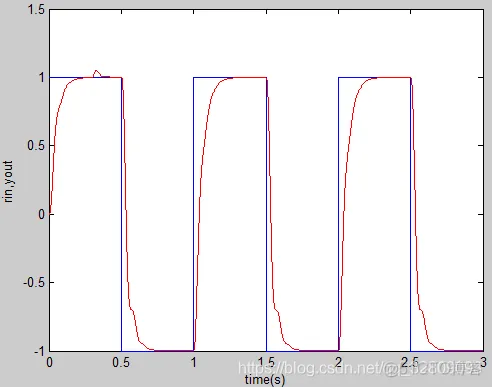
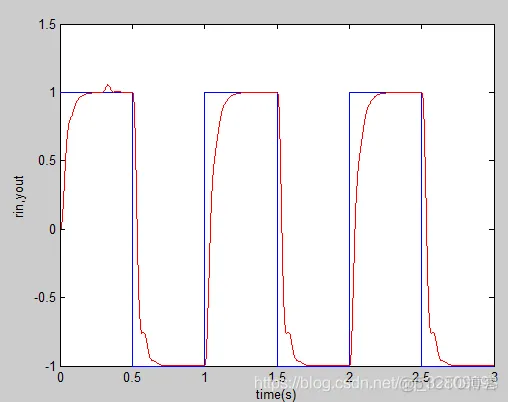
figure(1);
plot(time,r,'b',time,y,'r');
xlabel('time(s)');ylabel('rin,yout');%绘制输入r与输出y响应

刘金琨智能控制（第2版）仿真实例代码整理_模糊控制_74
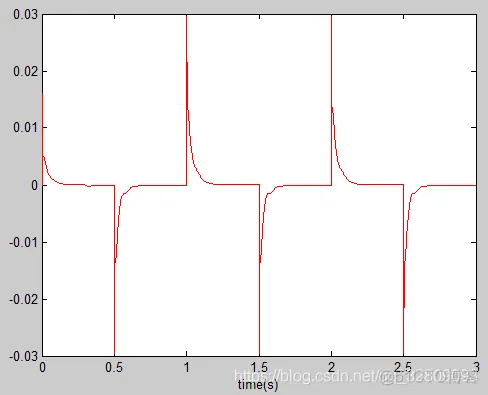
figure(2);
plot(time,e,'r');
xlabel('time(s)');ylabel('error');%绘制控制误差e响应

刘金琨智能控制（第2版）仿真实例代码整理_自适应_75
figure(3);
plot(time,u,'r');
xlabel('time(s)');ylabel('u');%绘制控制量u响应

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_76
figure(4);
plot(time,kp,'r');
xlabel('time(s)');ylabel('kp');%绘制kp自适应整定

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_77
figure(5);
plot(time,ki,'r');
xlabel('time(s)');ylabel('ki');%绘制ki自适应整定

刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_78
figure(6);
plot(time,kd,'r');
xlabel('time(s)');ylabel('kd');%绘制kd自适应整定

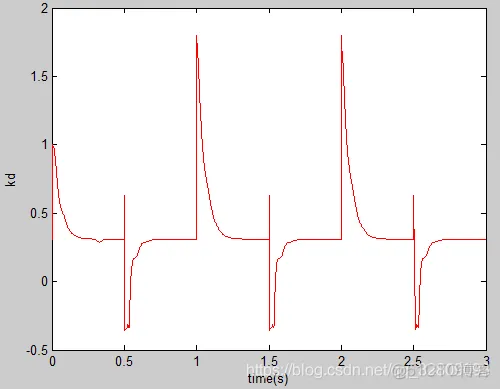
刘金琨智能控制（第2版）仿真实例代码整理_自适应_79

改变初始值Kp=1,Ki=0,Kd=0.5可得

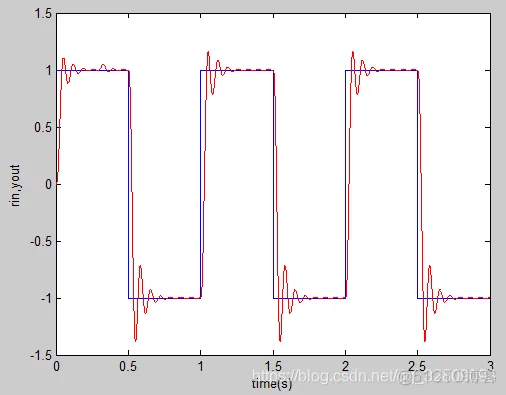
刘金琨智能控制（第2版）仿真实例代码整理_刘军琨_80

改变初始值Kp=0.41,Ki=0,Kd=0.3可得

Ki Kd(可由系统稳定时的值确定初始值)

刘金琨智能控制（第2版）仿真实例代码整理_智能控制_81 刘金琨智能控制（第2版）仿真实例代码整理_智能控制_82

刘金琨智能控制（第2版）仿真实例代码整理_神经网络_83

智能控制全套资料百度云（包括刘军琨编著的智能控制第4版高清PDF、配套书籍的全部仿真程序及PPT、用RBF拟合非线性函数仿真作业及对一个非线性对象使用三种方法的控制仿真大作业（单神经元自适应控制、模糊RBF控制和模糊自适应整定PID控制）的程序及文档整理）请前往我的资源：

javascript:void(0)

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删

返回上级列表

请

联系我们

下一篇: 短波通信系统MATLAB GUI仿真实践（通信视角） >